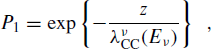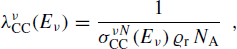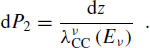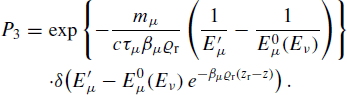Studies on neutrino Earth radiography

Abstract

Neutrino Earth radiography seems to provide an alternative tool to study the very deep geological structures. Even if the level of precision of such measurements might not be very high, nevertheless the information which can be obtained are absolutely independent and complementary to the more conventional seismic studies.

1. Introduction

The Earth’s tomography with ultra-high energy cosmic neutrinos seems to provide a viable independent determination of the Earth’s internal structure (Jain et al., 1999; Reynoso and Sampayo, 2004). Standard methods to measure the density of the Earth are based on seismic wave propagation that have substantial intrinsic uncertainties (Jain et al., 1999).

In this framework, atmospheric neutrinos in the energy range of the order of few TeV provide a unique opportunity to probe the very interior of our planet due to their interaction length which does not exceed too much the Earth radius. In particular, at this energy, neutrinos are copious enough to cross the Earth and interact during their travel transforming in their corresponding charged lepton via Charged-Current Interaction. The detectable events can be classified in two categories: the track events where the charged lepton is produced outside the fiducial volume and is able to emerge from the surface and be detected by the NT, and the contained events, where neutrino converts inside the NT. For seek of brevity we will focus our analysis on track events only.

At the moment the experimental community is undertaking a relevant effort to construct giant Neutrino Telescopes (NT’s). After the first generation of telescopes which has proved the feasibility of the Cerenkov detection technique under deep water (Balkanov et al., 1999) and ice (Ahrens et al., 2002) by detecting atmospheric neutrinos, we are likely approaching the first detections at the IceCube (Ahrens et al., 2004) telescope, being completed at the South Pole, and possibly at the smaller ANTARES (Spurio, 2006) telescope under construction in the Mediterranean. Moreover, ANTARES as well as NESTOR (Aggouras et al., 2006) and NEMO (Migneco et al., 2008) are involved in R&D projects aimed at the construction of a km³ NT in the deep water of the Mediterranean sea, coordinated in the European network KM3NeT (Katz, 2006). In this very exciting scientific framework it has been proposed the idea to use neutrinos, which are elusive particles, to probe the very internal part of the Earth.

In this framework, the evidence for a sensitivity of the physics at a NT to the very deep geological structure is provided by the muons event rate expected at a NT as a function of the arrival direction. It shows a clear angular dependence that is affected by the radial matter density profile adopted, as it is reported in Fig. 1, taken from González-García et al. (2008). In this analysis it is shown the expected zenith angle distribution of atmospheric v _μ induced events in IceCube for different energy thresholds assuming Preliminary Reference Earth Model (PREM) (Dziewonski, 1971). In the following we will refer our calculation to a km³ NT placed at NEMO site, reported in Fig. 2.

Fig. 1

Expected zenith angle distribution of atmospheric v _μ induced events in IceCube for different energy thresholds for PREM is reported (see González-Garcá et al., 2008 for details).

Fig. 2

The surface profile of the area near the NEMO site (red spot) at 36°21′N, 16°10′E. The black curve represents the coast line. The sea plateau depth used in the simulation is 3424 m. The effective volume starts at an height of 100 m from the seabed, to account for the spacing of the first photomultipliers as foresee by the current designs. The km³ detector is oriented along the E-W/S-N directions.

2. Neutrino Sensitivity to Matter Distribution

Neutrino Sensitivity to Matter Distribution In order to understand how the number of charged lepton events at a km³ NT depends on the density of matter crossed by HE neutrinos, let us remind the formalism developed in Cuoco et al. (2007).

We define the km³ NT fiducial volume as that bounded by the six lateral surfaces Σ _a (the subindex a = D, U, S, N, W, and E labels each surface through its orientation: Down, Up, South, North, West, and East), and indicate with Ω _a ≡ (θ _a , φ _a ) the generic direction of a track entering the surface Σ _a . The scheme of the NT fiducial volume and two examples of incoming tracks are shown in Fig. 3. We introduce all relevant quantities with reference to v _μ being the case v_τ completely analogous.

Let dΦ _v /(dE _v dΩ _a ) be the differential flux of UHE v _μ +v̄ _μ . The number per unit time of μ leptons emerging from the Earth surface and entering the NT through Σ _a with energy E _μ is given by

(1)

The kernel k^μ _a (E _v , E _μ ; r⃗ _a , Ω _a ) is the probability that an incoming v _μ crossing the Earth, with energy E _v and direction Ω _a , produces a μ-lepton which enters the NT fiducial volume through the lateral surface dS _a at the position r⃗ _a with energy E _μ (see Fig. 3 for the angle definition). For an isotropic flux we can rewrite Eq. (1), summing over all the surfaces, as

(2)

which defines the total aperture A^μ(E _v ). The contribution of each surface to the total aperture reads

(3)

Fig. 3

The angle definition and the fiducial volume of a km³ NT.

As already shown in details in Cuoco et al. (2007) a typical event corresponds to the simultaneous fulfillment of the following conditions:

• 1) A v _μ with energy E _v travels over a distance z through the Earth before interacting. The corresponding probability P₁ is given by

  

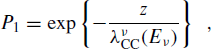  (4)

  where

  

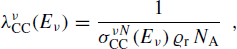  (5)

  where N _A the Avogadro number and ϱ_r is the Earth density assumed to be constant).

• 2) The neutrino produces a μ in the interval z, z + dz, the probability of such an event being

  

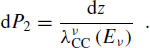  (6)

• 3) The produced μ emerges from the Earth rock with an energy E^′ _μ . This happens with a probability

  

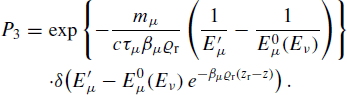  (7)

  See Cuoco et al. (2007) for notations.

• 4) Finally, the μ lepton emerging from the Earth rock propagates in water and enters the NT fiducial volume through the lateral surface Σ _a at the pointr⃗ _a with energy E _μ . The corresponding survival probability is

  

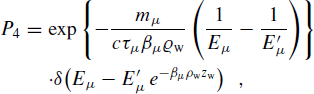  (8)

  where ϱ _w stands for the water density and z _w (r⃗ _a ,Ω _a ) represents the total length in water before arriving to the fiducial volume for a given track entering the lateral surface Σ _a at the point r⃗ _a and with direction Ω _a .

Collecting together the different probabilities in Eqs. (4), (6), (7) and (8), we have

(9)

which once substituted in Eq. (3) provides the total number of events of Eq. (2).

3. Results and Conclusions

As shown the Earth density profile enters via the matter density, ϱ_r in most of the previous expressions, and thus one must expect a certain sensitivity to PREM characteristics of number of events.

In particular we have performed part of the integration contained in Eq. (2) by generating a large number of tracks crossing the NEMO site by means of a detailed DEM of the under-water Earth surface which is available from the Global Relief Data survey (ETOPO2). A grid of altimetry measurements with a vertical resolution of 1 m averaged over cells of 2 minutes of latitude and longitude. In terms of these tracks and applying the above formalism we have reproduced the analogous plot of Fig. 1 in the case on the Mediterranean under sea NT at NEMO site. In fact, in Fig. 4 we report the ratio of the angular distributions of the expected v _μ -induced track events for PREM divided the same quantity obtained for a Homogeneous Earth model. This ratio is evaluated by using two values of the muon energy threshold. A larger threshold amplifies the effect due to the non trivial radial density profile which makes the ratio significantly different from the unit. Unfortunately, increasing the energy threshold also means to reduce the expected number of events and thus the statistics which implies larger error bars.

Fig. 4

The ratio between event rates (PREM over Homogeneous Earth) vs the arrival direction for two different energy thresholds. Here θ denotes the angle between the μ-track and the vertical axis emerging from the Earth surface at detector site.

Nevertheless, as already stated in González-García et al. (2008) the quoted uncertainties, relative to ten years of data taking, seem to suggest the possibility to recognize a non trivial radial density profile with a good level of statistical confidence.