- Article
- Open access
- Published:
Modelling the Earth’s core magnetic field under flow constraints
Earth, Planets and Space volume 62, pages 503–516 (2010)
Abstract
Two recent magnetic field models, GRIMM and xCHAOS, describe core field accelerations with similar behavior up to Spherical Harmonic (SH) degree 5, but which differ significantly for higher degrees. These discrepancies, due to different approaches in smoothing rapid time variations of the core field, have strong implications for the interpretation of the secular variation. Furthermore, the amount of smoothing applied to the highest SH degrees is essentially the modeler’s choice. We therefore investigate new ways of regularizing core magnetic field models. Here we propose to constrain field models to be consistent with the frozen flux induction equation by co-estimating a core magnetic field model and a flow model at the top of the outer core. The flow model is required to have smooth spatial and temporal behavior. The implementation of such constraints and their effects on a magnetic field model built from one year of CHAMP satellite and observatory data, are presented. In particular, it is shown that the chosen constraints are efficient and can be used to build reliable core magnetic field secular variation and acceleration model components.
1. Introduction
Following the launch of the magnetic survey satellites Oersted in 1999, and CHAMP in 2000, a global set of high quality magnetic vector data is now available. Currently, this set spans nearly ten years and has led to time varying models of the core magnetic field of unprecedented accuracy. One of the major achievements is the modeling of the magnetic field Secular Acceleration (SA) i.e. the time evolution of the magnetic field Secular Variation (SV). Indeed, it is crucial to model as accurately as possible the secular acceleration because it has a profound effect on the SV which in turn affects estimates of the liquid outer core flow, just below the Core-Mantle Boundary (CMB). Properly describing the flow at the top of the liquid outer core is essential as it is one key piece of information to understand the dynamics of the core, with implications for other physical process such as long timescale changes in the length of the day.
The secular acceleration is modeled in the available core magnetic field models with time variations described by cubic (or higher order) B-splines. For example this is the case for the CM4 (Sabaka et al., 2004), GUFM (Jackson et al., 2000) or CALS7K (Korte and Constable, 2004) models. However, these models, that are needed to describe relatively long term variations of the Earth’s core magnetic field, have been built with relatively few data per year, and therefore have been strongly smoothed in time.
Extracting the acceleration information from geomagnetic observatory and satellite data is a challenging task. Only recently has it become clear that this is possible for magnetic field models spanning only a few years. First attempts have been made by Lesur et al. (2005), Maus et al. (2005), and Olsen et al. (2005), but their SA models do not agree. The CHAOS model (Olsen et al., 2006) presents a more realistic SA but the use of cubic B-splines to parameterize in time the core magnetic field precludes its continuous mapping. This problem has been addressed in the GRIMM model (Lesur et al., 2008) where order five B-splines have been used, leading to the first continuous time dependent model of the SA that is believed to be reasonably accurate up to Spherical Harmonic (SH) degree 5 or 6. A recent extension of the CHAOS model, named xCHAOS (Olsen and Mandea, 2008, version 03c-08, personal communication), although built using completely different data selection techniques, has SA agreeing with the very long spatial wavelengths of that computed from GRIMM. Typically, the two models present strong similarities in SA up to SH degrees 4 or 5. For higher SH degrees however, the two SA models are radically different (see Fig. 1). The data set and the applied processing do not resolve the acceleration signal well and there is not even agreement as to what the shape of the SA power spectrum should be. Usually, during the modeling process, the SA is controlled through a rather simple regularization imposing smooth behavior in space and time. Indeed, it is rather difficult to estimate what smoothness or magnitude the SA should have. Therefore, it is necessary to seek for alternative ways of regularizing the magnetic field models in order to improve our understanding of the SA at SH degrees higher than 5.
In this manuscript we present our approach to model both the core magnetic field and the flow on the core surface simultaneously. More specifically, a core magnetic field model, built to fit a magnetic data set, is co-estimated together with a flow model using the radial diffusionless induction equation (hereafter the FF-equation). Constraints are applied exclusively on the flow model in order to obtain the best possible core field model. At a glance, it is not obvious why smoothing the flow is preferable to smoothing the field. Both regularization techniques are, however, likely to single out a possible mechanism (i.e. diffusion or advection) for the SV generation in the core. Here, by using the FF-equation we favor an advective process, and show that smoothing in time the field is likely to favor diffusion. Indeed, it is well-known that some diffusion must exist, and therefore an advective process, even if dominant, cannot be the exclusive source of the SV. To avoid this pitfall, we impose the diffusionless hypothesis (hereafter the FF-hypothesis) in a weak form, such that the data set can always be properly fitted.
The idea of imposing the FF-hypothesis on a core field model has already been used for example by Bloxham and Gubbins (1986) and Jackson et al. (2007). These authors require the magnetic flux to be constant in time over areas on the CMB defined by null flux curves at different epochs. Our approach is different because we co-estimate the flow and the field and therefore impose some constraints on the flow. Furthermore, the FF-hypothesis is applied continuously in time. Closer to our approach is that of Waddington et al. (1995) where observatory data are fit by parameterizing the flow on the core surface. Their work is sometimes seen as an early attempt of a data assimilation technique where the physical model for the flow evolution is replaced by an hypothesis of steady flow. Beggan and Whaler (2009) also used a steady flow model, combined with Kalman filtering, to forecast change of the magnetic core field. In our case the flow is allowed to vary in time and the difference with assimilation techniques is that evolution equations for the flow are not introduced. On the other hand, the new assimilation techniques recently developed for the magnetic field modeling are not yet based on real data but only on models (Fournier et al., 2007; Liu et al., 2007). We also note that the approach we follow in this study has been independently suggested, in their conclusion, by Whaler and Holme (2007).
Here, our main goal is to investigate how well one can control a core field model by applying constraints on the co-estimated flow model. The methodology is tested on a vector CHAMP satellite and observatory data set spanning only one year. By using such a short time span, we make sure that the constraints applied on the flow have an obvious effect on the field model. On the other hand, the resulting core field model cannot be of the same quality as models recently derived from the full set of available satellite and observatory data, such as GRIMM (Lesur et al., 2008) and xCHAOS (Olsen and Mandea, 2008). In particular, as for other models built from short time span data sets (see for example Olsen, 2002), the acceleration cannot be accurately modeled. We also impose some strong restrictions on the flow by first truncating the flow model to a relatively low SH degree, and second, choosing the same temporal representation for the flow coefficients and for the Gauss coefficients. As for the field models, the obtained flow model cannot be of the same quality of recently published models, nevertheless, it is of sufficient quality for the purpose of this study.
The manuscript is organized as follow. The necessary assumptions of the problem and the implementation details are presented in the next section. In the third section the application to the CHAMP satellite and observatory vector data is presented. The fourth section is dedicated to evaluating the effect of the regularization on the field and flow models. Finally, in the fifth section, the obtained magnetic field, the fit to the data, and the flow models are discussed and compared with the GRIMM magnetic field model.
2. Theoretical Background
Let us first consider a (column) vector d made of N vector magnetic field measurements d i at (t i , θ i , ϕ i , r i ) where t, θ, ϕ and r are the time, co-latitude, longitude and radius respectively and i = 1, 2, …, N. For simplicity, we assume in this section that only the core field contributes to these measurements. These measurements are made above the Earth’s surface and are contaminated by some noise. The Earth’s surface is away from the core magnetic field sources and therefore the observations can be well approximated by a field model B(t, θ, ϕ, r) that is the negative gradient of a potential, itself solution of the Laplace’s equation:


To derive a flow model at the core surface, we neglect the effect of mantle conductivity on a temporal variation of the core field, and therefore assume that the core field model determined at the observation radius can be directly downward continued to the CMB. Further it is assumed that the contributions to the temporal variations of the core field ∂ t B are first the advection of the magnetic field line of force by the liquid outer core flow and second the diffusion of the field. Following Roberts and Scott (1965) (see also Holme, 2007) we write:

where U is the flow in the liquid outer core. In this equation the parameter  is proportional to the inverse of the core conductivity and is therefore very small. As a consequence, for SV on decadal time scales and processes on large spatial scales (> 103 km) the second term on the right hand side of Eq. (3) can be neglected. This approximation is called the Frozen-Flux hypothesis (i.e. FF-hypothesis, see Roberts and Scott, 1965 for the original justification of this approximation). Under this approximation, and assuming that the CMB is a spherical surface, the radial component of Eq. (3) becomes the radial diffusionless induction equation (i.e. the FF-equation):
is proportional to the inverse of the core conductivity and is therefore very small. As a consequence, for SV on decadal time scales and processes on large spatial scales (> 103 km) the second term on the right hand side of Eq. (3) can be neglected. This approximation is called the Frozen-Flux hypothesis (i.e. FF-hypothesis, see Roberts and Scott, 1965 for the original justification of this approximation). Under this approximation, and assuming that the CMB is a spherical surface, the radial component of Eq. (3) becomes the radial diffusionless induction equation (i.e. the FF-equation):

where U
h
is the vector flow tangential to the spherical surface on the top of the core (the radial flow component necessarily vanishes at the core surface), B
r
and ∂
t
B
r
are the radial component of the core field model and its SV at the CMB and  is the tangential gradient on the sphere. The tangential components of the magnetic field are discontinuous across the CMB and therefore are not used here to derive the core flow (Jault and Le Mouël, 1991).
is the tangential gradient on the sphere. The tangential components of the magnetic field are discontinuous across the CMB and therefore are not used here to derive the core flow (Jault and Le Mouël, 1991).
2.1 The discrete problem
At the CMB, the magnetic field model solution of Eqs. (1) and (2) can be parameterized using SHs:


where c = 4385 km is the Earth’s core reference radius,  are the Schmidt semi-normalized SHs. We use the convention that negative orders, m < 0, are associated with sin(|m|ϕ) terms whereas null or positive orders, m ≥ 0, are associated with cos(mϕ) terms. The N
t
basis functions in time ψ
i
(t) are polynomials of maximum degree N
t
− 1. The sum in the right hand side of Eq. (5) goes up to degree L
B
and therefore the magnetic field model is defined by (L
B
(L
B
+ 2)N
t
) Gauss coefficients
are the Schmidt semi-normalized SHs. We use the convention that negative orders, m < 0, are associated with sin(|m|ϕ) terms whereas null or positive orders, m ≥ 0, are associated with cos(mϕ) terms. The N
t
basis functions in time ψ
i
(t) are polynomials of maximum degree N
t
− 1. The sum in the right hand side of Eq. (5) goes up to degree L
B
and therefore the magnetic field model is defined by (L
B
(L
B
+ 2)N
t
) Gauss coefficients  These Gauss coefficients can be estimated by solving the linear system:
These Gauss coefficients can be estimated by solving the linear system:

where the elements of the N × (L
B
(L
B
+ 2)N
t
) matrix A are derived from Eqs. (5) and (6) and  is the vector of Gauss coefficients. The vector e
d
is introduced to account for the noise in the data. We recall that N is the number of data values. In the present study L
B
= 14 and N
t
= 5.
is the vector of Gauss coefficients. The vector e
d
is introduced to account for the noise in the data. We recall that N is the number of data values. In the present study L
B
= 14 and N
t
= 5.
In order to re-write Eq. (4) as a set of linear equations, the usual parameterization of the flow at the core surface is used (see for example Whaler, 1986; Bloxham, 1988). The flow at the core surface is described as the sum of poloidal and toroidal flows, each of these flows being parameterized using SHs:



Here we note that the same basis functions are used to expand the magnetic field model and the flow model in time.
The radial component of the core magnetic field model is given by:

Inserting Eqs. (8) and (11) into Eq. (4), then multiplying both sides by  and finally integrating over the sphere leads to:
and finally integrating over the sphere leads to:

where  and
and  are the Gaunt and Elsasser’s integrals respectively.
are the Gaunt and Elsasser’s integrals respectively.

We de fine the matrix Ψ(t) made of the ∂ t ψ i (t) and padded with zeros such that:

The number of elements of this vector is  where L
B
and L
F
are the upper-bounds of the summations in Eqs. (5) and (9). This number corresponds to the Gaunt and Elsasser’s integral exclusion rule (see for example Moon, 1979), and the matrix formulation for Eq. (12) becomes:
where L
B
and L
F
are the upper-bounds of the summations in Eqs. (5) and (9). This number corresponds to the Gaunt and Elsasser’s integral exclusion rule (see for example Moon, 1979), and the matrix formulation for Eq. (12) becomes:

The elements of the time-dependent matrice A
g
(t) are derived from Eq. (12) and the truncation error e
t
is introduced because  is known only up to SH degree L
B
leading to only L
B
(L
B
+ 2) non-zero elements in the vector Ψ(t) · g. The dimension of vector u is 2L
F
(L
F
+ 2)N
t
. This is also the number of columns of A
g
(t). In this work we set L
B
= L
F
= 14.
is known only up to SH degree L
B
leading to only L
B
(L
B
+ 2) non-zero elements in the vector Ψ(t) · g. The dimension of vector u is 2L
F
(L
F
+ 2)N
t
. This is also the number of columns of A
g
(t). In this work we set L
B
= L
F
= 14.
An alternative way of presenting Eqs. (12) and (15) is to define the matrix A u (t) such that A g (t) · u = A u (t) · g and then Eqs. (12) and (15) become:

As for A
g
(t), the A
u
(t) matrix elements are derived from Eq. (12). The matrix A
u
(t) has only L
B
(L
B
+ 2) N
t
columns but the same number of rows as A
g
(t). We have verified that for non-vanishing flow the matrix  is not singular, therefore if e
t
= 0, the only solution of Eq. (16) is the trivial solution g = 0. This is clearly in contradiction with the solution of Eq. (7) and comes from the fact that the parameterization (5), (6), (9) and (10), for the core field and for the flow respectively, are not compatible with the FF-equation (4). This inconsistency has also been pointed out by Bloxham (1988). Elements of the proof are given in the appendix, and we simply note here that a small “representation ”error e
r
should be considered for both Eqs. (15) and (16). The relative importance of e
t
and e
r
is discussed in Subsection 2.3.
is not singular, therefore if e
t
= 0, the only solution of Eq. (16) is the trivial solution g = 0. This is clearly in contradiction with the solution of Eq. (7) and comes from the fact that the parameterization (5), (6), (9) and (10), for the core field and for the flow respectively, are not compatible with the FF-equation (4). This inconsistency has also been pointed out by Bloxham (1988). Elements of the proof are given in the appendix, and we simply note here that a small “representation ”error e
r
should be considered for both Eqs. (15) and (16). The relative importance of e
t
and e
r
is discussed in Subsection 2.3.
2.2 Solving for the Gauss coefficients
To model the core magnetic field alone from a data set, the Gauss coefficients defined in Eq. (5) have to be estimated from the discrete linear system (7). This linear system is usually over-determined and therefore solved by least squares i.e. the vector g is estimated such that it minimizes the functional Φ0 defined by:

where the superscript T denotes the transpose and the matrix Wd is a matrix of weights that is described in the next subsection (2.3).
In order to co-estimate the core field and flow models, the linear systems (7) and (15) are solved simultaneously. The set of Gauss and flow coefficients solutions of Eqs. (7) and (15) are obtained by least squares i.e. the Gauss and flow coefficients  are estimated such that they minimize the functional Φ defined by:
are estimated such that they minimize the functional Φ defined by:

where λ1 is a scalar parameter that has to be adjusted and Φ0 is defined in Eq. (17). If the elements of the diagonal weight matrix Wġ are defined by  , then the functional Φ1 is the discrete equivalent of the integral:
, then the functional Φ1 is the discrete equivalent of the integral:

However, in this work, the elements of Wġ have a more complex dependence on the SH degree. Their derivation is described in the next sub-section 2.3. In Eq. (18), the summation in ¦1 is the integration over time. The sampling points t
i
and the associated weights  are those of Gaussian integration rules and are such that the products of the different time-dependent terms are integrated exactly over the time span of the core field model
are those of Gaussian integration rules and are such that the products of the different time-dependent terms are integrated exactly over the time span of the core field model  .
.
Because A
g
(t
i
) in the functional Φ1 depends on the Gauss coefficients  and is multiplied by u, this optimization problem is clearly non-linear. We therefore re-write Eq. (18) explicitly as an iterative process. Consider u
k
and g
k
, the kth estimates of the solution u and g respectively. Let us call A
uk
(t) and A
gk
(t) their corresponding matrices. We want to estimate δu and δg that minimize:
and is multiplied by u, this optimization problem is clearly non-linear. We therefore re-write Eq. (18) explicitly as an iterative process. Consider u
k
and g
k
, the kth estimates of the solution u and g respectively. Let us call A
uk
(t) and A
gk
(t) their corresponding matrices. We want to estimate δu and δg that minimize:

where  and
and  This optimization problem, that is now linear in δu and δg, can be solved but the iterative process is unlikely to converge unless some constraints are applied on the flow model. Indeed, it is well known that the problem is ill-posed for the flow (Holme, 2007). For example, if L
F
e L
B
, it is always possible to define an average toroidal flow following the iso-contours of the average radial component of the core field model. Such a flow does not generate any SV by advection. In order to obtain the best possible magnetic field model fitting the data and simultaneously reducing the null space for the flow, two types of constraints are considered:
This optimization problem, that is now linear in δu and δg, can be solved but the iterative process is unlikely to converge unless some constraints are applied on the flow model. Indeed, it is well known that the problem is ill-posed for the flow (Holme, 2007). For example, if L
F
e L
B
, it is always possible to define an average toroidal flow following the iso-contours of the average radial component of the core field model. Such a flow does not generate any SV by advection. In order to obtain the best possible magnetic field model fitting the data and simultaneously reducing the null space for the flow, two types of constraints are considered:
-
-|First, the flow model can be forced to have a convergent spectrum. The flow is then required to minimize Bloxham’s “strong norm ”(Bloxham, 1988; Jackson, 1997),
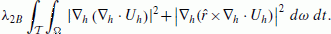 (21)
(21)Another option is to minimize a weaker norm (Gillet et al., 2009),
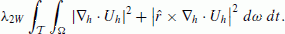 (22)
(22)The first and second terms in the integral (22) measure the amount of up/downwelling and the radial vorticity respectively. The damping parameters λ2B and λ2W controls to what extent the flow follows these constraints.
-
-|Second the flow model is chosen such that it varies smoothly in time, namely:
 (23)
(23)where λ3 is the associated damping parameter and
 denotes the flow time derivative. We expect such a constraint to efficiently regularize the inverse problem as in the limit of a constant flow there is a unique flow solution of the FF-equation (Voorhies and Backus, 1985). We also expect that minimizing Eq. (23) constrains efficiently the secular acceleration.
denotes the flow time derivative. We expect such a constraint to efficiently regularize the inverse problem as in the limit of a constant flow there is a unique flow solution of the FF-equation (Voorhies and Backus, 1985). We also expect that minimizing Eq. (23) constrains efficiently the secular acceleration.
2.3 Errors and weight matrices
In the inverse problem (17), that consists of estimating a core field model from a data set, the weight matrix Wd depends, at first, on the estimated data accuracy and also on the data density. The matrix is then updated during the iterative least squares inversion process used to derive the model. The data errors are assumed to be uncorrelated so the weight matrix is diagonal.
When the field and the flow are co-estimated, the functional Φ1 and the diagonal weight matrix Wġ are introduced (Eq. (18)). The Wġ matrix elements result from three different contributions, namely: the surface integration weights in Eq. (19), the representation errors e r and the truncation errors e t (see Subsection 2.1 for these error definitions).
At a given instant t i , the integral over the CMB of the squared radial component of the SV is given by:

where the Gauss’ coefficients are defined at the CMB (see Eqs. (5) and (6)). Accordingly, integration weights for a given SH degree l are:

For SH degrees less than or equal to L B , we assume that the representation error e r dominates the truncation error e t . This latter error is simply ignored (but see the remark at the end of the sub-section). We set the variance at SH degree l of the representation errors proportional to:

where  is the estimated power spectrum of a SV model defined at the CMB. This corresponds to the idea that the representation errors at CMB are simply proportional to the SV Gauss coefficients.
is the estimated power spectrum of a SV model defined at the CMB. This corresponds to the idea that the representation errors at CMB are simply proportional to the SV Gauss coefficients.
For SH degrees larger than L B , the SV model is undefined giving rise to the truncation errors e t . The representation error e r is then ignored. At the observational radius a = 6371.2 km, the power spectrum of the SV at SH degrees larger than L B is smaller than 0.5 (nT/y)2. We use this upper-bound as an estimate of the truncation error variance at SH degree l:

This variance is clearly over-estimated which, in the inverse problem defined by Eq. (18), is nearly equivalent to neglecting all equations above SH degrees L B in the linearsystems (15)and(16).
The elements of the diagonal weight matrix Wġ that correspond to the Gauss coefficients of SH degree l ≤ L B , are therefore given by:

for a SH degree l > L B the weights are given by:

Usually, when a flow model is derived from a given core field model, two other types of errors are considered:
-
Observational errors that account for the errors in the Gauss coefficients estimated through the optimization process defined by Eq. (17).
-
A second type of truncation error to account for the fact that short wavelengths of the magnetic field can interact with the short wavelengths of the flow to generate long wavelength secular variation (Eymin and Hulot, 2005).
In the present work, observational errors are not considered because the field and the flow are co-estimated. The second type of truncation errors is also omitted but, in return, we have to impose a rapidly converging spectrum onto the flow. This is not ideal, but it is necessary at this stage, as the field model cannot be efficiently constrained if the flow model has too many degrees of freedom.
3. Application to CHAMP and Observatory Data
The methodology described in the previous section has been implemented and applied to a vector data set provided by the CHAMP satellite and 137 observatories. The data set spans approximately one year from 2004.87 to 2005.94 and has been selected using exactly the same selection criteria as for the GRIMM field model (Lesur et al., 2008). These can be summarized as:
-
Only vector data are used.
-
The data are selected for quiet magnetic conditions.
-
High-latitude three component vector data are selected at all local times.
-
Mid- and low-latitude data are selected along the X and Y Solar Magnetic (SM) directions during night times.
With such a selection process the data set combines 35975 X and Y (SM) satellite data at mid and low latitudes, 65147 satellite vector data over polar regions, 38954 X and Y (SM) observatory data at mid and low latitudes, and finally 13974 observatory vector data at high latitudes. Gaps in the satellite data distribution are seen at high latitudes due to the blinding of one of the CHAMP star cameras by the sun, whereas at mid and low latitudes they are due to the local time selection applied to minimize the contribution of the ionospheric field in vector data. Observatory data present no gaps over the time period.
The magnetic field contributions modeled are similar to those in GRIMM. The core field model (see Eqs. (5) and (6)) is parameterized using SH up to degree 14 and an order 4 polynomial in time (i.e. this is equivalent to order 5 B-splines in between two spline knots). A static internal field is modeled up to SH degree 20, which is enough to avoid aliasing effects in the core field model. The large scale external field is modeled only at SH degree 1, but the modeling is robust only in the X and Y SM directions due to the data selection at mid and low latitudes. As in GRIMM, the time variations of this large scale external field are parameterized using a piecewise linear polynomial in time with a node every three months. The rapid time variations are parameterized using the VMD (time series of the estimated disturbances due to large scale external fields (Thomson and Lesur, 2007)). Crustal offsets are co-estimated for observatory data in order to account for the unknown contributions from the lithosphere. The high latitude ionosphere field or the toroidal field generated by Field Aligned Currents (FAC) are not considered in the modeling. Again further details can be found in Lesur et al. (2008).
The model parameters are estimated by fitting the data set, either in the least squares sense (i.e. using an L2 measure of the misfit to the data), or using a reweighted least squares algorithm and an L1 measure of the misfit to the data (Farquharson and Oldenburgh, 1998). With the data set spanning only one year, the model parameterization described above is much too complex to be derived without regularization, but it is well suited to test how the constraints applied to the flow affect the field model. Several types of constraints are introduced:
-
A model is built (hereafter the USN-model) using the usual approach that consists of minimizing simultaneously the data misfit and a measure of the model roughness in time at the CMB. Here we use:
 (30)
(30)where λ1U and λ2U have to be adjusted in order to build a realistic model.
-
Two further series of models are built using the approach described in the previous section. They differ by the measure used to minimize the flow complexity in space: either Eq. (21) (hereafter the BSN-model series) or Eq. (22) (hereafter the WSN-model series). In both models, Eq. (23) is minimized to guarantee temporal smoothness of the flow.
4. Effect of the Regularization on the Co-estimated Field and Flow Models
In this section we compare and discuss the choice of regularization for the co-estimation of the core magnetic field and flow models. All results presented in this section are for the BSN models and are obtained using an L2 measure of the data misfit. This measure does not lead to the best solutions but is sufficient to understand the response of the model solutions to the constraints applied to the inversion process. The results obtained using an L1 measure of the misfit require much longer computation time, and are therefore derived only for a limited small set of damping parameters. Such results are presented in the next section.
As noted before, even if the data set consists only of magnetic vector components, the inverse problem for the BSN models is non-linear due to the co-estimation of the core and flow models. An initial guess is therefore required. This initial guess is built from the USN-model and an associated flow model derived through a standard flow inversion using Eq. (15). The solution of the iterative process is accepted when two successive models of the flow are not significantly different. Such a stable solution is obtained in less than twenty iterations and the final solution is close enough to the starting models for no local-minima to be observed. When started too far from the final solution, we observe that the iterative process simply diverges. In this work we expect the core field model to be a solution of the FF-equation, i.e. the damping parameter λ1 in Eq. (20) is set to a relatively large value λ1 = 10−3. To estimate quantitatively how well the derived model respects the FF-hypothesis we define the dimensionless ratio ϱ by:

where Φ1 is defined in Eq. (18) and the denominator is just the same quantity Φ1 derived for a null flow vector u.By testing different models, we observed that for models parameterized with order 4 polynomials in time and spanning only one year, any value of ϱ smaller than 10−9 correspond to models in good agreement with the FF-hypothesis
We consider first the effect of minimizing the complexity of the flow at relatively high spherical harmonic degrees. This is achieved by setting the λ2B value in Eq. (21), successively to 10−3.5,10−3,10−2.5,10−2.25,10−2 and 10−1.5. The value of λ3 in Eq. (23) is set to the ad hoc value 104.25. The resulting power spectra of the SV at the CMB for year 2005.4 are plotted in Fig. 2 for all these λ2B values. As the data set spans only one year, and because only the L2 norm solution is calculated, the SV is resolved robustly only up to the SH degree 9. However, it is clear that the variation of λ2B affects all the higher SH degrees of the spectra. This is in contrast with the static core field that is not significantly affected by the smoothing constraint. Therefore, as a consequence of imposing the FF-approximation, constraining the flow to get a convergent spectrum directly affects the SV as long as the static part of the core field model is robustly estimated.
Left: Evolution of the SV-BSN spectrum at the core-mantle boundary depending on the damping parameter value: λ2B = 10d. Right: Trade-off curve between a measure of the SV energy and a measure of the misfit to the data. The labels on the points give the corresponding values of the damping parameter: λ2B = 10d.
Figure 3 presents the evolution of the power spectrum of the toroidal and poloidal flows as a function of the λ2B values. The chosen value has to be larger than or equal to 10−3 for the flow to present a clearly converging spectrum. The value λ2B = 10−1.5 is too large and leads to a significant increase in the misfit to the data. Discriminating between the three remaining acceptable λ2B values is rather difficult. We choose here the value λ2B = 10−2.25. For this value, the spectra of the toroidal and poloidal flows are convergent and the model is compatible with the FF-hypothesis (ϱ = 0.410−15). The convergence of the spectrum is fast enough for the possible contributions to the large scale SV of the magnetic field advected by the small scale flow to be very small. This value is also close to the knee of the tradeoff curve of SV energy versus data misfit (Fig. 2, right). On a data set spanning several years, the SV can be more robustly defined and it is then expected that the regularization affects only the SV for the first and last six months of the model time span.
We now keep the damping parameter λ2B in Eq. (21) at the value 10−2.25 and control the changes of the flow in time by varying the parameter λ3 between 103.5 to 106. We note that the time variations of the flow are of much smaller amplitude than the flow itself. Therefore, adjusting the damping parameter λ3 does not affect significantly the flow nor the SV estimates, and the damping parameter λ2B needs no further modifications. Figure 4 gives the power spectra of the static part of the core magnetic field (CF), its SV and its acceleration (SA), for year 2005.4. The spectra are calculated at the Earth’s reference radius α = 6371.2km and for several values of the damping parameter λ3 = 10d. The curves for the static core field and its SV are given for d = 4.25 only, as the power spectra are nearly the same for all the other damping parameter values. The acceleration however changes significantly with λ3.
Left: Evolution of the power spectra of the static part of the core magnetic field (CF), its SV and its acceleration (SA) for different values of the damping parameter: λ3 = 10d. The estimated power spectrum of the background acceleration (BSA) is shown by the solid line. The power spectra are calculated for year 2005.4 at the Earth’s reference radius. Right: Trade-off curve between the SA energy and a measure of the misfit to the data. The labels on the points give the corresponding values of the damping parameter: λ3 = 10d.
In order to understand the behavior of the SA, one has to differentiate in time the radial diffusionless induction Eq. (4). This leads to:

In the two terms on the Right Hand Side (RHS) of Eq. (32), we observe that the first strongly dominates the second at the Earth’s reference radius. Although the flow amplitude is much larger than its variation in time, this does not balance the difference in amplitude between the magnetic field and its SV. In other words, it is the flow time variations that control most of the magnetic field acceleration. The SV in the second term on the RHS of Eq. (32) can be replaced by its expression (4), leading to:

Obviously, this second term depends only on the field and the flow. Therefore by defining the flow model and imposing the FF-hypothesis, a “background ”SA is defined by the second term on the RHS of Eq. (33), that does not directly depend on the flow temporal variations. A question arises regarding how well this background SA is estimated by the truncated models of the field and the flow derived through the inversion process. To discuss this, two possible effects should be considered:
-
1)
The unknown short wavelengths of the flow and SV can interact to contribute to the large wavelength of the SA. The spectrum of the modeled SV is not convergent at the CMB and therefore this truncation error for the background SA is likely to be significant. However, as for the advection of the short wavelengths of the field by the short wavelengths of the flow, we do not expect this effect to be dominant at small SH degrees. Again, this holds because our flow is essentially large scale and has a convergent spectrum.
-
2)
The flow resolved by the inversion process is only part of the true flow because when advecting the field lines, part of the flow does not contribute to the SV. This hidden flow can nevertheless contribute to the background SA. If we accept the common consensus that the strength of this hidden flow is at most of the same order of magnitude as the modeled flow (see for example Rau et al. (2000) or Asari et al. (2009)), then we can assume that the interaction of the SV with the hidden flow is not larger than the interaction with the modeled flow. Overall, our estimated background SA may not be accurate, but the order of magnitude is acceptable. The power spectrum of the estimated background SA is shown in Fig. 4.
It is unlikely that the flow temporal variations are organized such that their associated SA systematically cancels the background SA. Furthermore, the rapidity of the SA evolution, as estimated in core field models like GRIMM and xCHAOS from the energy in their third time derivative, suggests that the flow and its time variations have very different time scales. Therefore, the first and second terms on the RHS of Eq. (32) are likely to be decoupled. We therefore suggest that, in Fig. 4, the power spectrum associated with the background SA defines a lower limit of the SA spectrum for a core field compatible with the FF-hypothesis. This is important because it gives us a criterium to test the compatibility of a model with the FF-hypothesis: A core field model with a very steeply decreasing SA spectrum is unlikely to be compatible with the FF-hypothesis.
By strongly damping the flow time variations one may try to reach the limit where only the background SA is significant. This limit was not reached at low SH degrees even for our largest damping value λ3 = 106 (not shown). At higher SH degrees (i.e. from degree 10 and above) the spectra do not change significantly with the damping value and obviously the solutions get closer to this limit. This difference in behavior depending on the SH degree is simply due to the fact that the data set used does not resolve well the acceleration at high SH degrees.
The plots in Fig. 5 show the evolution of the flow time variation spectra as a function of the applied damping. Again, because only one year of data are used, it is relatively difficult to estimate what the best damping parameter value is as the RMS misfit is little affected by a variation of λ3. We choose here λ3 = 104.25 for the SA energy at small SH degrees to be of the same order as those of the GRIMM and xCHAOS models. This corresponds in Fig. 4 right, to a value fairly close to the knee of the damping curve. For the largest damping parameter values (λ3 > 105), the misfitto data starts to increase significantly. This confirms that some time variations of the flow are needed to fit the SV data.
5. Results and Discussions
In this section we present and compare the results obtained using different regularization techniques. All these results were obtained using a L1 measure of the misfit. The number of iterations before reaching a stable solution is relatively large for such models and data sets: 20 iterations for the USN model and up to 60 iterations for the BSN or WSN models (for the definition of these models refer to Section 3).
The USN-model is derived using the regularization parameter λ1U = 10−4.5 and λ2U = 10−025 in Eq. (30). It is relatively difficult to set these damping parameter values by examining the trade-off between the fit to the data and the roughness of the solution. We therefore simply set these values such that the power spectra of the model solution, secular variation and acceleration stay reasonably close to those of the GRIMM model. The BSN and WSN models are derived as described in Section 4 and the chosen damping parameter values are λ1 = 10−3, λ3 = 104.25 for both models and λ2B = 10−2.25, λ2W = 10−05 for BSN and WSN respectively (see Eqs. (21), (22), and (23)). The data misfits for these three models are given in Table 1 together with the number of data. For all three models, the fit to the data is good at mid and low latitudes but degrades closer to the poles. This is to be expected, because of the chosen data selection criteria. For comparison Table 1 also gives the fit to the same satellite data set for the GRIMM model with its lithospheric component truncated at SH degree 20. Not surprisingly, at mid and low latitudes the fit for the GRIMM model is slightly worse than for the other three models, because it was built on much larger time span data set.
In Fig. 6, the power spectra of the static core field (CF), SV and SA for the four models GRIMM, BSN, USN, WSN, are compared. All these power spectra are calculated at the Earth’s reference radius a = 6371.2 km and for year 2005.4. All four models have a static part (CF) with very similar power spectra. These cannot be distinguished and only the GRIMM model is displayed.
The GRIMM model presents a SV with slightly less power from SH degrees 6 to 8, explained by the fact that GRIMM is built on a different data set and is smoothed in time. SV-BSN and SV-WSN models are essentially the same. They have very similar power spectra and the power spectrum of their differences never exceeds 0.08 (nT/yr)2. Similarly, the power spectrum of the differences between the SV-BSN (or SV-WSN) model and the associated SV estimated through the FF-equation (i.e. the SV generated exclusively from the advection of the field lines by the flow) never exceeds 5.0 10−10 (nT/yr)2 in 2005.4. The ratio ϱ, defined in Eq. (31), is 0.919−15 for the BSN model and 0.219−14 for the WSN model. Therefore, the models built follow (not exactly but very closely) the FF-hypothesis. As expected, due to the regularization technique employed, these two SV models can be downward continued to the CMB without further regularization. The SV-USN model is clearly dominated by the regularization above SH degree 10. Its power drops excessively rapidly from SH degrees 11 to 14.
Figure 7 displays the vertical down component of the SV at the CMB (c = 3485 km) for both the GRIMM and BSN models. The GRIMM model is truncated at SH degree 12 because, for higher degrees, it contains signal that cannot be attributed to the core. BSN presents stronger SV in some areas. By experimenting with different truncation degrees, we observed that under Asia and Indian ocean, this is due to the SH truncation degree, whereas under Africa and Antarctica it may be attributed to the slightly better fit to the data set. Under western Atlantic at mid latitudes, the SV power in GRIMM has slightly shifted to higher degrees in BSN. Around the Northern Pole, the GRIMM characteristic alternating positive and negative SV patches along longitudes are slightly more pronounced in BSN. This is partially due to the higher truncation SH degree, but is also enhanced by the regularization process. Because of the core static field shape in these area, such patterns can be easily explained by a flow circulating around the pole that advects the field lines. It is remarkable that the SV for BSN (and WSN) does not present obvious spurious patterns. In particular East-West oscillations near the dip equator, similar to the well known Backus effect, are not present as is generally the case for high spherical harmonic SV models (Wardinski et al., 2008).
The SA models power spectra, in Fig. 6, are significantly different. As described above, the damping parameter values of the BSN, USN, WSN models have been adjusted such that all SA power spectra match around SH degree 1. From there, the SA-BSN and SA-WSN power spectra stay more or less constant up to SH degree 3 and then drop regularly down. As discussed in Section 4, the SA-BSN and SA-WSN power spectra presented here for SH degree higher than 8, are the lowest possible for the models to be compatible with the FF-hypothesis. The behavior of the SA-USN model is clearly anomalous and it shows that the selected data set over a single year does not resolve well the acceleration. It is also clear that the integrals defined in Eq. (30) impose constraints on the high SH degree of the SA-USN model that are too strong, leading to an unrealistic decrease in the spectrum. Such a model is not compatible with the FF-hypothesis (see discussion in Section 4). We see immediately the effect of using the new approach for regularizing the magnetic field inversion process: the time behavior of the field model is consistent with the underlying physical process described by the FF-equation and advection is favored as a possible source of the SV. The spectrum of the SA for GRIMM is above the others for degrees 3 to 9. This does not necessarily mean that this spectrum is too high. As stated above, one year of data is not enough to resolve well the SA and by accumulating data over several years, the spectra from both the BSN and WSN model accelerations would possibly rise. However, above SH degree 9 the GRIMM SA is controlled by the applied regularization and probably drops too rapidly to be consistent with the FF-hypothesis.
The SA obtained through our inversion process is only valid for the first two or three SH degrees. Most of the SA patterns observed in the GRIMM model correspond to the SH degree 4 or 5. These SH degrees are not resolved here. We observe however, that the BSN and WSN SA models can be downward continued to the CMB without further regularization. There, they are dominated by their short wavelengths, and the patterns, mainly controlled by the FF-equation, are associated with strong gradients of the SV model (maps of the SA are not shown here).
Figure 8 shows the power spectra of the toroidal and poloidal flows from the BSN and WSN models and also the power spectra of the flow temporal variations. The BSN and WSN flow model spectra differ mainly in their high SH degrees. As expected the BSN has less power than WSN there, whereas, for SH degrees around 4, it is the power spectrum of the WSN model that is the lowest. Although the WSN and BSN flow models are different, the SV corresponding to these models are nearly the same. Indeed one could impose constraints in order to build a flow model with specific and more realistic properties (e.g. tangential geostrophy, pure toroidal flow) leading to similar SV models, but that is not our goal here. The two flows obtained here have similar statistics: The BSN (resp. WSN) has a Kinetic Energy (KE) of 175.13 (km/yr)2 (resp. 128.26 (km/yr)2). Its toroidal component represent 82.88% (resp. 84.25%) of the KE and the geostrophic component represents 78.55% (resp. 77.58%) of the KE.
The BSN flow model is plotted in Fig. 9. The toroidal flow that dominates the general flow is remarkably smooth, but sufficiently complex to advect a core field model leading to a realistic SV model. Some attempts have been made to minimize further the poloidal component of the flow, but, these led to a degraded fit to the data set. The visual aspect of the WSN flow is similar to that of the BSN flow.
6. Conclusions
We derived a core magnetic field model spanning the 2004.87–2005.94 period from CHAMP satellite and observatory data. The field model is co-estimated together with a model of the flow at the top of the core and we impose the constraint that the field model closely follows the FF-hypothesis continuously in time. Despite the shortness of the data time span, the SV model is surprisingly accurate around 2005.4. Similarly the SA model can be resolved for the first SH degrees. However, our main point in this work has been to investigate how well a core field model inversion process can be regularized by constraints applied on the co-estimated flow model. In this respect, the results are very encouraging. First, we have shown that imposing a convergent spectrum on the flow immediately constrains the secular variation such that it can be downward continued without further regularization to the CMB. Second, we have shown that smoothing temporal variations of the flow affects the magnetic field acceleration magnitude.
In addition, we have seen that at the Earth’s surface the observed SA is mainly controlled by the temporal flow variations. We suggest that the background SA, that does not depend directly on the flow variations, defines a lower limit of the acceleration power spectrum for the core field compatible with the FF-hypothesis. Then, if the spectrum of a core magnetic field model acceleration falls below this limit, the time behavior of this field model is inconsistent with the FF-hypothesis. Deriving flow time variation information from such an anomalous model would be unlikely to lead to acceptable results. It would be interesting to test these hypotheses in a dynamo simulation where the induction equation is solved in a self-consistent manner.
In the approach used, the core flow model is truncated at relatively small SH degrees and, even if the flow has a rapidly converging spectrum, the interactions between the small scales of the field and the flow could be better accounted for. However, it is not straightforward in the presented framework. This will have to be investigated in a forthcoming study.
Diffusion necessarily exists and one could argue that imposing the FF-hypothesis constraint is not a valid approach at these timescales. We think nevertheless, that to impose the constraint is definitively an approach worth studying. Further, we observe that even under the flow constraints presented above, the error in Eq. (15) stays very small. Therefore, it is fairly easy to build a model respecting the FF-hypothesis, although that is not a sufficient condition to make the hypothesis valid. Some preliminary work has been done to apply the technique on data sets covering longer time span. There are no apparent serious further difficulties. However, this has to be investigated in detail in future work.
References
Asari, S., H. Shimizu, and H. Utada, Robust and less robust features in the tangential geostrophy core flows, Geophys. J. Int., 178(2), 678–692, 2009.
Beggan, C. D. and K. A. Whaler, Forecasting change of the magnetic field using core surface flows and ensemble kalman filtering, Geophys. Res. Lett., 36(18), 2009.
Bloxham, J., The determination of fluid flow at the core surface from geomagnetic observations, in Mathematical Geophysics, A Survey of Recent Developments in Seismology and Geodynamics, edited by Vlaar, N. J., Nolet, G., Wortel, M. J. R., and Cloetingh, S. A. P. L., 189–208, Reidel, Dordrecht, 1988.
Bloxham, J. and D. Gubbins, Geomagnetic field analysis. IV—Testing the frozen-flux hypothesis, Geophys. J. R. Astron. Soc., 84, 139–152, 1986.
Eymin, C. and G. Hulot, On core surface flows inferred from satellite magnetic data, Phys. Earth Planet. Inter., 152(3), 200–220, 2005.
Farquharson, C. and D. Oldenburgh, Non-linear inversion using general measures of data misfit and model structure, Geophys. J. Int., 134, 213–227, 1998.
Fournier, A., C. Eymin, and T. Alboussiére, A case for variational geomagnetic data assimilation: Insights from a one-dimensional, non-linear, and sparsely observed MHD system, Nonlin. Process. Geophys., 14(3), 163180, 2007.
Gillet, N., M. Pais, and D. Jault, Ensemble inversion of time-dependent core flow models, Geochem. Geophys. Geosyst., 10, Q06004, 2009.
Holme, R., Large-scale flow in the core, in Treatise on Geophysics, edited by Olson, P., volume 8, Elsevier Ltd., Amsterdam, 2007.
Jackson, A., Time-dependency of tangentially geostrophic core surface motions, Phys. Earth Planet. Inter., 103, 293–311, 1997. 516
Jackson, A., A. R. T. Jonkers, and M. R. Walker, Four centuries of geomagnetic secular variation from historical records, Phil. Trans. R. Soc. Lond. A, 358, 957–990, 2000.
Jackson, A., C. Constable, M. Walker, and R. Parker, Models of the Earth’s main magnetic field incorporating flux and radial vorticity constraints, Geophys. J. Int., 171(1), 133–144, doi:10.1111/j.1365-246X.2007.03526.x, 2007.
Jault, D. and J. L. Le Mouël, Physical properties at the top of the core and core surface motions, Phys. Earth Planet. Inter., 68,76–84, 1991.
Korte, M. and C. G. Constable, Continuous geomagnetic field models for the past 7 millennia II: CALS7K, Geochem. Geophys. Geosyst., 6, Q02H16, 2004.
Lesur, V., S. Macmillan, and A. Thomson, The BGS magnetic field candidate models for the 10th generation IGRF, Earth Planets Space, 57, 1157–1163, 2005.
Lesur, V., I. Wardinski, M. Rother, and M. Mandea, GRIMM—The GFZ Reference Internal Magnetic Model based on vector satellite and observatory data, Geophys. J. Int., 173, 2008.
Liu, D., A. Tangborn, and W. Kuang, Observing system simulation experiments in geomagnetic data assimilation, J. Geophys. Res., 112, B08103, doi:10.1029/2006JB004691, 2007.
Maus, S., S. McLean, D. Dater, H. Lühr, M. Rother, W. Mai, and S. Choi, NGDC/GFZ candidate models for the 10th generation International Geomagnetic Reference Field, Earth Planets Space, 57, 1151–1156, 2005.
Moon, W., Numerical evaluation of geomagnetic dynamo integrales, Com-put. Phys. Commun, 16, 267–271, 1979.
Olsen, N., A model of the geomagnetic field and its secular variationfor epoch 2000 estimated from Ørsted data, Geophys. J. Int., 149, 454–462, 2002.
Olsen, N. and M. Mandea, Rapidly changing flows in the Earth’s core, Nature Geosci., 1(6), 390–394, 2008.
Olsen, N., T. Sabaka, and F. Lowes, New parameterisation of external and induced fields in geomagnetic field modelling, and a candidate model for IGRF 2005, Earth Planets Space, 57, 1141–1149, 2005.
Olsen, N., H. Lühr, T. Sabaka, M. Mandea, M. Rother, L. Töffner-Clausen, and S. Choi, CHAOS—A model of the Earth’s magnetic field derived from CHAMP, Oersted, and SAC-C magnetic satellite data, Geophys. J. Int., 166(1), 67–75, 2006.
Rau, S., U. Christensen, A. Jackson, and J. Wicht, Core flow inversions tested with numerical dynamo models, Geophys. J. Int., 141, 485–497, 2000.
Roberts, P. H. and S. Scott, On the analysis of secular variation, 1, A hydromagnetic constraint: Theory, J. Geomag. Geoelectr, 17, 137–151, 1965.
Sabaka, T. J., N. Olsen, and M. E. Purucker, Extending comprehensive models of the Earth’s magnetic field with Ørsted and CHAMP data, Geophys. J. Int., 159, 521–547, 2004.
Thomson, A. and V. Lesur, An improved geomagnetic data selection algorithm for global geomagnetic field modelling, Geophys. J. Int., 169, 951–963, doi:10.1111/j.1365-246X.2007.03354.x, 2007.
Voorhies, C. V. and G. E. Backus, Steady flows at the top of the core from geomagnetic-field models— the steady motions theorem, Geophys. Astrophys. Fluid Dyn, 32, 163–173, 1985.
Waddington, R., D. Gubbins, and N. Barber, Geomagnetic-field analysis.5. Determining steady core-surface flows directly from geomagnetic observations, Geophys. J. Int., 122, 326–350, 1995.
Wardinski, I., R. Holme, S. Asari, and M. Mandea, The 2003 geomagnetic jerk and its relation to the core surface flows, Earth Planet. Sci. Lett., 267, 468–481, 2008.
Whaler, K. A., Geomagnetic evidence for fluid upwelling at the core-mantle boundary, Geophys. J. R. Astron. Soc., 86, 563–588, 1986.
Whaler, K. A. and R. Holme, Consistency between the flow at the top of the core and the frozen-flux approximation, Earth Planets Space, 59, 1219–1229, 2007.
Acknowledgements
We would like to acknowledge the work of CHAMP satellite processing team and of the scientists working in magnetic observatories. We would like also to thanks the reviewers for their constructive comments that certainly help in improving this manuscript. I. W. was supported by the European comission under contract No. 026670 (EC research project MAGFLOTOM). IPGP contribution 2611.
Author information
Authors and Affiliations
Corresponding author
Appendix A. The Field-Flow Time Parametrisation Inconsistency
Appendix A. The Field-Flow Time Parametrisation Inconsistency
In this appendix it is shown that the system of Eq. (15), derived from the diffusion-less induction equation does not have an exact solution if the basis functions ψ(t) are algebraic polynomials in time. Indeed, we know that there is no exact solution to Eq. (15) because the exclusion rules of the Gaunt and Elsasser integrals are such that the linear system is overdetermined; a solution can be obtained only by least squares. In practice, this solution is non-unique because some of the equations are severely under-weighted (sometimes simply ignored) as the SV is unknown at high SH degrees. However, we want to make clear that also in time, using truncated algebraic polynomial series as basis functions leads to solutions that can be only approximations of the exact solution. Rather than using Eq. (15), we start from the system (16) and re-write in a more general case:

where the function P(t) corresponds to the magnetic field coefficients and the series  stands for the A
u
(t) matrix that we expand as an algebraic polynomial in time in order to describe the flow time variations. The full proof for the general case is outside the scope of this manuscript*1. We rather address here the simple case where only a dependence in tj−1 is considered.
stands for the A
u
(t) matrix that we expand as an algebraic polynomial in time in order to describe the flow time variations. The full proof for the general case is outside the scope of this manuscript*1. We rather address here the simple case where only a dependence in tj−1 is considered.
We look for polynomial solutions of the following equation

where Qj−1 is a n × n dimensional matrix. If λ and η are an eigenvalue and the corresponding eigenvector of the matrix Qj−1, then the vector:

satisfies the Eq. (A.2). If all real or complex eigenvalues of Qj−1 are distinct (with multiplicity 1), then the fundamental solution of (A.2) is a linear combination of vectors of the form (A.3). In order to obtain a polynomial solution of Eq. (A.2), we must consider the case where λ = 0 is the only eigenvalue of Qj− 1 and therefore has multiplicity n.
If is an eigenvalue of Qj−1 with multiplicity n,weneed to find n linearly independent solutions of (A.2). In this case the following result holds.
Theorem 1If λ is an eigenvalue ofQj − 1with multiplicity n, then every solution P(t) of Eq. (A.2) has the form

where

It is easy to check by direct substitution that the vectors  satisfy Eq. (A.2). They are also linearly independent and therefore form a fundamental set of solutions.
satisfy Eq. (A.2). They are also linearly independent and therefore form a fundamental set of solutions.
Since we are interested in polynomial solutions of Eq. (A.2), it is clear that they can be obtained only if λ = 0. Having all eigenvalues equal to zero is a very restrictive requirement that is not relevant for the problem we are considering here. We therefore conclude that an algebraic polynomial expansion for the time representation should not be used for both the magnetic field and flow models in order to obtain exact solutions to the system of Eq. (15).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lesur, V., Wardinski, I., Asari, S. et al. Modelling the Earth’s core magnetic field under flow constraints. Earth Planet Sp 62, 503–516 (2010). https://doi.org/10.5047/eps.2010.02.010
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.5047/eps.2010.02.010

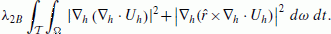
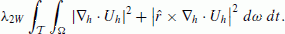

 denotes the flow time derivative. We expect such a constraint to efficiently regularize the inverse problem as in the limit of a constant flow there is a unique flow solution of the FF-equation (Voorhies and Backus,
denotes the flow time derivative. We expect such a constraint to efficiently regularize the inverse problem as in the limit of a constant flow there is a unique flow solution of the FF-equation (Voorhies and Backus, 







