Comparative Studies of the Plasma at Non-magnetized Planets/Moons
- Article
- Open access
- Published:
Effect of ion cyclotron motion on the structure of wakes: A Vlasov simulation
Earth, Planets and Space volume 64, pages 231–236 (2012)
Abstract
The global structure of wake fields behind an unmagnetized object in the solar wind is studied by means of a 2.5-dimensional full electromagnetic Vlasov simulation. The interaction of a plasma flow with an unmagnetized object is quite different from that with a magnetized object such as the Earth. Due to the absence of the global magnetic field, the unmagnetized object absorbs plasma particles which reach the surface, generating a plasma cavity called a wake on the anti-solar side of the object. The interaction between the solar wind with an out-of-plane interplanetary magnetic field and an unmagnetized object of ion-gyro scale is examined to study the effect of the ion cyclotron motion on the structure of wake fields. It is shown that the wake boundary layer is broadened when the inner product of the electric force and the density gradient of the wake boundary layer is negative. On the other hand, a steep wake boundary layer is formed with a negative inner product. The result suggests that the structures of wake fields become asymmetric due to the in-plane E cross B drift motion of ions.
1. Introduction
Computer simulations are now essential approaches for studies of space plasma, since space plasma is a collisionless, multi-scale, and highly nonlinear medium. There are numerous types of self-consistent computer simulations that treat plasma according to some approximation. The macroscopic (global-scale) dynamics in space plasma are commonly described by magneto-hydro-dynamic (MHD), Hall-MHD and multi-fluid models, while microscopic (electron-scale) processes are described by the full-kinetic models, i.e., the Maxwell equations and either the Newton-Lorentz equation for charged particles or the Vlasov (collisionless Boltzmann) equation. Hybrid methods treat ions as particles and electrons as a fluid for mesoscopic (ion-scale) processes.
Conventionally, MHD simulations have been used for studies of macroscopic phenomena. However, MHD simulations need resistivity, conductivity, adiabatic index, and diffusion coefficients. These quantities are essentially due to first-principle kinetic processes that are eliminated in the framework of the MHD approximation. Recent highresolution in-situ observations have also suggested that macroscopic, mesoscopic and microscopic processes in space plasma are strongly coupled with each other, which is called cross-scale coupling. To understand the cross-scale coupling in space plasma, it is important to include full kinetics of plasma particles in global- and macro-scale simulations. However, this requires enormous computing resources.
The interaction between the solar/stellar wind and geo-physical/astrophysical objects, such as planets, satellites and asteroids, is one of the fundamental global-scale problems in space plasma. In the present study, we especially focus on an unmagnetized object in the solar wind. Due to the absence of the global magnetic field, plasma particles can reach the surface of the object. There appears a plasma cavity called the “wake” on the anti-solar side of the object by the absorption of plasma particles at the surface of the object.
Electromagnetic structures of the wake have been studied by hybrid PIC simulations (Kallio, 2005; Travnicek et al., 2005) and by full PIC simulations (Birch and Chapman, 2001, 2002; Guio and Pecseli, 2004, 2005; Kimura and Nakagawa, 2008). In the previous full PIC simulations (Birch and Chapman, 2001; Guio and Pecseli, 2004, 2005; Kimura and Nakagawa, 2008) particle entry into the plasma void due to thermal diffusion was considered, but the effect of the ion cyclotron motion was not included. Since the thermal cyclotron radius of ions is large, ion cyclotron motion may play an essential role for the entry of ions into the wake (e.g., Nishino et al., 2009).
In general, the radius of the object is set to be 10–100 times as large as the thermal cyclotron radius of ions in hybrid PIC simulations. On the other hand, the radius of the object is set to be 10–100 times as large as the Debye length in full PIC simulations. This means that the radius of the object is about 10 times as large as the thermal cyclotron radius of electrons. These are due to a numerical constraint that the grid spacing Δ must be as short as the Debye length. One can also include the effect of the ion cyclotron motion when the ion-to-electron mass ratio is reduced (e.g., Birch and Chapman, 2002) or the external magnetic field is enlarged (Nakagawa and Kimura, 2011). It has also been shown that the magnitude of the wake field can be enhanced by a charging of the surface of the object (Kimura and Nakagawa, 2008). The charging effect cannot be included in the hybrid method but can in the full kinetic method.
The Vlasov method, which follows the spatial and temporal developments of distribution functions defined in the position-velocity phase space, is considered to be an alternative to the PIC method. The Vlasov method is free from any numerical noise, and allows us to relax the constraint of grid spacing. That is, one can set the grid spacing Δ to be much longer than the electron Debye length (e.g., Umeda et al., 2009). On the other hand, one needs a huge number of grid points in both the configuration, and velocity, spaces to treat the six-dimensional phase space, which is a big drawback of the current Vlasov model. However, numerical techniques for the Vlasov model are rapidly developing, and the recent development of hardware technology also allows us to perform hyper-dimensional Vlasov simulations. Thus, the Vlasov method might be an appropriate approach for including both the charging effect and the ion cyclotron motion.
Very recently, Umeda et al. (2011) succeeded in carrying out a two-and-half-dimensional (2.5D) Vlasov simulation of the interaction between the solar wind and a small dielectric object. They studied the effect of the interplanetary magnetic field (IMF) on the structure of wake fields by applying an in-plane IMF to the two-dimensional (2D) configuration space, where the in-plane cyclotron motion was not solved. In the present study, therefore, we apply an out-of-plane IMF in order to include the in-plane cyclotron motion. It should be noted that we do not include the scattering of ions on the dayside lunar surface by a magnetic anomaly (e.g., Nishino et al., 2009), and that the thermal cyclotron motion of ions is considered.
This paper is structured as follows. In Section 2, numerical techniques for the full electromagnetic Vlasov code are briefly reviewed. In Section 3, a simulation setup for the interaction of the solar wind with an unmagnetized body is described. In Section 4, numerical results are presented. The summary is given in Section 5.
2. Brief Review of Vlasov Code
The Vlasov model solves the full-set of the Maxwell equations (1) and the Vlasov equation (2),


where E, B, J, ρ, μ0, ϵ0 and c represent electric field, magnetic field, current density, charge density, magnetic permeability, dielectric constant and light speed, respectively. The distribution functions fs (r, v, t) are defined in position-velocity phase space. The subscript s represents the singly-charged ions and electrons (e.g., s = i, e), although the code allows arbitrary species. The quantities q s and m s are the charge and mass of particle species s. The current density J is determined so that ρ and J satisfy the current-continuity equation

The Vlasov equation (2) consists of two advection equations with a constant advection velocity and a rotation equation by a centripetal force without diffusion terms. To simplify the numerical time-integration of the Vlasov equation, we adopt an operator splitting technique (e.g., Cheng and Knorr, 1976; Ghizzo et al., 2003). By using a modified version of the operator splitting, the Vlasov equation splits into the following three equations (Umeda et al., 2009),



Equations (4) and (5) are scalar (linear) advection equations in which v and E are independent of r and v, respectively.
We adopt a multi-dimensional conservative semi-Lagrangian scheme (Umeda et al., 2009) for solving the multidimensional advection equations. In the full electromagnetic method, it is essential to use conservative schemes for satisfying the continuity equation for charge. With the multi-dimensional conservative semi-Lagrangian scheme, the solution to the advection equation in the configuration space (4) is given by

where U = (U x , U y , U z ) represent numerical flux in the configuration space, and the subscript s is omitted. One can find that the above equation exactly satisfies the continuity equation for charge (3) with


It is noted that conservative schemes also have advantages in easiness for introducing slope limiters in the reconstruction to ensure specific properties such as positivity and monotonicity (e.g., Filbet et al., 2001; Umeda, 2008; Crouseilles et al., 2010). In the present study, we adopt a positive, non-oscillatory and conservative limiter (Umeda, 2008; Umeda et al., submitted) for stable time-integration of advection equations. Equation (6), on the other hand, is a multi-dimensional rotation equation which follows a circular motion of a profile at constant speed by a centripetal force. For stable rotation of the profile on the Cartesian grid system, the “back-substitution” technique (Schmitz and Grauer, 2006) is applied. In addition, the Maxwell equations are solved by the implicit Finite Difference Time Domain (FDTD) method (e.g., Hoshino, 1986) on the Yee grid system (Yee, 1966), which is free from the Courant condition for electromagnetic light mode waves.
The Maxwell-Vlasov system is advanced by using the following sequences (Umeda et al., 2009), which is consistent with the second-order leap-frog time-integration algorithm used in particle-in-cell simulations.
-
1)
Shift phase-space distribution functions in the configuration space with the full time step Δt by using the multi-dimensional conservative scheme (Umeda et al., 2009).
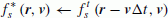 (10)
(10) -
2)
Compute the current density by integrating the numerical flux U over the velocity v as Eq. (9).
-
3)
Advance electromagnetic fields from t to t + Δt by solving the Maxwell equations with the implicit FDTD method.
-
4)
Shift phase-space distribution functions in the velocity space by an electric force with the half time step Δt/2 by using the multi-dimensional conservative scheme (Umeda et al., 2009).
 (11)
(11) -
5)
Rotate phase-space distribution functions in the velocity space by a magnetic force with the full time step Δt by using the back-substitution scheme (Schmitz and Grauer, 2006).
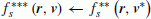 (12)
(12)where
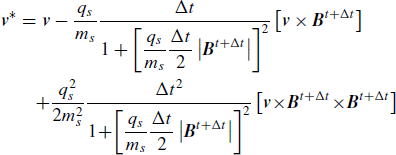
-
6)
Shift phase-space distribution functions in the velocity space by an electric force with the half time step Δt/2 by using the multi-dimensional conservative scheme (Umeda et al., 2009).
 (13)
(13)
The detailed descriptions of the numerical schemes are provided by Schmitz and Grauer (2006); Umeda (2008); Umeda et al. (2009).
In the present Vlasov code, there is a numerical constraint on the CFL condition for rotation in velocity space by magnetic fields. For stable rotation of distribution functions with the back-substitution scheme on the Cartesian grid system, we choose the timestep Δt such that

where B0 represents an ambient magnetic field. This means that the timestep Δt must be taken to be small for strongly magnetized plasma.
Note that the present Vlasov code has been successfully applied to magnetic reconnection (Umeda et al., 2009, 2010a), the Kelvin-Helmholtz instability (Umeda et al., 2010b) and the interaction between the solar wind and an unmagnetized dielectric body (Umeda et al., 2011). As demonstrated by these studies, a numerical constraint on the spatial grid can be relaxed in the full-electromagnetic Vlasov simulation. That is, the grid spacing can be taken to be much longer than the electron Debye length, if the Debye-scale physics can be negligible. It should be noted, however, that low resolutions in configuration, or velocity, spaces sometimes cause a numerical diffusion of physical structures.
3. Simulation Setup
We assume a 2.5D Cartesian system in which spatial grids are taken in the 2D x−y plane and velocity grids are taken in the 3D v x −v y −v z space. There exists an insulative sphere at (x, y) = (0, 0), in which the charge accumulates on the surface. The radius of the object is set to be R S = 100λ D where λ D is the Debye length. The system size of the simulation box is L x × L y = 4000λ D × 2000λ D (−10R S ≤ L x ≤ 30R S and −10R S ≤ L y ≤ 10R S ), and we use N x × N y = 400 × 200 grid points. Thus, the grid size is Δ = Δx = Δy = 10 λ D = 0.1R S . At all edges and corners of the simulation box, we applied so-called absorbing boundary conditions to suppress non-physical reflection of electromagnetic waves. For the velocity space, we use N vx × N vy × N vz = 40 × 40 × 40 grid points. The range of the velocity space is taken to be −20V ti ≤ v i ≤ 20V ti and − 10V te ≤ v e ≤ 10V te for all v x , v y and v z directions. We used about 160 GB of memory for the present 5D Vlasov simulation performed with 256 cores on massively-parallel scalar computer systems.
There exists a uniform plasma flow in the simulation box at the initial state. The plasma flow is directed in the x direction with a flow velocity V s = 12V ti , where V ti is the thermal velocity of ions. The uniform plasma flow is continuously injected from the left boundary, i.e., x = − 1000 λ D , to the right. In order to save computational costs, electrons are assumed to be much heavier than in reality with a mass ratio m i /m e = 100. Assuming that the ions and electrons have the same temperature (T i /T e = 1.0), the thermal velocity of electrons becomes V tr = 10V ti . We also reduce the light speed for computational efficiency as c/V ti = 200.
The solar wind carries an IMF, which is the intrinsic magnetic field of the Sun. In the present study, an ambient magnetic field, such as the IMF, is taken in the z (out-of-plane) direction. The magnitude of the ambient magnetic field is given by B z0 = m i /q i ω ci with ω ci /ω pi = 0.01, where ω c and ω p are the cyclotron and plasma angular frequency, respectively. Thus, the radius of the body and the grid spacing with respect to the gyro radius r are R S = r i = 10r e and Δ = 0. 1r i = r e , respectively. To carry the ambient magnetic field in the plasma flow direction, we need a uniform electromotive (Faraday’s inductive) force. A uniform external electric field is applied in the y direction with the magnitude of E y0 = V s B z0 .
There exists an inner boundary at x2 + y2 = R S . We assume that the electric conductivity of the object is small, like an insulator. Numerically, the spatial numerical flux in Eq. (7) is set to be zero for x2 + y2 < R S . Then, spatial advection in the object is not allowed and the electric charge of plasma particles onto the object accumulates on the surface of the object. Note that we do not use any special treatment for electromagnetic waves at the inner boundary. That is, electromagnetic waves propagate freely into the object without conductance.
Suppose a typical velocity of the solar wind and the thermal velocity of ions are V S = 400 km/s and V ti = 50 km/s (i.e., about 26 eV), respectively, and a typical ion density is N i = 10 cm−3, the ion plasma frequency and Debye length become about f pi = 664 Hz and λ Di = 75 m, respectively. Thus the radius of the object becomes about R S = 7.5 km, which corresponds to the typical size of an asteroid. The ion cyclotron frequency and the gyro radius become about f ci = 6.6 Hz and r i = 7.5 km, respectively.
4. Simulation Results
Figure 1 shows the spatial profiles of the ion density N i , the electric field ΔE y and ΔR x components (the external electric field E y0 subtracted) at ω ci t = 1.0. Here, we do not show the spatial profiles of the electron density, because the quasi-charge-neutrality is well satisfied in a spatial scale much larger than the Debye length. It should be noted, however, that the spatial charge separation between ions and electrons is resolved in a low-density wake region with N i , N e ≪ 0.3.
The plasma void is formed on the nightside of the body while plasma particles accumulate on the dayside surface of the body. Since the thermal velocity of ions is much smaller than the flow velocity, all the ions accumulate on the dayside of the body. On the other hand, since the thermal velocity of electrons is larger than the flow velocity, only forward-streaming electrons accumulate on the day-side of the body. Thus, the dayside of the body is positively charged. In contrast, the nightside region of the body is negatively charged since the thermal electrons can reach there. (Kimura and Nakagawa, 2008; Umeda et al., 2011).
On both sides of the plasma void in the nightside, there exist electric fields called “wake” fields. In regions very close to the body, a strong wake field is excited in the direction toward the body (Kimura and Nakagawa, 2008; Umeda et al., 2011). As the distance from the body becomes great, the structure of the upper (+y) side of the wake field becomes bipolar while the intensity of the wake field becomes smaller on the lower (−y) side. This asymmetric feature is different from the structure of the wake field seen in the previous Vlasov simulation (Umeda et al., 2011) where the IMF is taken in the in-plane directions (x–y plane). It is noted that there appear spatial oscillations on the noon-side of the object because of a numerical effect due to a lack of spatial resolution for a Debye sheath (Umeda et al., 2011).
In the present simulation with the out-of-plane IMF, the trajectory of the  drift motion of ions becomes a trochoid. In this case, one may understand that ions with a large gyro radius can penetrate into the wake from the upper (+y ) side of the wake, where the electric force
drift motion of ions becomes a trochoid. In this case, one may understand that ions with a large gyro radius can penetrate into the wake from the upper (+y ) side of the wake, where the electric force  and the density gradient ∇n are in the same direction, i.e.,
and the density gradient ∇n are in the same direction, i.e.,  On the other hand, ions with a large gyro radius are absorbed on the surface of the insulative body and cannot penetrate into the wake from the lower (−y) side of the wake where
On the other hand, ions with a large gyro radius are absorbed on the surface of the insulative body and cannot penetrate into the wake from the lower (−y) side of the wake where  . This feature might result in the asymmetric structure of the wake fields.
. This feature might result in the asymmetric structure of the wake fields.
Figure 2 shows the slices of the ion density N
i
, electric field ΔE
y
and ΔE
x
components. We found that there are more ions at y = 1 than at y = −1, which is consistent with the ion entry process into the wake described above. For x > 2, on the other hand, there are more ions at y = −0.5 than at y = 0.5. It is also found that the density gradient of the wake boundary layer becomes steeper on the positive  side of the wake than on the negative
side of the wake than on the negative  side. On the negative
side. On the negative  side of the wake, the electric field E
y
component has a positive unipolar signature by which the plasma convection is directed in the +x direction. On the positive
side of the wake, the electric field E
y
component has a positive unipolar signature by which the plasma convection is directed in the +x direction. On the positive  side of the wake, by contrast, the electric field E
y
component has a bipolar signature which maintains the steep wake boundary layer. There also exists a strong electric field E
x
component around the body due to the surface charging (Kimura and Nakagawa, 2008). The plasma convection is directed in the +y direction by the negative E
x
component which results in the entry of ions from the negative
side of the wake, by contrast, the electric field E
y
component has a bipolar signature which maintains the steep wake boundary layer. There also exists a strong electric field E
x
component around the body due to the surface charging (Kimura and Nakagawa, 2008). The plasma convection is directed in the +y direction by the negative E
x
component which results in the entry of ions from the negative  side of the wake.
side of the wake.
Let us analyze the electromagnetic structures of the wake field (ΔE y ) by using the generalized Ohm’s law.

The steady-state solution to the generalized Ohm’s law becomes

We found that the second term (−U
ze
B
x
), the off-diagonal pressure-gradient term  , and the advection terms in the second line of Eq. (15) are very small. In Fig. 3, we show the spatial profiles of the electron pressure-gradient term
, and the advection terms in the second line of Eq. (15) are very small. In Fig. 3, we show the spatial profiles of the electron pressure-gradient term  and the electron convection term (−U
ze
B
x
) at ω
ci
t=1.0.
and the electron convection term (−U
ze
B
x
) at ω
ci
t=1.0.
The electron pressure-gradient term is negative in a narrow region on the upper (+y) side of the void, while this term is strongly positive near the body but is small at distant regions from the body on the lower (−y) side. This feature suggests an anisotropic structure of the electron/ion density. The electron convection term has an opposite polarity to the electron pressure-gradient term on the upper (+y) side, while this term is strongly negative at the center of the void. The electron convection term cancels the electron pressure-gradient term, generating the bipolar structure of E y on the upper (+y ) side.
It should be noted that it is difficult to discuss the origin of the wake electric field in terms of the steady-state equation of motion for an ion fluid,

First, all the terms except for the ion convection term (−U zi B x ) are dominant. Second, this equation is invalid around the center of the wake because the effect of the charge separation is excluded.
The pressure-gradient terms and the ion advection terms are strongly enhanced near the body, but they weaken each other. The diagonal pressure-gradient term  and the ion convection term (U
xi
B
z
) show an asymmetric feature, while the ion advection term
and the ion convection term (U
xi
B
z
) show an asymmetric feature, while the ion advection term  shows a sym-metric feature. Although the off-diagonal pressure-gradient term
shows a sym-metric feature. Although the off-diagonal pressure-gradient term  is asymmetric, this term is smaller than other terms.
is asymmetric, this term is smaller than other terms.
5. Summary
By using a 5D (2D configuration, and 3D velocity, spaces) full-electromagnetic Vlasov simulation, we studied the interaction between the solar wind with an out-of-plane IMF and an unmagnetized object of ion-gyro scale. Since the spatial size of the astrophysical object is set to be equal to the ion gyro radius, the effect of a finite ion gyro radius is of interest. Since the IMF is taken in the out-of-plane (z) direction in order to solve the in-plane (x−y plane) gyro motion, the trajectory of the  drift motion becomes a trochoid. Test particle ions with a large gyro radius can penetrate into the wake in the case of positive
drift motion becomes a trochoid. Test particle ions with a large gyro radius can penetrate into the wake in the case of positive  but not in the case of negative
but not in the case of negative  The present self-consistent Vlasov simulation result has shown that the entry process of thermal ions into the wake is different from the prediction described above.
The present self-consistent Vlasov simulation result has shown that the entry process of thermal ions into the wake is different from the prediction described above.
The density gradient of the wake boundary layer becomes steeper with positive  while the wake boundary layer is broadened with negative
while the wake boundary layer is broadened with negative  . There appears a strong bipolar electric field due to the Hall effect with positive
. There appears a strong bipolar electric field due to the Hall effect with positive  , which maintains the steep wake boundary layer. The ion entry from the negative
, which maintains the steep wake boundary layer. The ion entry from the negative  side is due to the plasma convection (−E
x
× B
z
motion). Note that these features are different from the structure of the wake field obtained in the previous Vlasov simulation where the IMF is taken in the in-plane direction (x−y plane). The trajectory of the
side is due to the plasma convection (−E
x
× B
z
motion). Note that these features are different from the structure of the wake field obtained in the previous Vlasov simulation where the IMF is taken in the in-plane direction (x−y plane). The trajectory of the  drift motion becomes a sinusoid with the in-plane IMF, and the structure of the wake field becomes symmetric.
drift motion becomes a sinusoid with the in-plane IMF, and the structure of the wake field becomes symmetric.
The present and previous Vlasov simulation results suggest that structures of wakes are determined by the ion convection, and a 6D simulation (with three spatial dimensions) is essential for a full understanding of the electromagnetic structures of wakes. However, this requires a Peta-scale computer, and is left as a future study.
References
Birch, P. C. and S. C. Chapman, Particle-in-cell simulations of the lunar wake with high phase resolution, Geophys. Res. Lett., 28, 219–222, 2001.
Birch, P. C. and S. C. Chapman, Two dimensional particle-in-cell simulations of the lunar wake, Phys. Plasmas, 9, 1785–1789, 2002.
Cheng, C. Z. and G. Knorr, The integration of the Vlasov equation in configuration space, J. Comput. Phys., 22, 330–351, 1976.
Crouseilles, N., M. Mehrenberger, and E. Sonnendrucker, Conservative semi-Lagrangian schemes for Vlasov equations, J. Comput. Phys., 229, 1927–1953, 2010.
Filbet, F., E. Sonnendrucker, and P. Bertrand, Conservative numerical schemes for the Vlasov equation, J. Comput. Phys., 172, 166–187, 2001.
Ghizzo, A., F. Huot, and P. Bertrand, A non-periodic 2D semi-Lagrangian Vlasov code for laser-plasma interaction on parallel computer, J. Com-put. Phys., 186, 47–69, 2003.
Guio, P. and H. L. Pecseli, Phase space structures generated by an absorbing obstacle in a streaming plasma, Geophys. Res. Lett., 31, L03806, 2004.
Guio, P. and H. L. Pecseli, Phase space structures generated by absorbing obstacles in streaming plasmas, Ann. Geophys., 23, 853–865, 2005.
Hoshino, M., Theoretical and computational studies of plasma kinetic phenomena: Tearing mode instability and foreshock cyclotron interaction, Ph.D. thesis, University of Tokyo, 1986.
Kallio, E., Formation of the lunar wake in quasi-neutral hybrid model, Geophys. Res. Lett., 32, L06107, 2005.
Kimura, S. and T. Nakagawa, Electromagnetic full particle simulation of the electric field structure around the moon and the lunar wake, Earth Planets Space, 60, 591–599, 2008.
Nakagawa, T. and S. Kimura, Role of the solar wind magnetic field in the interaction of a non-magnetized body with the solar wind: An electromagnetic 2-D particle-in-cell simulation, Earth Planets Space, 63, 477–486, 2011.
Nishino, M., M. Fujimoto, K. Maezawa, Y. Saito, S. Yokota, K. Asamura, T. Tanaka, H. Tsunakawa, M. Matsushima, F. Takahashi, T. Terasawa, H. Shibuya, and H. Shimizu, Solar-wind proton access deep into the near-Moon wake, Geophys. Res. Lett., 36, L16103, 2009.
Schmitz, H. and R. Grauer, Comparison of time splitting and backsubstitution methods for integrating Vlasov’s equation with magnetic fields, Comput. Phys. Commun., 175, 86–92, 2006.
Travnicek, P., P. Hellinger, D. Schriver, and S. D. Bale, Structure of the lunar wake: Two-dimensional global hybrid simulations, Geophys. Res. Lett., 32, L06102, 2005.
Umeda, T., A conservative and non-oscillatory scheme for Vlasov code simulations, Earth Planets Space, 60, 773–779, 2008.
Umeda, T., K. Togano, and T. Ogino, Two-dimensional full-electromagnetic Vlasov code with conservative scheme and its application to magnetic reconnection, Comput. Phys. Commun., 180, 365–374, 2009.
Umeda, T., K. Togano, and T. Ogino, Structures of diffusion regions in collisionless magnetic reconnection, Phys. Plasmas, 17, 052103, 2010a.
Umeda, T., J. Miwa, Y. Matsumoto, T. K. M. Nakamura, K. Togano, F. Fukazawa, and I. Shinohara, Full electromagnetic Vlasov code simulation of the Kelvin-Helmholtz instability, Phys. Plasmas, 17, 052311, 2010b.
Umeda, T., T. Kimura, K. Togano, K. Fukazawa, Y. Matsumoto, T. Miyoshi, N. Terada, T. K. M. Nakamura, and T. Ogino, Vlasov simulation of the interaction between the solar wind and a dielectric body, Phys. Plasmas, 18, 012908, 2011.
Yee, K. S., Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media, IEEE Trans. Antenn. Prop-agat., AP-14, 302–307, 1966.
Acknowledgments
The author thanks Yosuke Ito for discussions. This work was supported by MEXT/JSPS under Grant-in-Aid for Young Scientists (B) No. 21740352 and No. 23740367. The computer simulations were performed on the Fujitsu FX1 and HX600 supercomputer systems at the Information Technology Center, Nagoya University, and the Hitachi HA8000 (T2K) supercomputer system at the Information Technology Center, the University of Tokyo. The computational resources were provided by the Solar-Terrestrial Environment Laboratory and the Information Technology Center, Nagoya University, as HPC joint research programs and by the Joint Usage/Research Center for Interdisciplinary Large-Scale Information Infrastructures as a JHPCN program (PI: T. Ogino).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Umeda, T. Effect of ion cyclotron motion on the structure of wakes: A Vlasov simulation. Earth Planet Sp 64, 231–236 (2012). https://doi.org/10.5047/eps.2011.05.035
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.5047/eps.2011.05.035
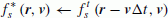

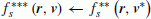
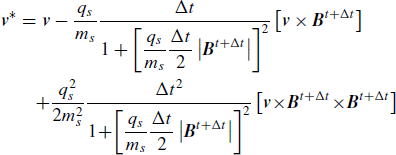




 and U
xe
B
x
at ω
ci
t = 1.0. The electric field is normalized by ǀB
0
V
S
ǀ. The distance is normalized by the radius of the object R
S
.
and U
xe
B
x
at ω
ci
t = 1.0. The electric field is normalized by ǀB
0
V
S
ǀ. The distance is normalized by the radius of the object R
S
.