Comparative Studies of the Plasma at Non-magnetized Planets/Moons
- Article
- Open access
- Published:
Hybrid simulations of proton precipitation patterns onto the upper atmosphere of Mars
Earth, Planets and Space volume 64, pages 121–134 (2012)
Abstract
We study the dependence of proton precipitation patterns onto the Martian upper atmosphere on altitude, proton energy, proton origin, and in a lesser extent, solar zenith angle, using the HYB-Mars model, a 3D quasineutral hybrid model. We find that the flux of precipitating protons has a strong altitude dependence: on the dayside, the flux of precipitating protons decreases substantially when the altitude over Mars decreases. We also find that the contribution of exospheric protons to the deposition is significant and its spatial distribution is not identical to that of the solar wind protons. In addition, the low energy proton population comes mainly from the newborn planetary protons. The energized pick-up protons and solar wind protons contribute to the higher energy proton population. The study also confirms that the proton precipitation is highly asymmetric with respect to the direction of the convection electric field in the solar wind. The study implies that the Martian induced magnetosphere protects the upper atmosphere effectively against proton precipitation.
1. Introduction
The interaction of the supersonic solar wind with an un-magnetized planet like Mars leads to the formation of an induced magnetosphere: the flow is decelerated and diverted around the conductive ionosphere due to the magnetic field associated with the induced currents, and the interplanetary magnetic field (IMF) frozen into the flow drapes around the obstacle, forming a magnetic barrier on the dayside and a magnetotail on the nightside (e.g. Nagy et al., 2004). The induced magnetospheric boundary separates the magnetosheath, dominated by solar wind protons, from the ionosphere, dominated by heavy ions . However, the gyroradius of some solar wind protons may be large enough due to their high energy, so that they can penetrate the magnetic barrier and reach the upper atmosphere, carrying energy, matter and momentum.
. However, the gyroradius of some solar wind protons may be large enough due to their high energy, so that they can penetrate the magnetic barrier and reach the upper atmosphere, carrying energy, matter and momentum.
The solar wind proton precipitation on Mars has been studied with hybrid models (Brecht, 1997; Kallio and Janhunen, 2001). Since the hybrid models treat the protons as individual gyrating particles, they are well suited to study proton precipitation. Brecht (1997) has shown that the precipitation is sensitive to upstream solar wind conditions, that is, the solar wind bulk velocity , and the direction of the interplanetary magnetic field
, and the direction of the interplanetary magnetic field . Results from Brecht (1997) and Kallio and Janhunen (2001) also show an asymmetry in the proton precipitation associated with the direction of the solar wind convection electric field
. Results from Brecht (1997) and Kallio and Janhunen (2001) also show an asymmetry in the proton precipitation associated with the direction of the solar wind convection electric field . More H+ ions are deposited on the hemisphere where the electric field points away from the planet (
. More H+ ions are deposited on the hemisphere where the electric field points away from the planet ( hemisphere) than on the opposite hemisphere (
hemisphere) than on the opposite hemisphere ( hemisphere).
hemisphere).
The purpose of the present paper is to study the proton precipitation on Mars and its dependence on altitude, energy and origin of the particles, using the HYB-Mars model (Kallio et al., 2010, and references therein), a 3D quasi-neutral hybrid model. Although proton precipitation has already been modeled with hybrid simulations, this is the first study which examines the spatial precipitation patterns given by the solar wind protons and the protons of planetary origin, at different altitudes, for different energy ranges of precipitating protons.
The current paper is an attempt to better understand measurements of downgoing proton flux in the Martian ionosphere made by Mars Express. Observations of solar wind protons in the Martian ionosphere down to 260 km altitude (the pericenter of the orbit of Mars Express, slightly above the exobase) have been reported by Lundin et al. (2004). A case study by Diéval et al. (submitted, 2011) compared Mars Express observations of downgoing proton flux in the ionosphere to simulated proton energy spectra derived from a hybrid simulation, in a similar way as was done by Kallio et al. (2008). The current study is a further step. We want to get a global view of the proton precipitation, using nominal solar wind conditions, to guide the interpretation of future observational statistical studies of proton precipitation onto the Martian atmosphere.
In the present study we keep the solar wind conditions and the solar activity constant: we use an average solar wind speed and minimum solar activity. This choice is motivated by the fact that the operation period of Mars Express (since 2004) coincides with low solar activity. The effect of the oxygen corona on the proton precipitation, the proton backscattering and the energetic neutral atoms production are beyond the scope of this study.
The basic characteristics of the model and the needed inputs are described in Section 2. The results are presented in Section 3 and discussed in Section 4.
2. Model
The HYB-Mars model is described in detail in the paper by Kallio et al. (2010) and references therein. Here we do not explain the details of the code but repeat the basics and describe what is new compared to the work by Kallio et al. (2010). HYB-Mars is a Particle-in-Cloud (PIC) model where an ion is a cloud (macroparticle), which has the same size as the cell, in which the center of cloud is located (see Kallio and Janhunen, 2003, for details). The macroparticle corresponds to w real particles. The weight w depends on the ion specie and its value is typically 1020−1022.
In the model, the plasma ions are treated as particles and the electrons are treated as a massless charge-neutralizing fluid. The ions are accelerated by the Lorentz force:

where and
and are the electromagnetic fields, m
i
the mass of an ion
are the electromagnetic fields, m
i
the mass of an ion the velocity of an ion i and q
i
the electric charge of an ion i. The electric field is calculated from the electron momentum equation:
the velocity of an ion i and q
i
the electric charge of an ion i. The electric field is calculated from the electron momentum equation:

where n
e
is the electron density, T
e
the electron temperature, the electron bulk velocity, e the unit electron charge and k Boltzmann’s constant. The last term in Eq. (2) is the electron gradient pressure, also referred to the ambipolar electric field.
the electron bulk velocity, e the unit electron charge and k Boltzmann’s constant. The last term in Eq. (2) is the electron gradient pressure, also referred to the ambipolar electric field.
The coordinate system used is the Mars Solar Orbital (MSO) Cartesian coordinate system. The x-axis points from the center of Mars towards the Sun, the z-axis points towards the orbital North and the y-axis completes the right-handed system. The size of the simulation box is −4.2 Rm < x, y, z < 4.2 R m , where R m = 3393 km is the Martian radius. The simulation uses three different grid sizes, depending on the distance r from the center of Mars: 720 km for r > 3 Rm, 360 km for 2 Rm < r < 3 Rm and 180 km for r < 2 Rm. The time step is 0.02 s, and the average number of particles per grid cell is ~30, which is significant. The total running time was ~700 s.
It is noteworthy that the crustal magnetic anomalies (Acuña et al., 1998, 1999) are not included into the model because the grid size is too coarse to model the intrinsic magnetic field accurately. The magnetic field is saved on the face of the cells and even the smallest grid size (180 km) would be too large to model the crustal magnetic anomalies accurately enough. The large grid size may, therefore, reduce the gradients of the electric and magnetic fields of the model and can result in a smoothed electromagnetic field. Ions within the grid cell are, however, subject to gyromo-tion caused by the Lorentz force (Eq. (1)) within a grid cell, also in the situation where the grid size is larger than the ion gyroradius. In general, the smallest grid size in the simulation, 180 km, is still relative large compared with the interaction region. How the grid size affects the solution is an issue which should be studied in the future with hybrid model simulations with a finer grid size than in the present study.
We believe that the crustal magnetic anomalies may inhibit the downward proton flux to the atmosphere, at least in regions where the field is not radial. We base this hypothesis on the work of Shematovich et al. (2011), who used a Monte Carlo simulation of the interaction between the solar wind protons and the Martian atmospheric neutrals, and showed that the presence of an induced horizontal magnetic field increases the backscattering of incoming protons. This means that the downward proton flux is reduced by the magnetic field. As an example, the gyro-radius of a 2 keV proton is 1300 km in a 5 nT magnetic field (typical value at 400 km altitude in a region of weak crustal field), and becomes ~30 km in a 200 nT magnetic field (typical value at 400 km altitude in the region of the strongest anomalies). However, the magnetic field configuration, not only its magnitude, is important in determining plasma motion. In a recent study using a hybrid simulation, Brecht and Ledvina (this issue, 2012) showed that magnetic anomalies can locally focus solar wind protons into cusps. On the observational side, there is on one hand no clear evidence that magnetic anomalies actually have a significant influence on the solar wind ion dynamics in the near-Mars environment (Diéval et al., submitted, 2011; Stenberg et al., 2011). On the other hand, there is evidence that in the Southern hemisphere, the strong magnetic anomalies reduce the ionospheric ion outflow (Nilsson et al., 2011) and affect the flow pattern of escaping O+ ions (Lundin et al., 2011). The possible effect of the magnetic anomalies on proton precipitation will be investigated in a future statistical study using Mars Express observations. Although the magnetic anomalies might change the precipitation pattern, we believe that the direction of the convection electric field is a much more important parameter.
is a much more important parameter.
2.1 Input parameters: Solar wind
In our model, the solar wind contains H+ and He++ ions. Two simulations are conducted in this study. The upstream solar wind parameters are the same in both: the density is 2.5 cm−3, the bulk velocity vector is [−487, 0, 0] km s−1 and the temperature is 1.5 ∙ 105 K. This corresponds to average solar wind conditions. The aberration angle of the solar wind direction, due to the Martian orbital motion, is excluded in our study, which means that the solar wind direction is assumed to be along the Mars-Sun line. We use two different interplanetary magnetic fields (IMF). In one case, the IMF vector is [1.9, −1.6, −2.5] nT with a Parker spiral angle of 57° (Parker IMF simulation). In the second case, it is [0, 3, 0] nT (B x = 0 simulation), which means that the IMF is perpendicular to the solar wind flow. The B x = 0 case results in a symmetric draping of the IMF, which helps us to study the precipitation patterns, particularly the asymmetries with respect to the direction of the convection electric field, as will be seen later in Section 3. In the Parker spiral case, the Parker spiral leads to a draping asymmetry, which affects the plasma environment, including the precipitation patterns. This situation is more realistic. The IMF y and z components of the Parker IMF case were derived from Mars Global Surveyor (MGS) data, recorded on February 27, 2004, with the method used by Fedorov et al. (2006). The draped IMF measured by MGS is expected to have the same orientation in the y–z plane as the upstream IMF (Brain et al., 2006; Fedorov et al., 2006). This IMF data has also been used as input to the hybrid simulation performed in Diéval et al. (submitted, 2011).
2.2 Input parameters: Neutral corona
Two spherically symmetric neutral coronae (oxygen and hydrogen) around Mars are included. The hydrogen corona is a source of H+ ions and the oxygen corona is a source of O+ ions. We use the same hot hydrogen and oxygen exospheres as the ones used in the community coordinated Solar Wind Interaction with Mars (SWIM) modeling comparison team. The hydrogen neutral profile adopted into the present paper is

where N1 = 1.5∙ 1011, N2 = 1.9∙ 1010, A1 = −25965∙ 103, A2 = −10365 ∙ 103, R0 = 3593.5 ∙ 103, r is the distance from the center of Mars (in meters) and the subscript 1 and 2 refers to the thermal and hot hydrogen profiles, respectively. The cold component is from Chaufray et al. (2008). The photoionization rate is 5.58 ∙ 10−8 s−1 from Ma et al. (2004) (see also Fulle et al., 2007, for hydrogen photoionization rates), and it corresponds to solar minimum conditions.
The neutral hot oxygen profile is modeled as Eq. (4)

where N1 = 5.23 ∙ 109, N2 = 9.76 ∙ 108, N3 = 3.71 ∙ 1010, B1 = 626.2 ∙ 103, B2 = 2790 ∙ 103, B3 = 88.47 ∙ 103, R0 = 3393.5 ∙ 103, and r is the distance from the center of Mars (in meters). The photoionization rate is 8.89 ∙ 10−8 s−1 from Ma et al. (2004) (their table 1). The values of the density and photoionization rate correspond to solar minimum conditions.
2.3 Input parameters: Ionospheric ions
The HYB-Mars model does not contain self-consistent ionosphere because of the coarse grid size (minimum grid size is 180 km). Therefore, the role of ions originating from below the exobase is taken into account by emitting O+ and ions from the model inner boundary. The inner boundary, which mimics the exobase, is a spherical shell at 207 km altitude. The model also contains a background electron density, which mimics the role of the density of planetary ions. Ionospheric oxygen ions are created in the model with a dependence of the form 0.1 + 0.9 ∙ cos(SZA) on dayside, while the emission is equal to 0.1 on nightside. Radio occultation studies have shown that the peak in the electron density profiles at Mars has this SZA dependence (e.g. Zhang et al., 1990).
ions from the model inner boundary. The inner boundary, which mimics the exobase, is a spherical shell at 207 km altitude. The model also contains a background electron density, which mimics the role of the density of planetary ions. Ionospheric oxygen ions are created in the model with a dependence of the form 0.1 + 0.9 ∙ cos(SZA) on dayside, while the emission is equal to 0.1 on nightside. Radio occultation studies have shown that the peak in the electron density profiles at Mars has this SZA dependence (e.g. Zhang et al., 1990).
2.4 Input parameters: Chemical reactions
In addition to photoionization, the hybrid model also implements electron impact ionization reactions, and charge-exchange (CX) reactions between the neutral corona atoms and exospheric/solar wind protons. As in our previous study (Kallio et al., 2010), constant cross sections were used in the CX processes: 2.5 ∙ 10−19 m2 for the two H+ − Hexosphere CX processes and 1 ∙ 10−19 m2 for the two H+ − Oexosphere CX processes
and 1 ∙ 10−19 m2 for the two H+ − Oexosphere CX processes . Also, constant electron impact ionization frequencies were used for simplicity: 1.5∙10−14 m3 s−1 fore− +Hand 5.0∙10−14 m3 s−1 for e− +O processes (see Cravens et al., 1987, their figure 2, for detailed temperature-dependent electron impact ionization frequencies).
. Also, constant electron impact ionization frequencies were used for simplicity: 1.5∙10−14 m3 s−1 fore− +Hand 5.0∙10−14 m3 s−1 for e− +O processes (see Cravens et al., 1987, their figure 2, for detailed temperature-dependent electron impact ionization frequencies).
(a) Sketch showing a grid cell (rectangle on the top right), the altitudes of the exobase (solid line), inner sphere and outer sphere (dashed lines), and gyrations of protons (black circles). (b) Longitude-latitude map. The solar wind convection electric field points to the top and the component of IMF transverse to the flow points to the right. The two thick vertical black lines at longitude = ±90° indicate the terminator. The horizontal black line at latitude = 0° separates the
points to the right. The two thick vertical black lines at longitude = ±90° indicate the terminator. The horizontal black line at latitude = 0° separates the hemispheres.
hemispheres.
2.5 Ion precipitation
In this paper, we record the position , the velocity
, the velocity , the weight w
i
and the time t
i
of the hit of an ion i during a period Δt ~ 500 s. The particles are recorded on spheres (shells) of different altitudes centered at the center of Mars. For the B
x
= 0 simulation, the ions were collected on two shells: the inner sphere and the outer sphere (distance from the center of Mars r = 3636 km and 3960 km, respectively). They correspond respectively to altitudes ~240 km and 560 km. For the Parker IMF simulation, the ions were collected at the exobase (distance r = 3600 km). This choice of the exobase for the Parker IMF case and the choice of the two other shells for the B
x
= 0 case, are made for practical reasons: the B
x
= 0 simulation was realized first, to study the dependence of the precipitation pattern on altitude. The Parker IMF simulation was realized afterwards, and then the protons were collected directly at the exobase, to study the proton population actually entering the atmosphere.
, the weight w
i
and the time t
i
of the hit of an ion i during a period Δt ~ 500 s. The particles are recorded on spheres (shells) of different altitudes centered at the center of Mars. For the B
x
= 0 simulation, the ions were collected on two shells: the inner sphere and the outer sphere (distance from the center of Mars r = 3636 km and 3960 km, respectively). They correspond respectively to altitudes ~240 km and 560 km. For the Parker IMF simulation, the ions were collected at the exobase (distance r = 3600 km). This choice of the exobase for the Parker IMF case and the choice of the two other shells for the B
x
= 0 case, are made for practical reasons: the B
x
= 0 simulation was realized first, to study the dependence of the precipitation pattern on altitude. The Parker IMF simulation was realized afterwards, and then the protons were collected directly at the exobase, to study the proton population actually entering the atmosphere.
The HYB-Mars model uses an absorbing boundary condition for ions on the inner boundary. Only the ions with a downward velocity are considered in this paper. An ion hitting the exobase is immediately “removed” and really precipitates. The ions hitting the shells above are gyrating and can hit these shells several times. Then the hits on these shells with a downward velocity are used to derive a downward flux in number of hits cm−2 s−1. This flux is not a net flux but simply the downward flux of gyrating particles. In this study, we use the term “precipitation” in a general meaning of downgoing flux in the atmosphere. This is fine in the sense that we have used the same terminology for ion measurements as in the work of Diéval et al. (submitted, 2011). We can not know whether the ions recorded by Mars Express (down to ~260 km altitude) actually enter the exobase. It was assumed that these measured ions precipitate. Note that any estimate of the precipitating flux above the exobase (either measured or simulated) may lead to strong overestimate of the real flux precipitating into the atmosphere.
A schematic sketch is shown in panel 1(a): the exobase, the inner and outer spheres, a grid cell and some ion gyrations. The distance between the inner shell and the exobase is negligible, 36 km, and then the precipitation patterns will be qualitatively the same for one set of inputs. The distance between the inner and outer spheres is 324 km, which is twice the grid size (180 km, at r < 2 Rm). The grid size is thus fine enough to capture the behaviour of the precipitating particles as they go from the outer sphere down to the exobase. An ion with energy 2 keV in a 20 nT magnetic field has a gyroradius of ~324 km. Hence, in this case, the distance between the shells is 1 gyroradius ~2 grid cells. The ion H+1 has the center of gyration above the outer sphere and impacts it several times. The ion H+2 can hit the outer and inner spheres one time. The ion H+3 hits the inner boundary one time and is absorbed. When an ion hits the inner sphere, it has practically reached the exobase, as one can see on the figure. An ion with a small gyroradius under the same magnetic field (lower energy) can gyrate during a longer time from the outer sphere to the exobase before it is taken away. In the same manner, if the magnetic field increases, the ion gyroradius becomes smaller and the particle hits the spheres more times while gyrating. On the other hand, particles with a small gyroradius tend to be backscattered at high altitude by the magnetic field. It means that the height of the depletion layer (height from which the ions have no room to gyrate because they are taken away) depends on the particle energy and on the magnetic field. In reality, the ions are not immediately lost, but scattered back by the atmosphere after ion-neutral collisions (see Kallio and Barabash, 2001, their figure 2).
For this study, the flux is binned in longitude/latitude. We use a 10° resolution. To calculate the particle flux [cm−2 s−1] of all precipitating protons i on a shell of radius R over all energies between longitudes long1 and long2, and between latitudes lat1 and lat2 (longitudes and latitudes in degrees), we use the formula:

and the corresponding formula for the energy flux [eV cm−2 s−1]:

A sketch, which represents a longitude-latitude map is shown in panel 1(b). The solar wind convection electric field points to the top and the component of IMF perpendicular to the flow
points to the top and the component of IMF perpendicular to the flow points to the right. We point out that we do not use the geographic longitude and latitude, but “magnetic” longitude/latitude coordinates related to the so-called Mars Solar Electric field (MSE) Cartesian system. In this system
points to the right. We point out that we do not use the geographic longitude and latitude, but “magnetic” longitude/latitude coordinates related to the so-called Mars Solar Electric field (MSE) Cartesian system. In this system points from the center of Mars toward the Sun, along (0° longitude, 0° latitude),
points from the center of Mars toward the Sun, along (0° longitude, 0° latitude),  points along (90°, 0°) and
points along (90°, 0°) and completes the right-handed system and points along (0°, 90°). The subsolar point (0°, 0°), dayside, nightside and
completes the right-handed system and points along (0°, 90°). The subsolar point (0°, 0°), dayside, nightside and hemispheres are indicated in the figure. We also define the 90° latitude point as the
hemispheres are indicated in the figure. We also define the 90° latitude point as the pole, and the −90° latitude point as the
pole, and the −90° latitude point as the pole. The
pole. The poles correspond to horizontal lines at the top and at the bottom in panel (b).
poles correspond to horizontal lines at the top and at the bottom in panel (b).
We will also present our results in a SZA form, to simplify comparison with the figure 6 from Kallio and Janhunen (2001). To calculate the particle flux [cm−2 s−1] of all precipitating protons i on a shell of radius R over all energies for a band of SZA (SZA1 < SZA2), we use the formula

The corresponding formula for the energy flux [eV cm−2 s−1] is

Same format as Fig. 3. Inner sphere at r = 3636 km for the B x = 0 simulation.
Same format as Fig. 3. Exobase at r = 3600 km for the Parker IMF simulation.
Energy spectra of downgoing protons. The dashed lines and solid lines correspond to the outer sphere at r = 3960 km and inner sphere at r = 3636 km, respectively. The spectra are averaged in different solar zenith angle intervals. In panels (a)–(c), the black and grey lines correspond to the solar wind protons and exospheric protons, respectively, and the curves are averages over the hemispheres. In panels (d)–(f), the black, light grey and dark grey lines correspond to the
hemispheres. In panels (d)–(f), the black, light grey and dark grey lines correspond to the hemispheres and the average of both hemispheres, respectively, for all protons. The upstream solar wind spectrum is shown as a thick black line in panel (a).
hemispheres and the average of both hemispheres, respectively, for all protons. The upstream solar wind spectrum is shown as a thick black line in panel (a).
3. Results
We first look at an overview of how the Martian environment looks for the Parker IMF case. Figure 2 shows the proton density and the magnetic field strength from the Parker IMF simulation (panels (a) and (b), respectively), in the x–z plane (y = 0). The exobase is shown as a sphere originating from the center of Mars. The black shading serves to see the exobase better. The ripples at the center of the spheres occur because the grid is cubic and the quantities are derived on a sphere. Panel (a) contains contributions from all proton populations.
The density of the solar wind increases at the bow shock and decreases close to Mars on the dayside and behind Mars on the nightside (panel (a)). We see that at the exobase, the proton density is asymmetric in z on the dayside. This is related to the direction of the solar wind convection electric field, which points predominantly toward the z < 0 region (the y component of the IMF is negative) for this simulation. The magnetic field increases first at the bow shock, and continues to increase closer to the planet, forming the magnetic barrier (panel (b)). The magnetic barrier is stronger in the z < 0 region, and the maximum magnetic field is not at subsolar point. It was shown in hybrid simulations (e.g. Brecht, 1990) that the magnetic pile-up in the magnetic barrier is stronger on the hemisphere where the solar wind convection electric field points away from the planet. We can also see that the plasma boundaries are asymmetric with respect to the x-axis, especially in the tail.
3.1 Precipitation map on the outer sphere: Perpendicular IMF case
We will now focus on the proton precipitation patterns resulting from the two simulations. We first consider the B
x
= 0 simulation since it is the simplest case and we investigate how the precipitation pattern changes with distance to Mars. We start with the pattern recorded on the outer sphere at r = 3960 km, which is shown in Fig. 3 (panel (a)), in unit of log10(hits cm−2 s−1). The white color indicates no particles. Panel (a) shows the downgoing protons of both exospheric and solar wind origins. The pattern is symmetric about the line at 0° longitude, which separates the magnetic dawn and dusk sides. The flux is the most intense at subsolar point. The well known asymmetry related to is visible, with a more intense flux in the direction aligned with the convection electric field (
is visible, with a more intense flux in the direction aligned with the convection electric field ( hemisphere) than in the opposite direction (
hemisphere) than in the opposite direction ( hemisphere). Precipitation also exists on the nightside. All these features are in agreement with Brecht (1997) and Kallio and Janhunen (2001). The reader can find the values of energy and particle fluxes in Section 4, where the results from the different altitudes are summarized.
hemisphere). Precipitation also exists on the nightside. All these features are in agreement with Brecht (1997) and Kallio and Janhunen (2001). The reader can find the values of energy and particle fluxes in Section 4, where the results from the different altitudes are summarized.
We are also interested to separate the contribution from solar wind and planetary origins (panels 3(b) and (c)). In the simulation we record different planetary proton species on the shells: photoions, protons created by electron impact ionization, and protons created by a CX reaction between a solar wind proton and a neutral hydrogen atom. In our analysis, we group them together into one exospheric population. We see that for both solar wind and planetary protons (panels (b) and (c)), the most intense flux is at the subsolar point, and the flux onto the hemisphere is larger than in the
hemisphere is larger than in the hemisphere. The planetary proton flux is more intense than the solar wind flux on the
hemisphere. The planetary proton flux is more intense than the solar wind flux on the hemisphere. On the
hemisphere. On the hemisphere, there are several interesting features. One is that the exospheric proton flux is higher on the flanks of the region of major deposition, than in the center (it makes an orange “V” shape in panel (c)). Another thing to note is that around the
hemisphere, there are several interesting features. One is that the exospheric proton flux is higher on the flanks of the region of major deposition, than in the center (it makes an orange “V” shape in panel (c)). Another thing to note is that around the pole (~90° latitude), the solar wind flux is higher than the exospheric flux. However, the planetary flux is higher than the solar wind flux away from the
pole (~90° latitude), the solar wind flux is higher than the exospheric flux. However, the planetary flux is higher than the solar wind flux away from the pole, on the nightside along a curve (yellow-green on panel (c)) starting at the terminator and arriving at the antisubsolar point (−180°/180°, 0°). Finally, there are two “patches” on the nightside flanks, touching both the
pole, on the nightside along a curve (yellow-green on panel (c)) starting at the terminator and arriving at the antisubsolar point (−180°/180°, 0°). Finally, there are two “patches” on the nightside flanks, touching both the hemispheres, symmetric relative to the 0° longitude line, where the flux is quite high: one region from − 135° to −90° longitude and from −45° to 45° latitude (magnetic dawn), the other is on the other side (magnetic dusk). In these two regions (blue-green in panel (b)), the planetary protons also dominate. These “patches” correspond to the regions where the transverse component of the IMF
hemispheres, symmetric relative to the 0° longitude line, where the flux is quite high: one region from − 135° to −90° longitude and from −45° to 45° latitude (magnetic dawn), the other is on the other side (magnetic dusk). In these two regions (blue-green in panel (b)), the planetary protons also dominate. These “patches” correspond to the regions where the transverse component of the IMF points toward/away from Mars. Generally, on the nightside and away from the convection electric field direction, the planetary protons dominate the solar wind protons. The flux differences between different regions are smaller, i.e. the pattern is more uniform, for planetary protons than for solar wind protons. The incoming solar wind protons have a strongly asymmetric deposition pattern and precipitate intensively in the region aligned with
points toward/away from Mars. Generally, on the nightside and away from the convection electric field direction, the planetary protons dominate the solar wind protons. The flux differences between different regions are smaller, i.e. the pattern is more uniform, for planetary protons than for solar wind protons. The incoming solar wind protons have a strongly asymmetric deposition pattern and precipitate intensively in the region aligned with direction and in the subsolar point.
direction and in the subsolar point.
Now we instead divide the protons into different energy ranges (panels (d)–(f)). It is seen that the high energy protons avoid the hemisphere (panel (d)). In the region of major deposition, in the
hemisphere (panel (d)). In the region of major deposition, in the hemisphere, the contribution from protons of intermediate energy (panel (e)) is the most important, particularly around the
hemisphere, the contribution from protons of intermediate energy (panel (e)) is the most important, particularly around the pole and at the subsolar point. We observe that the
pole and at the subsolar point. We observe that the hemisphere is dominated by low energy particles (panel (f)). Brecht (1997) showed that the precipitation of slow solar wind streams, i.e. low energy protons, is favored in the
hemisphere is dominated by low energy particles (panel (f)). Brecht (1997) showed that the precipitation of slow solar wind streams, i.e. low energy protons, is favored in the hemisphere; this is in agreement with our results. The symmetric “curves” and the magnetic dawn/dusk “patches” noted previously on the nightside flanks are dominated by low energy protons (panel (f)). The low energy proton flux (panel (f)) is higher than the high energy proton flux (panel (d)) in the
hemisphere; this is in agreement with our results. The symmetric “curves” and the magnetic dawn/dusk “patches” noted previously on the nightside flanks are dominated by low energy protons (panel (f)). The low energy proton flux (panel (f)) is higher than the high energy proton flux (panel (d)) in the direction. In that respect, the low energy proton contribution to the region of major deposition is significant. According to Kallio and Janhunen (2001), the
direction. In that respect, the low energy proton contribution to the region of major deposition is significant. According to Kallio and Janhunen (2001), the hemisphere favors the precipitation of low energy solar wind protons, while the
hemisphere favors the precipitation of low energy solar wind protons, while the hemisphere favors the precipitation of solar wind protons of higher energy; this is in agreement with our results. It seems that the low energy features are associated with the exospheric protons. This hypothesis is verified later in Fig. 6.
hemisphere favors the precipitation of solar wind protons of higher energy; this is in agreement with our results. It seems that the low energy features are associated with the exospheric protons. This hypothesis is verified later in Fig. 6.
3.2 Precipitation map on the inner sphere: Perpendicular IMF case
Next, we study the downgoing particles at a lower altitude. Figure 4 presents the precipitation patterns on the inner sphere at r = 3636 km. Compared to Fig. 3, the deposited flux has decreased everywhere. In panel 4(a), compared to panel 3(a), the flux is decreased by 2–3 orders of magnitude at subsolar point (0°, 0°) and by less than one order of magnitude at the and
and poles and at the anti-subsolar point. The region of major deposition shrinks and becomes narrower. The flux is still more intense in the
poles and at the anti-subsolar point. The region of major deposition shrinks and becomes narrower. The flux is still more intense in the direction and around the
direction and around the pole (panel (a)). The flux at the subsolar point is now smaller than at the
pole (panel (a)). The flux at the subsolar point is now smaller than at the pole, and is comparable to the flux at the
pole, and is comparable to the flux at the pole.
pole.
Next we compare the different proton species (panels (b) and (c)). We see that, again, the solar wind protons dominate the pole and the rest of the major deposition region (panel (b)), while the exospheric protons dominate the
pole and the rest of the major deposition region (panel (b)), while the exospheric protons dominate the hemisphere (panel (c)). The symmetric “curves” on the nightside flanks, noted in panel 3(c), disappear in panel 4(c). But the magnetic dawn/dusk “patches” are still visible.
hemisphere (panel (c)). The symmetric “curves” on the nightside flanks, noted in panel 3(c), disappear in panel 4(c). But the magnetic dawn/dusk “patches” are still visible.
The contribution of protons of different energies is shown in panels (d)–(f). We see that the flux of the low energy protons now concentrates at the pole and has decreased significantly in the rest of the region of major deposition, especially at the subsolar point (panel (f)). The region of major deposition is again dominated by the protons of intermediate energies (panel (c)). The
pole and has decreased significantly in the rest of the region of major deposition, especially at the subsolar point (panel (f)). The region of major deposition is again dominated by the protons of intermediate energies (panel (c)). The hemisphere is favored by the low energy protons (panel (f)) and avoided by the high energy protons (panel (d)). Thus, when looking closer to Mars (here, only 36 km above the exobase) the region of major deposition tends to shrink, becoming more strongly aligned with the convection electric field direction and moves away from the subsolar point, to favor the
hemisphere is favored by the low energy protons (panel (f)) and avoided by the high energy protons (panel (d)). Thus, when looking closer to Mars (here, only 36 km above the exobase) the region of major deposition tends to shrink, becoming more strongly aligned with the convection electric field direction and moves away from the subsolar point, to favor the pole.
pole.
The precipitation pattern on the inner sphere differs from the results of Brecht (1997) and Kallio and Janhunen (2001). Indeed, they show that the precipitating flux is largest at low SZA. In the former study, the flux was derived at the surface of Mars. Unfortunately, the latter study does not mention the altitude at which the fluxes were calculated, but it is probably the exobase. A comparison will be made in Section 4. The dramatic change of the precipitation pattern when approaching Mars, suggests that the subsolar region may be strongly affected by some process, which reduces the downward flux in that region. The nature of this process will be examined in Section 4.
3.3 Precipitation map on the exobase: Parker spiral case
Moving further down, we get to the exobase. The ions which have reached this altitude (207 km) will hit the inner boundary once, be absorbed in the atmosphere and not gyrate out again. The corresponding flux is thus the particle precipitation in its original meaning. The altitude difference between the exobase and the inner sphere is small. The two patterns will thus be qualitatively similar for a given set of inputs.
Next, we will look at the effect of the Parker spiral on the precipitation patterns. We show the precipitation map at the exobase in Fig. 5. The main features found in the B
x
= 0 case are also visible in Fig. 5. But the details in the patterns differ. The poles, the major deposition region, and the magnetic dawn/dusk patches on the nightside flanks are now asymmetric about the 0° longitude line. The flux is more intense on the magnetic dawn patch from −135° to −90° longitude (orange) than on the magnetic dusk patch from 90° to 135° longitude (green) in panel (a). In other words, the flux is higher in the region where
poles, the major deposition region, and the magnetic dawn/dusk patches on the nightside flanks are now asymmetric about the 0° longitude line. The flux is more intense on the magnetic dawn patch from −135° to −90° longitude (orange) than on the magnetic dusk patch from 90° to 135° longitude (green) in panel (a). In other words, the flux is higher in the region where points toward Mars, than in the region where it points away. This is consistent with the work of Dubinin et al. (2008). They indeed show that the induced magnetosphere of Mars is more exposed to solar wind protons on the side where the upstream IMF vector points toward the planet than on the opposite side. Around the
points toward Mars, than in the region where it points away. This is consistent with the work of Dubinin et al. (2008). They indeed show that the induced magnetosphere of Mars is more exposed to solar wind protons on the side where the upstream IMF vector points toward the planet than on the opposite side. Around the pole, the pattern is irregular on the dawn side, and more regular on the dusk side, and the flux is higher on the dusk side of the
pole, the pattern is irregular on the dawn side, and more regular on the dusk side, and the flux is higher on the dusk side of the pole than on the dawn side (panel (a)). Around the
pole than on the dawn side (panel (a)). Around the pole, the opposite is true: the pattern is more regular on the dawn side, and irregular on the dusk side. These dawn-dusk asymmetries are seen in the two maps of solar wind protons and planetary protons as well (panel (b) and (c)), and also for different energy ranges (panels (d)–(f)). Thus, the Parker spiral makes the precipitation pattern more complicated. Finally, when looking at the subsolar point (0°, 0°) at different altitudes, we see that the solar wind protons dominate the precipitating flux at high altitude (Fig. 3), while the exospheric protons become significant at lower altitude (Fig. 5).
pole, the opposite is true: the pattern is more regular on the dawn side, and irregular on the dusk side. These dawn-dusk asymmetries are seen in the two maps of solar wind protons and planetary protons as well (panel (b) and (c)), and also for different energy ranges (panels (d)–(f)). Thus, the Parker spiral makes the precipitation pattern more complicated. Finally, when looking at the subsolar point (0°, 0°) at different altitudes, we see that the solar wind protons dominate the precipitating flux at high altitude (Fig. 3), while the exospheric protons become significant at lower altitude (Fig. 5).
3.4 Precipitating proton spectra
We have also derived precipitating proton spectra on the outer and inner spheres, to check the altitude dependence. We return to the simple B x = 0 case. The spectra are shown in Fig. 6. The energy flux is plotted for three SZA ranges: 0°−60° (subsolar region), 60°−120° (terminator region) and 120°−180° (nightside). The dashed lines correspond to the outer sphere (560 km altitude) and the solid lines to the inner sphere (240 km altitude). The thick black curve is the upstream solar wind spectrum used as input: a Maxwellian distribution which peaks at ~ 1.2 keV.
3.4.1 Solar wind and planetary protons contributions
In the first row we compare the contribution from the solar wind protons (black) and planetary protons (grey) to the precipitating spectra. The spectra are averaged over the hemispheres.
hemispheres.
The energy fluxes decrease as we go from the outer sphere to the inner sphere. It drops more drastically at low energy (E < 100 eV) than at higher energy, when the altitude decreases. One can also see that the decrease at E < 100 eV is larger in the subsolar region (panel (a)) than at higher SZA. The peak in the energy spectra is well pronounced in the subsolar region (panel (a)), and vanishes as we go to the terminator (panel (b)) and the nightside (panel (c)). The energy peak is also more pronounced at low altitude than at high altitude, for a given spatial region. The energy peak also shifts to higher energy as we go down in altitude on dayside (panel (a)). One can see that the low energy part (E < 100 eV) is dominated by cold new-born planetary protons. The domination of the low energy population by the planetary protons becomes more evident as the altitude decreases in the subsolar region (panel (a)). By contrast, the domination of the low energy population by the planetary protons becomes less evident as the altitude decreases for the terminator and nightside (panels (b) and (c)). On the outer sphere, indeed, the exospheric proton peak level is by contrast higher than the solar wind peak on nightside (panel (c)). The higher energy part (E > 400 eV) is dominated by solar wind protons until 4–5 keV; above this energy, the spectrum becomes dominated again by the planetary protons, accelerated by the convection electric field. The solar wind spectrum peaks at a higher energy and at a higher level than the planetary proton spectrum, on the dayside and at the terminator (panels (a) and (b)).
On the outer sphere, the spectrum of solar wind protons peaks at a lower energy than the upstream solar wind, but on the inner sphere, it peaks at a higher energy than the upstream solar wind (panels (a) and (b)). On the outer sphere, the exospheric proton spectrum also peaks at an energy lower than the upstream solar wind, but on the inner sphere, it peaks at the same energy as the upstream solar wind (panels (a) and (b)). On the dayside, the precipitating solar wind spectrum energy peak is at ~2 ∙ 107 eV cm−2 s−1 eV−1 on the outer sphere and is ~ 1 ∙ 106 eV cm−2 s−1 eV−1 on the inner sphere (panel (a)), respectively 1 and 2 orders of magnitude lower than the upstream solar wind energy flux (4 ∙ 108 eV cm−2 s−1 eV−1). The precipitating solar wind spectrum, averaged over a given sphere, would peak at the mean energy of the upstream solar wind.
The flux decrease seen at low energy is more drastic in the subsolar region when the altitude decreases. On the dayside, the high energy population accelerates as we approach Mars. This can be related to the removal of the low energy population. The low energy population tends to be dominated by planetary protons. On the dayside, the contribution of the planetary protons to the low energy population is, relatively to the solar wind, larger at lower altitudes than at high altitudes, because new-born planetary protons are massively created at lower altitudes in the corona on the dayside. At the terminator and on the nightside, the reverse is true: the contribution of the planetary protons to the low energy population is, relatively to the solar wind, lower at low altitudes than at high altitudes. This is because it is difficult to create planetary protons at low altitude in Mars’s shadow. At very high energies (above 4–5 keV), the contribution of planetary protons to the precipitation becomes more important than that of the solar wind. The planetary population has been accelerated by the convection electric field. The maximum energy gain is 4Esw(sin(θ))2, where Esw is the upstream solar wind bulk energy and θ is the angle between the solar wind velocity and the IMF. For this simulation, θ = 90° and Esw ~ 1.2 keV, so the maximum energy gain is ~5 keV. Planetary protons are also seen with even higher energies (bump around 10 keV). We interpret these exospheric protons with energies more than 4Esw as protons picked up upstream of the bow shock and accelerated by reflections at the Martian bow shock (Dubinin et al., 2006). Test-particle simulations (e.g. Dubinin et al., 1994), which follow the ions motion under electromagnetic fields, have shown that exospheric picked up protons are reflected by the bow shock potential. In principle, hybrid simulations, which also treat ions as particles, can model how some of the ions are accelerated and scattered at the bow shock back to the upstream solar wind.
3.4.2 Energy spectra organized by the convection electric field
In the second row of Fig. 6, we investigate the relationships between the precipitating proton spectra and the hemispheres. The panels (d), (e) and (f) show the energy spectra, in the same format as in panels (a)–(c), but for the
hemispheres. The panels (d), (e) and (f) show the energy spectra, in the same format as in panels (a)–(c), but for the hemisphere (black), the
hemisphere (black), the hemisphere (light grey) and the average (dark grey). These spectra correspond to all protons (solar wind and exospheric origins).
hemisphere (light grey) and the average (dark grey). These spectra correspond to all protons (solar wind and exospheric origins).
The two populations together cause the average spectrum on the outer sphere to peak at an energy flux comparable (1 ∙ 108 eV cm−2 s−1 eV−1) to the solar wind energy peak on dayside (panel (d)). At the terminator and on the night-side (panels (e) and (f)), the peak is lower. On the inner shell, the asymmetry is the most pronounced on the dayside (panel (d)), and least pronounced on the nightside (panel (f)). On the outer shell, the
asymmetry is the most pronounced on the dayside (panel (d)), and least pronounced on the nightside (panel (f)). On the outer shell, the asymmetry is most pronounced at the terminator (panel (e)). This is consistent with the strong
asymmetry is most pronounced at the terminator (panel (e)). This is consistent with the strong hemisphere asymmetry noticed in Fig. 3. On the inner shell, the peak of the energy spectrum on the
hemisphere asymmetry noticed in Fig. 3. On the inner shell, the peak of the energy spectrum on the hemisphere exists on dayside (panel (d)), but disappears at the terminator and on the nightside (panels (e) and (f)). On the inner shell, the peak in the
hemisphere exists on dayside (panel (d)), but disappears at the terminator and on the nightside (panels (e) and (f)). On the inner shell, the peak in the hemisphere spectrum persists on the dayside and the terminator (panels (d) and (e)).
hemisphere spectrum persists on the dayside and the terminator (panels (d) and (e)).
On the inner shell, the low energy population plays a dominant role in the hemisphere spectrum. Also, on the inner shell on the dayside and at the terminator (panels (d) and (e)), the
hemisphere spectrum. Also, on the inner shell on the dayside and at the terminator (panels (d) and (e)), the hemisphere spectrum gets a significant contribution from both the low energy population and the higher energy population, which have their own preferred area of deposition (see panels 4(d)–(f)).
hemisphere spectrum gets a significant contribution from both the low energy population and the higher energy population, which have their own preferred area of deposition (see panels 4(d)–(f)).
The average precipitating spectrum is dominated by protons of energy greater than a few hundred eV, in qualitative agreement with studies of Brecht (1997) and Kallio and Janhunen (2001).
4. Discussion
The analysis shows that the energy and particle proton fluxes (solar wind and exospheric origins together), which reach the exobase on the dayside are ~9.3 ∙ 1026 eV s−1 and ~6.4 ∙ 1023 H+ s−1, respectively. If only solar wind protons are taken into account, the energy flux is ~7.7 ∙ 1026 eV s−1 and the particle flux is ~4.0 ∙ 1023 H+ s−1. Thus, the solar wind protons account for 62% of the precipitating proton flux on dayside on the inner boundary. We can consider separately the low energy and the higher energy populations. Taking all protons with energies below the solar wind bulk energy, the planetary protons account for 55% and the solar wind protons for 45% of the precipitating population at the inner boundary. When taking all protons with energies above the solar wind bulk energy, the two populations account for 27% and 73% of the population, respectively.
These precipitating energy and particle fluxes of solar wind protons correspond respectively to ~ 1% of the energy flux and ~ 1% of the particle flux of the upstream solar wind protons (if the upstream solar wind could directly hit the exobase).
Now, we compare our results expressed in a SZA form, with the figure 6 from Kallio and Janhunen (2001). We use a 15° resolution. The precipitating proton flux, averaged over the hemispheres, is shown as a function of SZA in Fig. 7. All protons are considered: solar wind and exospheric origins. The particle flux (panel (a)) and energy flux (panel (b)) are summarized at the exobase in the Parker spiral case at 207 km altitude (solid line with crosses), the inner sphere at 240 km altitude (solid line) and outer sphere at 560 km altitude (dashed line) in the B
x
= 0 case. This way of presenting the precipitating flux washes out the eventual dawn-dusk asymmetries. The reader has to keep in mind that the flux that would be derived at the exobase for the B
x
= 0 case would be slightly different from the flux shown by the solid-and-crosses line, because of different IMF magnitudes (3 nT and 3.5 nT for the B
x
= 0 and Parker IMF cases respectively).
hemispheres, is shown as a function of SZA in Fig. 7. All protons are considered: solar wind and exospheric origins. The particle flux (panel (a)) and energy flux (panel (b)) are summarized at the exobase in the Parker spiral case at 207 km altitude (solid line with crosses), the inner sphere at 240 km altitude (solid line) and outer sphere at 560 km altitude (dashed line) in the B
x
= 0 case. This way of presenting the precipitating flux washes out the eventual dawn-dusk asymmetries. The reader has to keep in mind that the flux that would be derived at the exobase for the B
x
= 0 case would be slightly different from the flux shown by the solid-and-crosses line, because of different IMF magnitudes (3 nT and 3.5 nT for the B
x
= 0 and Parker IMF cases respectively).
Precipitating proton particle flux (panel (a)) and energy flux (panel (b)) function of SZA. The fluxes are averaged over the hemispheres. The outer sphere at r = 3960 km (dashed line), the inner sphere at r = 3636 km (solid line) for the B
x
= 0 case are shown, as well as the exobase at r = 3600 km for the Parker IMF case (solid line and crosses).
hemispheres. The outer sphere at r = 3960 km (dashed line), the inner sphere at r = 3636 km (solid line) for the B
x
= 0 case are shown, as well as the exobase at r = 3600 km for the Parker IMF case (solid line and crosses).
On the outer sphere, the flux is largest at subsolar point (~3 ∙ 108 hits cm−2 s−1 and ~3 ∙ 1011 eV cm−2 s−1) and decreases toward the nightside. On the outer sphere, at the terminator, the fluxes are ~3∙ 107 hits cm−2s−1 and ~2∙ 1010 eV cm−2 s−1. The flux values at subsolar point on the outer sphere are larger than the upstream solar wind particle flux (~1 ∙ 108 H+ cm−2 s−1) and energy flux (~2 ∙ 1011 eV cm−2 s−1). However, this is not a problem since the flux on the outer sphere contains contributions from both the solar wind and the planetary protons. It implies that the exospheric proton production is significant at low SZA, and that it locally contributes to the precipitation.
The overall flux has decreased, by one order of magnitude at the terminator and nightside and by 2 orders of magnitude on the dayside when we reach the inner sphere. On the inner sphere, the particle flux is ~1 ∙ 106 hits cm−2 s−1 and the energy flux is ~1 ∙ 109 eV cm−2 s−1 at the subsolar point, while they reach ~2 ∙ 106 hits cm−2 s−1 and ~2 ∙ 109 eV cm−2 s−1 respectively at the terminator.
At the exobase, there is a small change in flux compared to the inner sphere on the nightside and at the terminator, but on the dayside, the flux again decreases by one order of magnitude. At the exobase, the fluxes become ~1 ∙ 105 H+ cm−2 s−1 and~1∙108 eVcm−2 s−1 at the subsolar point, and ~1 ∙ 106 H+ cm−2 s−1 and ~1 ∙ 109 eV cm−2 s−1 at the terminator. Hence, at the inner boundary, the fluxes (solar wind and planetary protons combined) have decreased by 3 orders of magnitude compared to the upstream solar wind.
Our results show differences compared to the work by Kallio and Janhunen (2001). Our integrated precipitating proton particle flux at the exobase is about 1% of the total solar wind flux, while they get almost 50%. In contrast to their paper, our proton fluxes are also severely reduced at the subsolar point close to Mars. At the subsolar point our precipitating particle fluxes are up to 3 orders of magnitude lower than the fluxes shown by Kallio and Janhunen (2001). Finally, we note that our energy fluxes on the dayside are comparable to what is obtained by Brecht (1997), except in the subsolar region where he gets an energy flux value of ž1 ∙ 109 eV cm−2 s−1 for nominal solar wind conditions.
There are several possible reasons for these differences. The solar wind input parameters are not a likely reason, because Kallio and Janhunen (2001) used a solar wind bulk velocity quite similar to ours (they used [−400, 0, 0] km s−1), while the solar wind density and the IMF were identical to ours for the B x = 0 simulation. In the previous work, the neutral oxygen corona was spherically symmetric like ours, but had a scale height of 1100 km and a manually given O+ photoionization production rate within the simulation box of ~6 ∙ 1023 s−1. In the present work, the oxygen corona is modeled by three scale heights and the ion production rate is derived by using a photoionization rate (see Section 2). Planetary ions, which are originating from the ionosphere, are also modeled in a more realistic way than by Kallio and Janhunen (2001). In our study, the emission has a cos(SZA) dependence while in their study the ions were emitted homogeneously on the dayside. The cos(SZA) dependence increases the relative density of planetary ions near the subsolar point compared to the previous study, which may also affect the strength of the magnetic barrier and the properties of the ion composition boundary, which separates the solar wind and planetary ions. In this study, the model also contains background electron density, which mimics the role of the density of planetary ions that are not included in the hybrid model.
We note that neither the current model nor the 2001 study contain a self-consistent ionosphere, but they both have a changing grid size as the altitude decreases (with similar grid sizes in both codes). Hence, these two features do not explain the differences in the results for low altitude.
The number of particles per cell is increased in the present study. In addition, the numerical code used in the present work gives a much less disturbed magnetic barrier near the grid refined boundaries and a more clearly defined bow shock (see Fig. 2) than in the old numerical code used by Kallio and Janhunen (2001). We also note that the size of the region where the magnetic field magnitude is high (>20 nT) is larger and the proton density near Mars is smaller, compared with the previous work. The reduced proton density, resulting from a stronger magnetic barrier and a stronger bow shock, should result in fewer protons reaching the exobase.
The new model also includes processes that were not included in the previous work: charge exchange reactions between protons and neutral atoms, and electron impact ionization. The electron impact ionization reactions and the charge exchange reactions between the neutral exospheric atoms and the solar wind plasma play in an important role in the formation of the Martian plasma boundaries, in particular the magnetic barrier (Jin et al., 2006). This shows the necessity to implement exospheric processes.
It is said before that 62% of the proton deposition on dayside comes from the solar wind; the rest comes from the exosphere. The photoionization and the electron impact ionization create additional exospheric protons, but do not necessarily result in an increased precipitation since these ions are created with low energies and small gyroradii. The charge exchange of the solar wind protons with neutral hydrogen does not change the number of protons. It replaces relatively high energy solar wind protons by new-born cold exospheric ions which are less likely to pass the magnetic barrier on dayside. These cold ions are then picked up and accelerated by the solar wind convection electric field, and may again charge exchange with the neutral coronae, giving either new-born exospheric protons or O+ ions. The same reasoning applies to the charge exchange of the exospheric protons with the coronae.
The charge exchange of the incoming protons with the neutral atoms of the oxygen corona accounts for a part of the removal of the proton population at low SZA. For example, if the density of the neutral coronas is high, then the charge exchange of the solar wind with the low altitude oxygen corona can attenuate the proton density by a few tens of percent in the subsolar region close to the obstacle (Kallio et al., 1997). In the model, the high production rate of oxygen ions at low SZA leads to a region dominated by planetary ions. A so-called Ion Composition Boundary forms, which separates the oxygen plasma and the incoming protons. Note that the mass loading of the solar wind flow by the O+ ions from the oxygen corona will also push the bow shock further from Mars, reducing the proton precipitation (Kallio and Janhunen, 2001). It is noted that only an oxygen corona was present in the study by Kallio and Janhunen (2001), while the present study uses both oxygen and hydrogen coronae. The presence of both exospheres in the new model may slow down the solar wind more strongly. One consequence is that the decelerated solar wind protons have smaller gyroradii and do not penetrate the magnetic barrier as effectively.
Both our model and the model used by Kallio and Janhunen (2001) have an absorbing boundary condition for the inner boundary. Thus, the incoming protons are not reflected, but absorbed. In the paper by Kallio and Janhunen (2001), a hybrid code is used above the exobase, and a Monte Carlo simulation is used below. This means that in their model, the protons are not artificially cut away from the whole simulation, but are treated as particles colliding with atmospheric neutrals. These collisions backscatter the ions (Kallio and Barabash, 2001). The ions may hit the inner boundary a few times more, instead of being immediately removed after one hit on the inner boundary. We cannot completely exclude the effect of the particle removal introduced by our inner boundary (see Fig. 1) on the precipitation pattern at altitudes lower than the outer sphere. However, this removal should be in proportion to the number of particle hits onto the exobase. In the case where the ions are taken away when hitting the inner boundary, one would expect that if the number of incoming particles to the exobase is larger on the dayside than elsewhere, the inner boundary will remove the hits in the same proportion all over the planet. On the other hand, if ion-neutral collisions are implemented at the exobase, one would also expect that if the incoming proton flux is largest on dayside, the proton flux at the exobase will be still largest in that region, after particle backscattering.
Our analysis suggests that a process is removing protons at low altitude on the dayside, between the outer sphere and the exobase. This geographically localized removal of protons cannot be explained by the way the protons are treated at the exobase (either cut away from the simulation or scattered by collisions). We think that this process is due to the finite gyroradius effect.
The strong magnetic field in the magnetic barrier, especially at low SZA, can deflect H+ ions with a small gyroradius, preventing them from reaching the exobase. For instance, at the altitude of the exobase, the magnetic field from the simulation has a value of ~45 nT at low SZA. In this field, a 100 eV proton has a gyroradius of 32 km, while a 5000 eV proton has a gyroradius of 227 km. This can be compared to the size of the region where the magnetic field magnitude is largest: ~500 km at low SZA (panel 2(b)). It is noted that the inner sphere (240 km altitude) is located inside the magnetic barrier, while the outer sphere is located slightly above (560 km altitude). The low energy protons, which have passed the altitude of the outer sphere will thus enter the magnetic barrier, where they can be deflected and only a few reach this region. As the SZA increases, the magnetic field magnitude decreases and the access becomes easier for low energy protons, as seen in the proton maps. This interpretation is supported by the work of Shematovich et al. (2011). As said in Section 2, they showed that the stronger the induced magnetic field in the Martian atmosphere, the more incoming solar wind protons is backscattered. They found that a 50 nT horizontal magnetic field (typical value measured in the magnetic barrier) shields almost completely the atmosphere from downward proton fluxes. In addition, the morphology of the magnetic field on the dayside and on the nightside is not similar. On the dayside there is an horizontal magnetic field in a wide altitude range (the magnetic barrier) while on the night-side the magnetic field starts to form the magnetic tail lobes where the B
x
-component (and, consequently, vertical ) is important. Therefore, the motion of ions toward Mars (easily along
) is important. Therefore, the motion of ions toward Mars (easily along and difficult perpendicular to
and difficult perpendicular to ) is not identical at the dayside and nightside.
) is not identical at the dayside and nightside.
Now, we discuss the effect of the energy of the precipitating protons on the asymmetry. It is seen from the proton maps that at low altitude on the dayside, the low energy protons dominate the precipitation onto the
asymmetry. It is seen from the proton maps that at low altitude on the dayside, the low energy protons dominate the precipitation onto the hemisphere while the precipitation onto the
hemisphere while the precipitation onto the hemisphere is dominated by protons with higher energies. This can be explained by the Lorentz force. In Eq. (2), the pressure gradient term is of minor importance for the precipitating protons in the energy range analyzed in this study. Only the
hemisphere is dominated by protons with higher energies. This can be explained by the Lorentz force. In Eq. (2), the pressure gradient term is of minor importance for the precipitating protons in the energy range analyzed in this study. Only the and
and terms need to be considered. The proton velocity
terms need to be considered. The proton velocity can differ from the electrons bulk velocity
can differ from the electrons bulk velocity in all regions where there is a substantial amount of oxygen ions (i.e. where the mass loading is important) and where there are strong electric currents (like in the cross tail current sheet). The low energy protons (velocity
in all regions where there is a substantial amount of oxygen ions (i.e. where the mass loading is important) and where there are strong electric currents (like in the cross tail current sheet). The low energy protons (velocity ) are affected by the
) are affected by the electric field which accelerates them toward Mars on the
electric field which accelerates them toward Mars on the hemisphere. The higher energy protons (velocity
hemisphere. The higher energy protons (velocity ) are affected by the
) are affected by the electric field which accelerates them toward Mars on the
electric field which accelerates them toward Mars on the hemisphere (Kallio and Janhunen, 2001). Recalling that the draped magnetic field is stronger on the side of the planet aligned with the solar wind convection electric field (
hemisphere (Kallio and Janhunen, 2001). Recalling that the draped magnetic field is stronger on the side of the planet aligned with the solar wind convection electric field ( hemisphere), one may think that it is difficult for low energy protons to be deposited on the
hemisphere), one may think that it is difficult for low energy protons to be deposited on the hemisphere, because of their small gyroradius.
hemisphere, because of their small gyroradius.
The low energy population is dominated by the pickup planetary protons. Ions created very close to the exobase will have not much room to be accelerated until they reach the inner boundary. These ions are recorded as a very low energy population at the exobase. They precipitate locally, close to their place of production. On the other hand, planetary protons created upstream from the bow shock have space to gyrate. They will be accelerated and produce a more asymmetric precipitation pattern. As a consequence, the asymmetry on dayside is reduced for the low energy population, but enhanced for the higher energy population.
asymmetry on dayside is reduced for the low energy population, but enhanced for the higher energy population.
On the nightside, the magnetic field is weaker and the field lines extend vertically (tailward), such that the low energy protons can propagate more easily to low altitude. The low values of and
and , and the situation of a bulk velocity parallel with the magnetic field lines
, and the situation of a bulk velocity parallel with the magnetic field lines , decrease the convection electric field
, decrease the convection electric field on the nightside (e.g. Kallio et al., 2010). This allows the protons to move more freely, and that may be the reason for the reduction of the
on the nightside (e.g. Kallio et al., 2010). This allows the protons to move more freely, and that may be the reason for the reduction of the asymmetry on the inner sphere on the nightside.
asymmetry on the inner sphere on the nightside.
The precipitating protons deposit energy into the atmosphere, but the atmosphere also absorbs energy from the solar radiation. To compare the two energy sources, we note that the solar radiation absorption at Mars for solar minimum conditions (height-integrated in the altitude range 100−240 km) is 1.35∙1011 eVcm−2 s−1 (Kallio et al., 1997). The average precipitating energy flux from our model is ~1 ∙ 108 eV cm−2 s−1 at subsolar point at the exobase. Hence, we conclude that the energy transfer to the dayside exobase from the precipitating protons is up to 3 orders of magnitude less than the energy transfer from solar radiation absorption. Under the conditions specified for the simulation, the precipitating proton energy flux can not compete with the energy flux from the solar radiation on the day-side. On the nightside, the atmosphere is in the shadow and the proton precipitation heating becomes more important than the solar heating, in agreement with Brecht (1997) and Kallio and Janhunen (2001).
In the future, the present results should be compared to an observational statistical study of proton precipitation, which is now in progress, but this comparison is saved for a future publication.
5. Summary and Conclusions
This paper reports the first investigation of the altitude dependence of the pattern of proton precipitation onto the Martian atmosphere, using the HYB-Mars hybrid code. We also report the first study of the relative importance of solar wind versus planetary protons in term of proton precipitation, and emphasize the role of the proton energy to determine the precipitation pattern.
Overall, our study confirms the asymmetry of the proton precipitation due to the convection electric field, and its role in the energy balance compared to the UV flux, shown by Brecht (1997) and Kallio and Janhunen (2001). An important new finding is the strong altitude dependence of the proton precipitation: the flux of precipitating protons is reduced substantially when crossing the magnetic barrier near Mars. The study suggests that the Martian induced magnetosphere protects the upper atmosphere effectively against proton precipitation. Finally, we find that the solar wind protons contribute to 62% of the proton precipitation on the dayside exobase in our simulation, which means that the hydrogen exosphere can be a significant source of precipitating protons.
Concerning the atmospheric energy balance, we note that on the dayside the energy transfer to the Martian atmosphere from proton precipitation is up to 3 orders of magnitude lower than the contribution from solar radiation. On the nightside, however, precipitating protons are a significant heat source compared to the solar radiation.
Future modeling work would be to study solar wind He++ precipitation patterns on Mars. The analysis also implies that new high spatial resolution 3D hybrid simulations with a self-consistent ionosphere should be performed in the future in order to resolve accurately the region near the Martian exobase. The inclusion of the crustal magnetic anomalies would be also of interest because of the possible screening of the Martian atmosphere by the mini-magnetospheres.
References
Acuña, M. H. et al., Magnetic field and plasma observations at Mars: Preliminary Results of the Mars Global Surveyor Mission, Science, 279, 5357,1676–1680, 1998.
Acuña, M. H. et al., Global distribution of crustal magnetization discovered by the Mars Global Surveyor MAG/ER experiment, Science, 284, 5415,790–793,1999.
Brain, D. A. et al., The magnetic field draping direction at Mars from April 1999 through August 2004, Icarus, 182(2), 464–473, 2006.
Brecht, S. H., Magnetic asymmetries of unmagnetized planets, Geophys. Res. Lett., 17(9), 1243–1246, 1990.
Brecht, S. H., Solar wind proton deposition into the Martian atmosphere, J. Geophys. Res., 102(A6), 11,287–11,294, 1997.
Brecht, S. H. and S. A. Ledvina, Control of ion loss from Mars during solar minimum, Earth Planets Space, 64, this issue, 165–178, 2012.
Chaufray, J. Y. et al., Observation of the hydrogen corona with SPICAM on Mars Express, Icarus, 195(2), 598–613, 2008.
Cravens, T. E. et al., Electron Impact Ionization in the vicinity of Comets, J. Geophys. Res., 92(A7), 7341–7353, 1987.
Diéval, C. et al., A case study of proton precipitation at Mars: Mars Express observations and hybrid simulation, J. Geophys. Res., 2011 (submitted).
Dubinin, E. et al., Mass-loading asymmetry in upstream region near Mars, Geophys. Res. Lett., 21(24), 2769–2772, 1994.
Dubinin, E. et al., Hydrogen exosphere at Mars: Pick-up protons and their acceleration at the bow shock, Geophys. Res. Lett., 33, L22103, 2006.
Dubinin, E. et al., Asymmetry of plasma fluxes at Mars. ASPERA-3 observations and hybrid simulations, Planet. Space Sci., 56, 832–835, 2008.
Fedorov, A. et al., Structure of the martian wake, Icarus, 182(2), 329–326, 2006.
Fulle, M. et al., Discovery of the atomic iron tail of comet McNaught using the heliospheric imager on STEREO, Astrophys. J., 661, 93–96, 2007.
Jin, H. et al., Effects of charge exchange and electron impact ionization on the formation of the magnetic pileup boundary at Mars, J. Geophys. Res., 111, A05306, 2006.
Kallio, E. and S. Barabash, On the elastic and inelastic collisions between the precipitating hydrogen atoms and Martian atmospheric neutrals, J. Geophys. Res., 105(A11), 24,973–24,996, 2001.
Kallio, E. and P. Janhunen, Atmospheric effects of proton precipitation in the Martian atmosphere and its connection to the Mars-solar wind interaction, J. Geophys. Res., 106(A4), 5617–5634, 2001
Kallio, E. and P. Janhunen, Modelling the solar wind interaction with Mercury by a quasineutral hybrid model, Ann. Geophys., 21(11), 2133–2145, 2003.
Kallio, E. et al., Charge exchange near Mars: The solar wind absorption and energetic neutral atom production, J. Geophys. Res., 102(A10), 22,183–22,197, 1997.
Kallio, E. et al., On the properties of O+ and
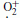 ions in a hybrid model and in Mars Express IMA/ASPERA-3 data: A case study, Planet. Space Sci., 56, 1204–1213, 2008.
ions in a hybrid model and in Mars Express IMA/ASPERA-3 data: A case study, Planet. Space Sci., 56, 1204–1213, 2008.Kallio, E. et al., Oxygen ion escape at Mars in a hybrid model: High energy and low energy ions, Icarus, 206, 152–163, 2010.
Lundin, R. et al., Solar wind-induced atmospheric erosion at Mars: First results from ASPERA-3 on Mars Express, Science, 305, 5692, 1933–1936, 2004.
Lundin, R. et al., On the relation between plasma escape and the Martian crustal magnetic field, Geophys. Res. Lett., 38, L02102, 2011.
Ma, Y. et al., Three-dimensional, multispecies, high spatial resolution MHD studies of the solar wind interaction with Mars, J. Geophys. Res., 109, A07211, 2004.
Nagy, A. F. et al., The plasma environment of Mars, Space Sci. Rev., 111, 33–114, 2004.
Nilsson, H. et al., Heavy ion escape from Mars, influence from solar wind conditions and crustal magnetic fields, Icarus, 215(2), 475–484, 2011.
Shematovich, V. I. et al., Protons and hydrogen atoms transport in the Martian upper atmosphere with an induced magnetic field, J. Geophys. Res., 116, A11320, 2011.
Stenberg, G. et al., Observational evidence of alpha particle capture at Mars, Geophys. Res. Lett., 38, L09101, 2011.
Zhang, M. H. G., J. G. Luhmann, and A. J. Kliore, An Observational Study of the Nightside Ionospheres of Mars and Venus with Radio Occultation Methods, J. Geophys. Res., 95(A10), 17095–17102, 1990.
Acknowledgments
C. D. and G. S. are supported by the National Graduate School of Space Technology of the Luleå Technical University. Figure 2 is made using the VisIt open source visualization tool. The authors thank Arnaud Valeille, University of Michigan, for providing the hot hydrogen and hot oxygen profiles used in the hybrid model.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Diéval, C., Kallio, E., Stenberg, G. et al. Hybrid simulations of proton precipitation patterns onto the upper atmosphere of Mars. Earth Planet Sp 64, 121–134 (2012). https://doi.org/10.5047/eps.2011.08.015
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.5047/eps.2011.08.015







 ions in a hybrid model and in Mars Express IMA/ASPERA-3 data: A case study, Planet. Space Sci., 56, 1204–1213, 2008.
ions in a hybrid model and in Mars Express IMA/ASPERA-3 data: A case study, Planet. Space Sci., 56, 1204–1213, 2008.