Tsunami: Science, Technology, and Disaster Mitigation
- Article
- Open access
- Published:
Three-dimensional numerical analysis to predict behavior of driftage carried by tsunami
Earth, Planets and Space volume 64, Article number: 14 (2012)
Abstract
This study aims to develop a three-dimensional (3D) numerical analysis code for the prediction of driftage behavior during a tsunami. The main features of this code are as follows: (1) it can simulate the six degree-of-freedom motion of driftage in a 3D flow field; (2) it can consider the interaction between fluid flow and driftage motion; and (3) it can compute the impact of the collision with a wall based on the Lagrangian equation of impulsive motion. In this code, we assume that the fluid pressure and viscosity cause driftage motion and that driftage motion affects fluid flow through deformation of the boundary between the fluid and itself. The code was applied to a hydraulic experiment carried out by subjecting a wooden body to an abrupt flow of water. The obtained numerical solution of driftage motion agreed well with the experimental result. It is concluded that our code can be used to successfully predict the behavior of driftage carried by a tsunami.
1. Introduction
During the Indian Ocean Tsunami in 2004, rubble, cars, etc., drifted toward coastal areas with the receding waves and destroyed buildings and structures. Rubble from destroyed structures was also adrift, causing increased damage. To reduce such damage, it is essential to predict the behavior and collision force of tsunami driftage. Ushijima et al. (2006) and Kawasaki et al. (2006) proposed methods for the three-dimensional (3D) simulation of tsunami driftage. These methods can simulate driftage behavior accurately by treating the driftage as a fluid; however, they also have to simulate the air flow. In this study, we have developed a numerical method that does not require the simulation of the air flow to predict the driftage behavior across a wide coastal area. Yoneyama et al. (2002) performed a numerical analysis of the locally high run-up caused by the 1993 Hokkaido-Nansei-Oki seismic tsunami. The wave height calculated by them agreed well with the actual wave height. We believe that the driftage behavior can be simulated with a high degree of accuracy by appending a driftage simulation function to their fluid analysis code. We had developed a vertical two-dimensional (2D) analysis code based on this method, and had verified its validity (Nagashima et al., 2008). In this study, we developed a new 3D numerical analysis code that can simulate the six degree-of-freedom motion of driftage. We verified the validity of this code by comparing the obtained results with a numerical result and with the results of hydraulics model test.
2. Numerical Analysis Method
Our method treats the driftage as a rigid body that is set in motion by the gravitational and fluid forces; these forces are determined by a fluid analysis (see Fig. 1). Meanwhile, the fluid analysis treats the driftage as a moving boundary that is expressed in terms of the porosity ratio of the computational cell γv and the aperture ratio of the cell surface γa (see Fig. 2).
The movement of driftage causes a change in the porosity ratio and in the aperture ratio of the computational cell. This change affects the fluid flow; this effect can be expressed by the following continuity equation.
2.1 Basic equations for fluid flow
The basic equations of fluid flow are shown below.
Continuity equation

Motion equation (i = 1, 2, 3)

Advection equation of fluid

where u
i
is the component of flow velocity; g
i
, the component of the external force per unit volume (vector representation is g); p, the pressure; ρ, the density of the fluid; ν, the dynamic viscosity; F, the fluid-filling ratio of the void in a cell; −, the Reynolds averaging quantity; and, the fluctuation in the Reynolds averaging quantity. We also used the following k-ε model of turbulent flow to calculate Reynolds stress 



where  is the turbulent energy
is the turbulent energy  dissipation, and δ
ij
is the Kronecker delta. The constant numbers in Eqs. (4), (5), and (6) are σ
k
= 1.0, σε = 1.3, Cε1 = 1.45, Cε2 = 1.92, Cμ = 0.09.
dissipation, and δ
ij
is the Kronecker delta. The constant numbers in Eqs. (4), (5), and (6) are σ
k
= 1.0, σε = 1.3, Cε1 = 1.45, Cε2 = 1.92, Cμ = 0.09.
Our method is based on the SIMPLE method (Patankar and Spalding, 1972); we use discretized equations (Eqs. (1), (2), and (3)) on the Cartesian coordinate system to represent fluid flow. The definition points of the flow velocity and the others were at the center of the boundary phase between the cells and at the centers of the cells, respectively. The discretizations of time, advective term, and others yielded the forward difference, third-order upwind difference, and centered difference, respectively. Moreover, we discretized Eq. (3) using the volume of fluid (VOF) method (Hirt et al., 1981). We also devised a few countermeasures to conserve fluid volume (Yoneyama, 1998).
2.2 Basic equations of driftage motion
The driftage motion calculation is based on rigid motion analysis. In addition to the Cartesian coordinate system used in fluid analysis, an inertia principal-axis coordinate system is used for the analysis of driftage motion. The coordinate system moves with a driftage, and its origin is the centroid (gravity center) of the driftage (see Fig. 3).
In this paper, the driftage contained in each calculation cell is called a “segment,” and the surface of the driftage contained in each cell is called the “segment surface” (see Fig. 4). The basic equations of rigid motion are as follows.
Equation of motion of the driftage centroid

Equation of rotational motion about the driftage centroid

where m is the mass of the driftage, v
g
is the driftage centroid velocity vector, and  and
and  are the vectors of the fluid pressure and viscous force, respectively, acting on the segment surface. ω is an angular velocity vector on the inertia principal-axis coordinate system.
are the vectors of the fluid pressure and viscous force, respectively, acting on the segment surface. ω is an angular velocity vector on the inertia principal-axis coordinate system.  is an inertia tensor that consists of the inertia moment of driftage.
is an inertia tensor that consists of the inertia moment of driftage.  is the position vector of the centroid of a segment surface on the inertia principal-axis coordinate system.
is the position vector of the centroid of a segment surface on the inertia principal-axis coordinate system.
2.3 Algorithm of fluid force that acts on driftage
2.3.1 Pressure Fpr
As shown in Eq. (9), the pressure that acts on a “segment surface” Ppr is estimated by using the cell pressure Pc (see Fig. 5).

where h is the vertical interval between the centroid of a segment surface and the cell center; rs, the position vector of the centroid of a segment; and rc, the position vector of the cell center. In this estimation, a hydrostatic pressure is assumed to be acting between the centroid of a segment surface and the cell center. Therefore, the fluid pressure acting on a segment surface is expressed by

where S is the area of a segment surface and n, the normal vector of the surface. In case of a cell including a water surface, a centroid and an area of the submerged part of the segment surface are used for estimation (see Fig. 5(b)).
2.3.2 Viscous force Fvis
If U(r) is a velocity vector at a position r, then the component of the velocity vector parallel to a segment surface Up is expressed as follows.

If rs is the centroid of a segment surface, then the shear stress on the surface, τ(rs) is expressed as follows (see Fig. 6).

where μ is the viscosity coefficient of the fluid and η, a coordinate axis with origin rs that is directed along a normal vector n.
Thus, the viscosity force acting on a segment surface Fvis can be expressed as

2.4 Calculation related to collision
When the collision is predicted to occur before the following calculation step (between t and (t + Δt)), the motion of the driftage is calculated as follows.
-
i)
Calculate the velocity of the driftage centroid, v g , and the angular velocity of the inertia principal-axis, ω, using the basic equations of driftage motion.
-
ii)
Calculate the time of the collision occurrence (t + Δtcol) and the position vector of the collision point on the inertia principal-axis rcol using v g and ω.
-
iii)
Calculate the velocity of the driftage centroid
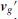 and the angular velocity of the inertia principal-axis ω′ immediately after collision using the following equations.
and the angular velocity of the inertia principal-axis ω′ immediately after collision using the following equations. ((14))
((14)) ((15))
((15))where ncol is the normal vector of the collision surface (wall, bed etc); and J, the impulse force, given by the following expression.
 ((16))
((16))where e is the reflection coefficient.
-
iv)
Calculate the position of driftage centroid X g and rotation angle of inertia principal-axis θ g at time of t + Δt by using v g , ω,
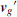 and ω′.
and ω′.
In this procedure, Fpr and Fvis is not changed before and after the collision. Equations (14) and (15) are derived from the Lagrangian equation of impulsive motion, which was applied the Newton’s hypothesis.
2.5 Calculation procedure
The calculation procedure is as follows:
-
i)
Read the input data.
-
ii)
Set the boundary condition for flow velocity
 and pressure pn at time t.
and pressure pn at time t. -
iii)
Calculate the turbulence energy kn+1, the turbulent energy dissipation εn+1, and the eddy viscosity
 at time t + Δt.
at time t + Δt. -
iv)
Calculate the flow velocity
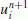 at time t + Δt using the discretized form of Eq. (2).
at time t + Δt using the discretized form of Eq. (2). -
v)
Calculate the position and rotation angles of the driftage,
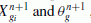 and
and  , respectively, at time t + Δt using the discretized forms of Eqs. (8) and (9).
, respectively, at time t + Δt using the discretized forms of Eqs. (8) and (9). -
vi)
Calculate the void ratio and aperture ratio, γvn+1 and
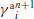 , respectively, at time t + Δt.
, respectively, at time t + Δt. -
vii)
Calculate the error in the continuity equation D using the discretized form of Eq. (1). If D exceeds the limit Dmax, then correct the pressure pn+1 on the basis of the solution of the pressure error equation and return to step iv). If not, then proceed to step viii).
-
viii)
Calculate the fluid-filling ratio Fn+1 at time t + Δt.
-
ix)
If it is time to stop, then stop the calculation. If not, increase the time and return to step ii).
3. Application and Discussion
3.1 Case 1: driftage in sea
Ikeno et al. (2001) conducted a hydraulic experiment to determine the collision force of an object with a simple geometry drifted by a tsunami; they proposed a formula to determine the approximate collision force. Their experimental apparatus is shown in Fig. 7. The model scale is 1/100. The gate was quickly opened, water from the reservoir flowed toward the wall, and the object drifted. The driftage in this case is a wooden object and its specific gravity is 0.5. One side of the experimental flume is made of clear glass and the motion of the driftage was recorded from the glass side using a high-resolution video camera.
The experimental conditions for calculations using our method were as follows: Water levels were H1 = 40 cm, H2 = 5 cm. The driftage was a cylinder with a diameter of 8 cm and a height of 20 cm. The initial position of the centroid of this object was Y = 8.95 m. The computation conditions are as follows: The grid spacing is 6.5 cm along the direction across the flow, 6 cm along the flow direction, and 3 cm in the vertical direction. The computational time interval Δt is 1.0 × 10−3 s, The maximum permissible error of the continuity equation Dmax is 1.0 × 10−5, fluid density ρ is 1.0 × 103 kg/m3, kinematic viscosity ν is 1.0 × 10−6 m2/s, density of the driftage ρ d is 0.5 × 103 kg/m3, and the reflection coefficient between the driftage and vertical wall e is 0.5. For computational purposes, the cylindrical driftage was modeled as an octagonal pillar with cross-sectional area and volume equal to that of the actual cylinder (driftage).
Figure 8 shows the results of a comparison between the vertical 2D trajectory of the driftage obtained by the computation and that obtained in the experiment. In this figure, the trajectories of the centroid of the front-end face (land side) and the rear-end face (sea side) of the driftage are compared. The circles denote the location of the centroid of the front-and rear-end face of the driftage after every 0.5 s from the start of its motion. “×” indicates the location where the driftage collided with the vertical wall.
Figure 9 shows examples of the simulation results. The time shown in this figure indicates the time elapsed since the start of the experiment.
As shown in Fig. 8, the computed driftage trajectory, time variation of the position, and point of collision are in good agreement with the corresponding experimental results. Therefore, we concluded that our code can successfully predict the behavior of driftage in the sea.
3.2 Case 2: driftage on land
Ikeno and Tanaka (2003) conducted another hydraulic experiment to determine the behavior of driftage on land. The experimental apparatus is shown in Fig. 10. This apparatus is the same as that in Case 1 with the exception of a 10-cm-high ground segment in the front of the vertical wall. The driftage is a square pillar with side 4.5 cm and height 89 cm. The initial position of the driftage centroid is Y = 9.02 m. The other experimental and computational conditions are the same as those in Case 1. In the analysis, the bottom surface of the driftage is raised by 0.005 m from the surface of the ground segment. This was done so that the water flowing through the 0.005-m gap would exert an upward force on the driftage.
Figure 11 shows the results of a comparison between the vertical 2D trajectory of the driftage obtained by the computation and that obtained in the experiment. In this figure, the trajectories of the driftage centroid are compared. The circles and the “×” carry the same meaning as in Fig. 8.
Figure 12 shows examples of the simulation results.
As shown in Fig. 11, the computed trajectory elevation of the driftage between the initial position and the vertical wall was higher than the experimental result. Therefore, the collisions that occurred at low elevations in the experiment did not show in the computation results. This difference might be caused by the initial gap between the driftage and the ground surface. In future works, it is necessary to understand the mechanism of initial movement and to find a suitable initial condition.
However, in general, the computed drifting behavior agrees well with the experimental results despite the initial movement problem. Therefore, we concluded that our code can successfully predict the behavior of driftage on land.
4. Conclusion
The results of our research are summarized as follows:
-
A numerical analysis code has been developed to predict the behavior of driftage carried by a tsunami. The main features of the code are as follows.
-
It can simulate driftage motion with six degrees-of-freedom in a 3D flow field.
-
It can consider the interaction between a fluid flow and a driftage motion.
-
It can determine the impact of the collision of driftage with a wall on the basis of the La-grangian equation of impulsive motion.
-
-
To verify the validity of the code, the obtained computational results were compared with the results of two hydraulic experiments. The behavior of driftage and the time variation of its position as calculated using our code were in good agreement with the experimental results.
-
It can be concluded that our code can be used to successfully predict the behavior of driftage carried by a tsunami.
In the future, the code will be applied to various drifting motions and it will be improved such that it can be used to simultaneously predict the behavior of several drifting objects. Furthermore, a method will be developed to determine the collision force; this was not discussed in this paper.
References
Hirt, C. W. and B. D. Nichols, Volume of fluid (VOF) method for the dynamics of free boundaries, J. Comput. Phys., 39, 201–225, 1981.
Ikeno, M. and H. Tanaka, Experimental study on impulse force of drift body and tsunami running up to land, Ann. J. Coast. Eng., JSCE, 50, 721–725, 2003.
Ikeno, M., N. Mori, and H. Tanaka, Experimental study on drift behavior and its impulse force by tsunami, Ann. J. Coast. Eng., JSCE, 48, 846–850, 2001.
Kawasaki, K., S. Yamaguchi, M. Hakamada, N. Mizutani, and S. Miya-jima, Wave pressure acting on drifting body after collision with bore, Ann. J. Coast. Eng., JSCE,53, 786–790, 2006.
Nagashima, H., N. Yoneyama, and K. Toda, Numerical analysys of the drift behavior in tsunami run-up using the FAVOR method, Adv. Hydro-Sci. Eng., VIII, CD-ROM, 2008.
Patankar, S. V. and D. B. Spalding, A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flow, J. Heat Mass Transfer, 15, 1787, 1972
Ushijima, S., S. Yamada, S. Fujioka, and I. Nezu, Prediction method (3D MICS) for transportation of solid bodies in 3D free-surface flows, J. Hydrau. Coast. Environ. Eng., JSCE, 810/II-74, 79–89, 2006.
Yoneyama, N., Development of free surface hydraulic analysis code (FRESH), Nagare (Jpn. Soc. Fluid Mech.), 17(3), 1998.
Yoneyama, N., M. Matsuyama, and H. Tanaka, Numerical analysis for locally high runup of 1993 Hokkaido Nansei-oki Seismic Tsunami, J. Hydrau. Coast. Environ. Eng., JSCE, 705/II-59, 139–150, 2002.
Acknowledgments
The authors are indebted to Dr. Masaaki Ikeno, Central Research Institute of Electric Power Industry, Japan, for kindly supplying his experiment data.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yoneyama, N., Nagashima, H. & Toda, K. Three-dimensional numerical analysis to predict behavior of driftage carried by tsunami. Earth Planet Sp 64, 14 (2012). https://doi.org/10.5047/eps.2011.11.010
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.5047/eps.2011.11.010






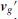 and the angular velocity of the inertia principal-axis ω′ immediately after collision using the following equations.
and the angular velocity of the inertia principal-axis ω′ immediately after collision using the following equations.


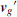 and ω′.
and ω′. and pressure pn at time t.
and pressure pn at time t. at time t + Δt.
at time t + Δt.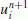 at time t + Δt using the discretized form of
at time t + Δt using the discretized form of 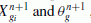 and
and  , respectively, at time t + Δt using the discretized forms of
, respectively, at time t + Δt using the discretized forms of 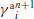 , respectively, at time t + Δt.
, respectively, at time t + Δt.




