Physical Processes in Non-Uniform Finite Magnetospheric Systems—50 Years of Tamao's Resonant Mode Coupling Theory
- Article
- Open access
- Published:
Ballooning modes and their stability in a near-Earth plasma
Earth, Planets and Space volume 65, pages 463–471 (2013)
Abstract
As a possible trigger of the substorm onset, the ballooning instability has been often suggested. The ballooning disturbances in a finite-pressure plasma immersed into a curved magnetic field are described with the system of coupled equations for the Alfven and slow magnetosonic modes. The spectral properties of ballooning disturbances and instabilities can be characterized by the local dispersion equation. The basic system of equations can be reduced to the dispersion equation for the small-scale in transverse direction disturbances. From this relationship the dispersion, instability threshold, and stop-bands of the Alfvenic and slow magnetosonic modes have been determined. The field-aligned structure of unstable mode is described with the solution of the eigenvalue problem in the Voigt model. We have also analyzed in a cylindrical geometry an eigenvalue problem for the stability of ballooning disturbances with a finite scale along the plasma inhomogeneity. The account of a finite scale in the radial direction raises the instability threshold as compared with that in the WKB approximation.
1. Introduction: Ballooning Instability of Near-Earth Plasma as a Substorm Trigger
The key dilemma of the physics of terrestrial space environment is related to the identification of the substorm onset mechanism: does it occur in the magnetotail owing to magnetic field reconnection, or in a closed field line region as a result of some still unidentified instability? Tamao and his colleagues were the first who suggested that the ballooning instability could be a possible trigger of the substorm explosive phase (Miura et al., 1989; Ohtani and Tamao, 1993). This instability can be imagined as a distortion of radial gradient of hot plasma pressure by locally outward expansion and inward intrusion due to the azimuthally oscillating mode. The analysis of satellite observational data led Roux et al. (1991) to the suggestion that an instability driven by the plasma pressure gradient is responsible for the field-aligned current generation during the substorm onset. Later the idea about the ballooning instability as an onset trigger has been extensively elaborated (e.g., Lee and Wolf, 1992; Cheng et al., 1994; Liu, 1997; Cheremnykh et al., 2004; Agapitov et al., 2007).
In realistic magnetosphere the mechanisms of the ballooning instability in the near-Earth tail and reconnection in a distant magnetotail are probably coupled. The computer experiments with advanced models of the magnetosphere showed that the substorm onset was caused by violation of the balance between the thermal plasma pressure and Ampere’s force, resulting into the plasma expulsion and field lines extension into the magnetotail (Raeder et al., 2010). As a result, decrease of the magnetic component normal to the current sheet destabilized the tearing instability and stimulated the magnetic field reconnection. Thus, though the main substorm power is released via the reconnection, the substorm onset trigger could be the ballooning instability. To understand better the physical mechanisms of the processes involved in the substorm development, the results of the numerical modeling and in-situ satellite observations are to be compared with simplified, but more explicit, theoretical models.
A theoretical approach to the study of the ballooning instability is based on a complicated system of coupled equations for the poloidal Alfven waves and slow magnetosonic (SMS) modes in a finite-pressure plasma, immersed in a curved magnetic field B (e.g., Southwood and Saunders, 1985; Walker, 1987; Hameiri et al., 1991; Klimushkin and Mager, 2008). Favorable conditions for the instability growth emerge at a steep plasma pressure drop held by curved field lines. Such a condition may occur before sub-storm onset on strongly extended field lines.
The easiest way to comprehend qualitatively the basic features of the unstable modes and instability condition is the analysis of the local dispersion equation. The dispersion equation, obtained using a local analysis of this system, is widely used for geophysical applications both for the examination of plasma stability, and for the description of spectral properties of ULF wave phenomena in the nighside auroral magnetosphere (Safargaleev and Maltsev, 1986; Ohtani and Tamao, 1993; Liu, 1997; Golovchanskaya and Kullen, 2005).
However, the exact form of the dispersion equation used by different authors happens to be somewhat different, and the obtained results differ, too. Thus, it is necessary to check the derivation of the dispersion equation from basic MHD equations and the transfer to various limiting cases, which will be done in this paper.
In order to evaluate a field-aligned scale of ballooning-unstable modes, we consider the eigenvalue problem in the self-consistent analytical model of magnetic field and finite-pressure plasma (Voigt, 1986). However, an estimation of the instability criterion in the local approximation for a particular magnetic shell has necessarily a qualitative character because of the WKB approximation in the radial direction used during the solution of relevant equations. In a realistic situation an unstable mode near a steep gradient of the plasma pressure has a finite scale across the magnetic shells, which cannot be described by the WKB approximation.
Therefore, in this paper we consider the global stability with the use of very simplified magnetic field geometry (a cylindrical field with constant curvature field lines), which has enabled us to obtain some analytical results.
2. MHD Plasma Equilibrium and Linearized Dynamic Equations
We consider a finite pressure plasma confined by a 2D curved magnetic field B(x, z) with a local curvature radius R c . We introduce a local orthogonal basis, organized by the B field geometry: e3 = B/B is in field-aligned direction, and e1 = e2 × e3 corresponds to the radial direction across magnetic shell. Along e2 = e y (Y-axis) the system is homogeneous.
Derivatives along the basis vectors are ∇
n
= e
n
∙ ∇. The inhomogeneities of plasma and magnetic field are characterized by 3 local parameters: κP = P−1∇1P, κ
B
= B−1∇1B, and the field line curvature  . The local equilibrium condition of plasma with scalar pressure P(x, z) can be written via these κ -parameters as follows:
. The local equilibrium condition of plasma with scalar pressure P(x, z) can be written via these κ -parameters as follows:

Under equilibrium the plasma pressure P(x, z) is constant along a field line.
For the harmonic disturbance ~exp(− iωt) the linearized MHD equations are

whereρis unperturbed density, ξ is the plasma displacement, and b and p are disturbed magnetic field and pressure. We exclude b from the first equation (2) and proceed from the variables ξ3, p to the new variables: u = ∇ ∙ ξ and the normalized disturbance of the total pressure q = μ0B−2(p + Bb3/μ0). The variable u characterizes the plasma compression and is related to its field-aligned displacement by the relationship  . As a result we get the linearized MHD equations, which coincide with equations for 2D case from (Cheng, 2002), but for different variables:
. As a result we get the linearized MHD equations, which coincide with equations for 2D case from (Cheng, 2002), but for different variables:

Here the following notations have been introduced: V
a
= B(μ0ρ)−1/2 is the Alfven velocity,  is the Alfven wave number, V
s
= (γP/ρ)1/2 is the sound velocity,
is the Alfven wave number, V
s
= (γP/ρ)1/2 is the sound velocity,  is the sound wave number,
is the sound wave number,  is the “cusp ” velocity, and
is the “cusp ” velocity, and  . We introduce also the following operators:
. We introduce also the following operators:
-
Alfven poloidal
 ,
, -
Alfven toroidal
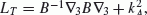 ,
, -
magnetosonic
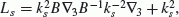 and
and -
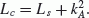 .
.
The typical time scale of the substorm explosive phase (~1−2 min) is much less than the Alfven transit time along the extended field lines from the magnetotail to the ionosphere (~10 min). Therefore, influence of the ionospheric boundaries on the ballooning mode properties can be neglected, assuming that the growing disturbances are localized in the near-equatorial region of the nightside magne-tosphere. The influence of the ionospheric boundary conditions on the ballooning modes was considered in many papers (e.g., Cheremnykh and Parnowski, 2006).
2.1 Asymptotic theory of transverse small-scale disturbances
For small-scale in the transverse (across B) direction disturbances the linearized MHD equations of a finite pressure plasma can be simplified and reduced to a system of ordinary differential equations for coupled Alfven and SMS modes. General approach to the 3D case with account for the gravity and plasma rotation effects was outlined by Hameiri et al. (1991). Our analysis of 2D configuration is given in another form.
The asymptotic solution for the harmonics (ξ, u,q) ∝ exp(ik1x1 + ik2x2) of the system (2) for large transverse wave numbers  may be searched in the form
may be searched in the form

(similar for u and q) where ε is a small parameter.
From the system of order ε−1 it follows that the azimuthal displacement component ξ2 and the perturbation of the total pressure q are small values of the order of  . Further, in the zero-th order of ε the closed system of equations occurs
. Further, in the zero-th order of ε the closed system of equations occurs

The system (4) is a special case of the system (71) from (Hameiri et al., 1991). It can be re-written in the following form (Klimushkin, 1998)

The relationship between different disturbance components is given by formulas  , and
, and  . Both Alfven and SMS modes convey the field-aligned current
. Both Alfven and SMS modes convey the field-aligned current  . For the ballooning disturbances (k2 ≪ k1) the component b2 → 0, hence
. For the ballooning disturbances (k2 ≪ k1) the component b2 → 0, hence  .
.
2.2 Local dispersion equation
The spectral properties of the ballooning modes can be qualitatively understood with the use of local dispersion equation. Let us suppose that a disturbance has a small scale not in the transverse direction only, but also along the field line. In the geometrical optics approximation ȝ exp (ikǁx3) all operators turn into numerical factors  , and
, and  . The linear system of differential equations (4) now becomes an algebraic system. The dispersion equation is obtained by setting the determinant of this system to zero, namely
. The linear system of differential equations (4) now becomes an algebraic system. The dispersion equation is obtained by setting the determinant of this system to zero, namely

where  . Equation (6) is a quadratic in Ω2 with roots
. Equation (6) is a quadratic in Ω2 with roots

where H = βκ c [2γκ c − κ P (2 + γβ)/2] sin2 α. The roots (7) are real for a real kǁ.
The relationship (7) describes two branches: fast (Ω+) mode, which transforms into an Alfven wave as β → 0, and slow (Ω −) mode. Their dispersion curves are shown in Fig. 1. The fast branch  is stable for any kǁ. Only the slow mode
is stable for any kǁ. Only the slow mode  can be unstable under the condition
can be unstable under the condition

This inequality is the generalization for oblique disturbance with k1 ≠ 0 of the ballooning instability condition (Liu, 1997). The maximal value of the growth rate as estimated from the dispersion relation (7) is

If κb ≪ κc, then, taking into account (1), (9) is reduced to  .
.
Dispersion curves  (solid line) and
(solid line) and  (dashed line) for dimensionless frequency Ω = ω/(κ
c
V
a
sinα) depending on parameter β (shown near curves): (left-hand panel) at Λ = −1 (stable plasma); (right-hand panel) Λ = 1. At Λ = 1 the maximal cut-off frequency Ω+(0) is reached at β = 0.991. In the region
(dashed line) for dimensionless frequency Ω = ω/(κ
c
V
a
sinα) depending on parameter β (shown near curves): (left-hand panel) at Λ = −1 (stable plasma); (right-hand panel) Λ = 1. At Λ = 1 the maximal cut-off frequency Ω+(0) is reached at β = 0.991. In the region  the slow branch is unstable.
the slow branch is unstable.
The asymptotic formulas for disturbances with small scales in the field-aligned direction are obtained from (7) assuming kǁ ≫ κ c sinα:


where  . Here the parameter Λ = κ
P
/κ
c
has been introduced. Its absolute value ǀ Λ ǀ = R
c
/a is the ratio between the curvature radius R
c
and the plasma inhomogeneity scale
. Here the parameter Λ = κ
P
/κ
c
has been introduced. Its absolute value ǀ Λ ǀ = R
c
/a is the ratio between the curvature radius R
c
and the plasma inhomogeneity scale  . When Λ < 0 (outward pressure gradient) both branches are stable. When Λ > 0 (inward pressure gradient), the interval
. When Λ < 0 (outward pressure gradient) both branches are stable. When Λ > 0 (inward pressure gradient), the interval  emerges according to (8), where
emerges according to (8), where  , thus the slow mode branch turns out to be unstable.
, thus the slow mode branch turns out to be unstable.
2.3 The possibility of total reflection of poloidal Alfven waves
Analysis of the dispersion equation (7) shows that for real Ω there may occur regions where  (see dispersion curves in Fig. 2). These regions are non-transparent (opaque) for poloidal Alfven waves. Their occurrence can be qualitatively shown with the use of the formula (7) for
(see dispersion curves in Fig. 2). These regions are non-transparent (opaque) for poloidal Alfven waves. Their occurrence can be qualitatively shown with the use of the formula (7) for  . Wave meets the turning points
. Wave meets the turning points  when its frequency Ω matches the cut-off frequency
when its frequency Ω matches the cut-off frequency

The exact formula (12) differs somewhat from that in (Mager et al., 2009) obtained with the use of asymptotic relationship (11). In a disturbed nightside magne-tosphere with tailward extended field lines, the curvature ǀκ
c
(x3)ǀ increases sharply equatorward, therefore, in the near-equatorial region the condition  may be fulfilled, and
may be fulfilled, and  becomes negative in this area. This region with high β and locally curved field lines is non-transparent for poloidal Alfven waves.
becomes negative in this area. This region with high β and locally curved field lines is non-transparent for poloidal Alfven waves.
The dispersion curves  (solid lines) and
(solid lines) and  (dashed lines) in the plane of squared parameters Ω2 = [ω/(κ
c
Va sinα)]2, (kǁ/κ
c
sinα)2 depending on parameter Λ = κ
P
/κ
c
(shown near curves) for Λ < 2γ. Other parameters are γ = 5/3, β = 1. The area
(dashed lines) in the plane of squared parameters Ω2 = [ω/(κ
c
Va sinα)]2, (kǁ/κ
c
sinα)2 depending on parameter Λ = κ
P
/κ
c
(shown near curves) for Λ < 2γ. Other parameters are γ = 5/3, β = 1. The area  corresponds to the non-propagation (opaque) region for the fast (Alfven-type) branch.
corresponds to the non-propagation (opaque) region for the fast (Alfven-type) branch.
3. Field-Aligned Structure of Unstable Modes
To characterize the field-aligned structure of unstable ballooning modes beyond the WKB approximation we use the Voigt (1986) model which describes the self-consistent equilibrium of a finite-pressure plasma in the geomagnetic field. This analytical model is based on the assumption of the relationship between the pressure P and vector potential of the magnetic field A = A
y
, namely P = (2μ0)−1K2A2, where the parameter K characterizes the magnetic field distortion by the plasma pressure. Thanks to this assumption the equilibrium Grad-Shafranov equations become linear, and the equation  for the potential A(x, z) can be obtained. The solution of this equation in the band
for the potential A(x, z) can be obtained. The solution of this equation in the band  (which models a magnetosphere engulfed by the solar wind) with the dipole source in the coordinate origin has the form (at
(which models a magnetosphere engulfed by the solar wind) with the dipole source in the coordinate origin has the form (at  )
)

where B
e
is the magnetic field at the Earth’s equator, R
e
is the Earth’s radius,  , and
, and  . The function A(x, z) is constant along a field line. The background magnetic field and its transverse gradient are derived via A(x, z) as follows
. The function A(x, z) is constant along a field line. The background magnetic field and its transverse gradient are derived via A(x, z) as follows

Using the expressions (14) one can find the parameters which determine the coefficients of the system (4): β = K2A2B−2, κ
P
= 2BA−1, and  . The form of a field line x = x (s), z = z (s) can be determined by the solution of the differential equations
. The form of a field line x = x (s), z = z (s) can be determined by the solution of the differential equations  which depend on the parameter K: when K increases the field line becomes more extended. With the use of (13) and (14) distribution of the basic parameters along a field line can be determined.
which depend on the parameter K: when K increases the field line becomes more extended. With the use of (13) and (14) distribution of the basic parameters along a field line can be determined.
We consider the transverse small-scale asymptotic system (4) for the poloidal disturbance with k2 ≫ k1. The spectrum of eigenfrequencies comprises the infinite number of stable discrete modes  and an unstable mode with
and an unstable mode with  . The field-aligned structure of the unstable eigenmode at L = 10R
e
has been numerically modeled (Fig. 3). In a high-pressure plasma, βmax ≃ 20, both the magnetic field compression bǁ and transversal plasma displacement ξ1 of the unstable disturbance are localized in vicinity of a field line top. The field-aligned scale of disturbance is about ±1.5R
e
, hence it is localized within the same region where β is high.
. The field-aligned structure of the unstable eigenmode at L = 10R
e
has been numerically modeled (Fig. 3). In a high-pressure plasma, βmax ≃ 20, both the magnetic field compression bǁ and transversal plasma displacement ξ1 of the unstable disturbance are localized in vicinity of a field line top. The field-aligned scale of disturbance is about ±1.5R
e
, hence it is localized within the same region where β is high.
The field-aligned structure (s—the coordinate along the field line measured from the magnetospheric equator s = 0) of unstable mode in the Voigt model under  . The parameters of the model used are x
b
= 5R
E
, z
b
= 3R
E
. The plasma density is assumed to be constant. Upper panel: the field-aligned distribution of parameter β; middle panel: transverse plasma displacement ξ1, and the characteristics of plasma compression u = ∇ ∙ ξ; bottom panel: magnetic field compression bǁ = b3, and the transversal component of magnetic disturbance b⊥ = b1.
. The parameters of the model used are x
b
= 5R
E
, z
b
= 3R
E
. The plasma density is assumed to be constant. Upper panel: the field-aligned distribution of parameter β; middle panel: transverse plasma displacement ξ1, and the characteristics of plasma compression u = ∇ ∙ ξ; bottom panel: magnetic field compression bǁ = b3, and the transversal component of magnetic disturbance b⊥ = b1.
4. Global MHD Stability of the Ballooning Mode in a Cylindrical Geometry
In contrast to the local analysis of the plasma stability in Section 2, here we perform a global analysis, but in the framework of a simple cylindrical model. The cylinder axis is along coordinate y, which corresponds to the azimuthal direction in the magnetosphere. Magnetic field lines are circles with radius r. This simplified model possesses all the typical features necessary for occurrence of the ballooning instability: field line curvature and a plasma pressure gradient. This model can be considered as an element of a more general configuration, specifically in the region of strongly disturbed field lines. The structure of the disturbance harmonic along a field line is assumed to be ∝ exp(− iωt + ivθ), where the parameter v determines the field-aligned wave number as kǁ = v/r.
From the general MHD equations (2) we obtain a system of ordinary differential equations for the perturbed radial component of the displacement ξ = ξ r and the normalized disturbance of the total pressure q:

The coefficients of this system are as follows:

Here the operators have been reduced to the algebraic factors  , and
, and  . Our consideration is not limited by the transversely small-scale limit k⊥→ ∞, so the system (15) describes coupled Alfven, fast magnetosonic (FMS), and SMS modes for arbitrary transverse scales.
. Our consideration is not limited by the transversely small-scale limit k⊥→ ∞, so the system (15) describes coupled Alfven, fast magnetosonic (FMS), and SMS modes for arbitrary transverse scales.
We suppose that plasma pressure is described by the modeling radial profile

where a is the typical scale of inhomogeinity, and r0 is the position of the plasma gradient maximum. The pressure drops to some background level far from the plasma gradient: P → P∞ at r → ∞, whereas the density distribution ρ(r) is homogeneous. The parameter β0 = β(r0) varies within the limits 0–1, and characterizes the global “temperature ” of a plasma; its increase results in the raising of the β(r) profile. For values of β0 → 1, the local values of the actual β(r) parameter may be rather high: maxβ(r) ~ 10 if β0 = 0.95 and a/r0 = 0.1.
5. The Boundary Problem for the Growth Rate Determination
We consider the boundary problem for the system (15) in a semi-infinite interval with the boundary condition ξ(R
e
) = 0 and the requirement of bounded ξ (r ) as r → ∞. The system parameters for which instability is possible are determined by the occurrence of discrete eigenvalues  . The values
. The values  , when this problem has a solution, determine the growth rates Γ = Im ω > 0 for the corresponding eigenfunctions.
, when this problem has a solution, determine the growth rates Γ = Im ω > 0 for the corresponding eigenfunctions.
We reduce the system (15) to one 2-nd order equation in a normal form. Excluding q from (15) and using the standard change of variables technique one arrives at

The function I (r) plays the role of the squared local radial wave number  , and is determined by a cumbersome combination of the coefficients (16) and their derivatives. A bounded solution may occur only when I (r) > 0 in a sufficiently long interval. An example of the I (r ; ω2) dependence, when discrete spectrum can emerge, is shown in Fig. 4 (top panel). When the absolute magnitudes of negative ω2 are large, the function I (r ) < 0 for all r > 0, hence a bounded solution does not exist. When ω2 grows and approaches zero, an interval emerges where I (r) > 0, therefore the occurrence of discrete eigenvalues becomes possible. The eigenvalues
, and is determined by a cumbersome combination of the coefficients (16) and their derivatives. A bounded solution may occur only when I (r) > 0 in a sufficiently long interval. An example of the I (r ; ω2) dependence, when discrete spectrum can emerge, is shown in Fig. 4 (top panel). When the absolute magnitudes of negative ω2 are large, the function I (r ) < 0 for all r > 0, hence a bounded solution does not exist. When ω2 grows and approaches zero, an interval emerges where I (r) > 0, therefore the occurrence of discrete eigenvalues becomes possible. The eigenvalues  of the boundary problem and the corresponding eigenfunctions have been calculated numerically. An example, when the spectrum comprises 3 eigenvalues, is presented in Fig. 4 (bottom panel).
of the boundary problem and the corresponding eigenfunctions have been calculated numerically. An example, when the spectrum comprises 3 eigenvalues, is presented in Fig. 4 (bottom panel).
Figure 5 (left-hand panel) shows the dependence of the spectrum on the parameter β0. In the limit β0 → 0 the spectrum  evidently does not exist. For v ≠ 0 there is a threshold value of
evidently does not exist. For v ≠ 0 there is a threshold value of  (v) for the plasma stability. For a higher β0 the growth rate further increases.
(v) for the plasma stability. For a higher β0 the growth rate further increases.
The dependence of eigenvalues  on the azimuthal wave number k
y
for a given v = 0.5 is shown in Fig. 5 (right-hand panel). The model used enables us to consider the instability pattern for an arbitrary k
y
. This consideration shows that the instability is possible even for azimuthally large-scale modes,
on the azimuthal wave number k
y
for a given v = 0.5 is shown in Fig. 5 (right-hand panel). The model used enables us to consider the instability pattern for an arbitrary k
y
. This consideration shows that the instability is possible even for azimuthally large-scale modes,  . The growth rate increases rapidly with the increase of k
y
and at
. The growth rate increases rapidly with the increase of k
y
and at  gradually reaches the saturation.
gradually reaches the saturation.
In the local WKB approximation for the cylindrical geometry  the instability threshold (8) in the limiting case k
y
→ ∞ is as follows
the instability threshold (8) in the limiting case k
y
→ ∞ is as follows

The comparison of the instability thresholds in the WKB approximation (19) and obtained by numerical solution is given in Fig. 6. The solid line shows the extreme value of the destabilizing term -βκ P r for different azimuthal scales k y a. The disturbances with v2 < max(-βκ P r) are unstable. The dashed lines show the critical value of v, above which the discrete spectrum is absent. Thus, for any v the threshold by parameter β0 for disturbances of finite-scale along the radius is higher than the threshold predicted by the local theory (19).
6. Discussion
The description of the ballooning instability by (Ohtani and Tamao, 1993) owing to a mathematical error (Liu, 1997) resulted in an incorrect conclusion about the possible instability of both wave branches. Miura et al. (1989) predicted a possible instability of Alfven-type disturbances with the growth rate  . However, their assumption u = 0 (or ξǁ = 0) used for isolating the Alfven mode turns out to be inconsistent with the second equation from the basic system (4). Analysis of the dispersion relationship (6) in the poloidal limit k1 = 0 shows that no branch
. However, their assumption u = 0 (or ξǁ = 0) used for isolating the Alfven mode turns out to be inconsistent with the second equation from the basic system (4). Analysis of the dispersion relationship (6) in the poloidal limit k1 = 0 shows that no branch  can intersect the line
can intersect the line  . The relation
. The relation  from (Miura et al., 1989) contradicts this condition. Thus, the Alfven-type branch is always stable,
from (Miura et al., 1989) contradicts this condition. Thus, the Alfven-type branch is always stable,  .
.
The favorable conditions for the balloon instability growth may occur under strongly extended into the magne-totail field line before the substorm onset (Zhu et al., 2009). At the linear stage of the ballooning instability a disturbance grows exponentially, though drift effects may produce oscillatory growth and azimuthal drift with the velocity of about the Larmor drift velocity (Miura et al., 1989).
Using the energy principle, the ideal MHD stability of ballooning-type perturbations for a “hard ” ionospheric boundary condition was considered by Lee and Wolf (1992). For self-consistent analytical model of the magnetosphere, they found that if a magnetotail configuration was stable to interchange, it was also stable against symmetric ballooning. We suppose that in a realistic magnetosphere the ballooning modes are to be localized near the mag-netospheric equator, where the parameter β and curvature rapidly increase. Indeed, the field-aligned structure of unstable ballooning modes described within the Voigt model is strongly localized in the vicinity of the top of field lines.
In a radial direction the growing disturbances are localized in the region of pressure gradient, whereas the scale of fundamental mode is about the pressure inhomogeneity scale. The radial fundamental mode has a lowest threshold in respect to the parameter β0, whereas the threshold value β0 is higher than it follows from the local criterion. The az-imuthally small-scale disturbances with k y a ≫ 1 have the growth rate of the fundamental mode Γ ≃ (V A /a)ImΩ ≃ 0.03 c−1 for V a = 500 km/s and a = 0.8R e . This value agrees with the estimate following from the local approximation (9). The characteristic growth time of the instability ~ Γ−1 ≃ 30 s is about the typical time scale of the substorm explosive phase.
The cylindrical model has enabled us to consider the stability for an arbitrary k
y
, which showed that even an azimu-tally large-scale mode, k
y
a ≪ 1, can be destabilized. Such mode, named KY0 mode, indeed was found unexpectedly during numerical modeling (Raeder et al., 2010). The instability growth rate increases with the increase of k
y
in the range  , and reaches the saturation for the azimuthal wave numbers
, and reaches the saturation for the azimuthal wave numbers  . This behavior fits the results of the numerical modeling (Zhu et al., 2004).
. This behavior fits the results of the numerical modeling (Zhu et al., 2004).
For the considered model the source of free energy for the ballooning instability is the excess of the hot plasma pressure in the radial direction. However, our model does not take into account few factors which might be significant for the instability development: pressure anisotropy (Cheng and Qian, 1994), drift effect (Miura et al., 1989), kinetic effects (Klimushkin and Mager, 2008), and the azimuthal pressure gradient related to a background field-aligned current (Ivanov et al., 1992; Golovchanskaya and Maltsev, 2003). The ballooning instability can be excited nonlin-early by an external trigger (Hurricane et al., 1999). For such “MHD detonation ” the magnetospheric plasma must be near the threshold level, determined by the linear theory of instability, and an external trigger must have a magnitude sufficient to transfer the system into the nonlinear explosive growth phase.
7. Conclusion
We have discussed the dispersion relationship, instability threshold, and stop-bands for the Alfvenic-type and SMS-type modes which can be used for space applications. The Alfven-type branch is always stable. For poloidal Alfven waves with frequencies less than the cut-off frequency (12) a non-transparent region may occur, which makes the wave propagation along the whole field line impossible.
In the region with a steep drop of the finite pressure plasma, held by curved magnetic field lines, an instability of the SMS-type mode may become feasible. When the ballooning instability threshold is exceeded the hot plasma expands locally outward. The disturbance grows aperiodi-cally, though drift effects (neglected here) may produce an oscillatory growth. Unstable disturbance is strongly localized in the region of a field line with high β and strong curvature.
In the radial direction unstable disturbances are non-propagating modes localized near the plasma gradient. The fundamental mode has the lowest threshold, whereas the threshold per se is somewhat higher than what follows from the local criterion.
References
Agapitov, A. V., O. K. Cheremnykh, and A. S. Parnowski, Ballooning perturbations in the inner magnetosphere of the Earth: Spectrum, stability and eigenmode analysis, Adv. Space Res., 41, 1682, 2007.
Cheng, C. Z., MHD field line resonances and global modes in three-dimensional magnetic fields, J. Geophys. Res., doi:10.1029/2002JA009470, 2002.
Cheng, C. Z. and Q. Qian, Theory of ballooning-mirror instabilities for anisotropic pressure plasmas in the magnetosphere, Geophys. Res. Lett., 99, 11193, 1994.
Cheng, C. Z., Q. Qian, K. Takahashi, and A. T. Y. Lui, Ballooning-mirror instability and internally driven Pc 4–5 wave events, J. Geomag. Geo-electr., 46, 997, 1994.
Cheremnykh, O. K. and A. S. Parnowski, Influence of ionospheric conductivity on the ballooning modes in the inner magnetosphere of the Earth, Adv. Space Res., 37, 599–603, 2006.
Cheremnykh, O. K., A. S. Parnowski, and O. S. Burdo, Ballooning modes in the inner magnetosphere of the Earth, Planet. Space Sci., 55, 1217–1229, 2004.
Golovchanskaya, I. V. and A. Kullen, Ballooning-type instabilities and waves in the Earth’s magnetosphere (review), Proc. of 28-th Annual Seminar. Apatity, 93–99, 2005.
Golovchanskaya, I. V. and Yu. P. Maltsev, Interchange instability in the presence of the field-aligned current: Application to the auroral arc formation, J. Geophys. Res., 108, 1106, doi:10.1029/2002JA009505, 2003.
Hameiri, E., P. Laurence, and M. Mond, The ballooning instability in space plasmas, J. Geophys. Res., 96, 1513–1526, 1991.
Hurricane, O. A., B. H. Fong, S. C. Cowley et al., Substorm detonation, J. Geophys. Res., 104, 10221–10231, 1999.
Ivanov, V. N., O. A. Pokhotelov, F. Z. Feiygin, A. Roux, S. Perrot, and D. Lecau, Balloon instability in the Earh’s magnetosphere under non-constant pressure and finite β, Geomagn. Aeron., 32, 68–74, 1992.
Klimushkin, D. Yu., Theory of azimuthally small-scale hydromagnetic waves in the axisymmetric magnetosphere with finite plasma pressure, Ann. Geophys., 16, 303–321, 1998.
Klimushkin, D. Yu. and P. N. Mager, On the spatial structure and dispersion of slow magnetosonic modes coupled with Alfven modes in planetary magnetospheres due to field line curvature, Planet. Space Sci., 56, 1273, 2008.
Lee, D.-Y and R. A. Wolf, Is the Earth’s magnetotail balloon unstable?, J. Geophys. Res., 97, 19251–19257, doi:10.1029/92JA00875, 1992.
Liu, W. W., Physics of the explosive growth phase: Ballooning instability revisited,J. Geophys. Res., 102, 4927–4931, 1997.
Mager, P. N., D. Yu. Klimushkin, V. A. Pilipenko, and S. Schafer, Field-aligned structure of poloidal Alfven waves in a finite pressure plasma, Ann. Geophys., 27, 3875–3882, 2009.
Miura, A., S. Ohtani, and T. Tamao, Ballooning instability and structure of diamagnetic waves in a model magnetosphere, J. Geophys. Res., 94, 15231, 1989.
Ohtani, S. and T. Tamao, Does the ballooning instability trigger substorms in the near-Earth magnetotail?, J. Geophys. Res., 98, 19369–19379, 1993.
Raeder, J., P. Zhu, Y Ge, and G. Siscoe, Open Geospace General Circulation Model simulation of a substorm: Axial tail instability and ballooning mode preceding substorm onset, J. Geophys. Res., 115, A00I16, doi:10.1029/2010JA015876, 2010.
Roux, A., S. Perraut, P. Robert et al., Plasma sheet instability related to the westward travelling surge, J. Geophys. Res., 96, 17697–17714, doi:10.1029/91JA01106, 1991.
Safargaleev, V. V. and Yu. P. Maltsev, Internal gravity waves in the plas-masheet, Geomagn. Aeron., 26, 220–223, 1986.
Southwood, D. J. and M. A. Saunders, Curvature coupling of slow and Alfven MHD waves in a magnetotail field configuration, Planet. Space Sci., 33, 127–134, 1985.
Voigt, G.-H., Magnetospheric equilibrium configurations and slow adia-batic convection, in Solar Wind-Magnetosphere Coupling, edited by Y. Kamide and J. A. Slavin, 233–273, Terra Sci., Tokyo, 1986.
Walker, A. D. M., Theory of magnetospheric standing hydromagnetic waves with large azimuthal wave number, 1. Coupled magnetosonic and Alfven waves, J. Geophys. Res., 92, 10039–10045, 1987.
Zhu, P., A. Bhattacharjee, and Z. W. Ma, Finite ky ballooning instability in the near-Earth magnetotail, J. Geophys. Res., 109, A11211, 2004.
Zhu, P., J. Raeder, K. Germaschewski, and C. C. Hegna, Initiation of ballooning instability in the near-Earth plasma sheet prior to the 23 March 2007 THEMIS substorm expansion onset, Ann. Geophys., 27, 1129–1138, 2009.
Acknowledgments
This study is supported by grant 13-05-90436 from RFBR and Program 22 of Russian Academy of Sciences. We appreciate constructive suggestions of both reviewers.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mazur, N.G., Fedorov, E.N. & Pilipenko, V.A. Ballooning modes and their stability in a near-Earth plasma. Earth Planet Sp 65, 463–471 (2013). https://doi.org/10.5047/eps.2012.07.006
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.5047/eps.2012.07.006
 ,
,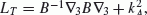 ,
,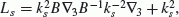 and
and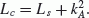 .
.



 (normalized by a) for various
(normalized by a) for various  (upper panel). The discrete spectrum comprises 3 eigenvalues
(upper panel). The discrete spectrum comprises 3 eigenvalues  , and
, and  . Their eigenfunctions ξ
n
(r) are shown in the bottom panel. The parameters used are β0 = 0.95, P∞/P0 = 1, a/r0 = 1/6, v = 0.5, and k
y
a = 2.
. Their eigenfunctions ξ
n
(r) are shown in the bottom panel. The parameters used are β0 = 0.95, P∞/P0 = 1, a/r0 = 1/6, v = 0.5, and k
y
a = 2.
