- Article
- Open access
- Published:
Explicitly computing geodetic coordinates from Cartesian coordinates
Earth, Planets and Space volume 65, pages 291–298 (2013)
Abstract
This paper presents a new form of quartic equation based on Lagrange’s extremum law and a Groebner basis under the constraint that the geodetic height is the shortest distance between a given point and the reference ellipsoid. A very explicit and concise formulae of the quartic equation by Ferrari’s line is found, which avoids the need of a good starting guess for iterative methods. A new explicit algorithm is then proposed to compute geodetic coordinates from Cartesian coordinates. The convergence region of the algorithm is investigated and the corresponding correct solution is given. Lastly, the algorithm is validated with numerical experiments.
1. Introduction
The transformation between Cartesian coordinates and geodetic coordinates is a basic problem frequently encountered in geodesy and astronomy, e.g., in GPS positioning. Computing Cartesian coordinates from geodetic coordinates is a very easy task, but the inverse transformation poses a difficulty. For the latter, numerous solutions have been proposed, which can be classified into two categories. One category is an iterative solution. Bowring (1976) derived a trigonometric equation which was solved by the Newton algorithm with a single iteration. Fukushima (1999) solved a modified Borkowski’s quartic equation by the Newton method, and, later, Fukushima (2006) developed a new and faster iterative procedure using Halley’s method. Jones (2002) found a new solution with the Newton method in the reduced latitude. Pollard (2002) presented two vector methods which do not involve quartic equations, and Feltens (2009) has also presented a vector method. The other category are closed form solutions, which maybe more straightforward and efficient; however, they are relatively rare until recently. Paul (1973) proposed a closed form solution based on the well-known theory for solutions of biquadratic equations (Burnside and Panton, 1904). Borkowski (1989) proposed two accurate closed solutions, of which one is approximate and the other is exact. Vermeille (2002) proposed a closed-form algebraic method, which is well known and is used the most. Vermeille (2004) improved the formulae of Vermeille (2002) to extend the validity domain. Zhang et al. (2005), using the method of extrema with constraints and generalized La-grange’s multipliers obtained a four new equations, and presented an alternative algebraic algorithm. Gonzalez-Vega and Polo-Blanco (2009) have used symbolic tools to characterize the Vermeille and Borkowski approaches. Feath-erstone and Claessens (2008) have reviewed the state of the art of closed-form transformations between geodetic and ellipsoidal coordinates.
This paper presents a new form of quartic equation with Lagrange’s extremum law and a Groebner basis technique, and seeks a very explicit and concise formulae of the quartic equation by Ferrari’s line. A new algorithm to compute geodetic coordinates from Cartesian coordinates is then presented, and the convergence region of the algorithm is investigated. Lastly, the algorithm is validated through numerical experiments.
2. Description of the Presented Algorithm
2.1 Brief review of a Groebner basis
A Groebner basis for ideals in a polynomial ring was developed by B. Buchberger in 1965. It is a method of establishing the standard basis of a nonlinear polynomial system as follows. In the polynomial ring formed by the original nonlinear polynomial system, after the proper sort of the polynomial variables, seek the S-polynomial (subtraction polynomial) of the polynomial pairs from the polynomial ring, and then carry out polynomial reduction and elimination. Finally, a standard basis is generated which is completely equal with the original system, and which neither increases, nor decreases, the roots.
If the Groebner basis of the polynomial system F is GB, for all of the polynomial pairs (f i , f j ) ∈ F, their S-polynomial S(f i , f j ) is divisible by GB. Based on the above nature of a Groebner basis, the Buchberger algorithm is put forward to construct the Groebner basis of the polynomial system efficiently as follows:
-
Step 1: Let G := F.
-
Step 2: Construct set B of polynomial pairs from G. B = {(f i , f j ) ǀ f i , f j ∈ G, i ≠ j}.
-
Step 3: If B is a null set, go to Step 10.
-
Step 4: Select an element of B, (f i , f j ), and exclude it from B, i.e., let B = B − {(f i , f j )}.
-
Step 5: Compute the S-polynomial s = S(f i , f j ).
-
Step 6: Compute the remainder following the division of s by the G, denoted by
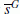 .
. -
Step 7: If
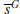 , go to Step 3.
, go to Step 3. -
Step 8: Add
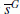 into set
into set 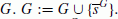 .
. -
Step 9: Update
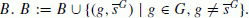 . Turn to Step 4.
. Turn to Step 4. -
Step 10: Output the reduced Groebner basis GB according to G.
2.2 Problem formulation based on Lagrange’s constraint and a Groebner basis
The relationship between Cartesian and geodetic coordinates (B, L, h) (B, L are the latitude and longitude, respectively) at any point P can be constructed according to the following formulae (see Fig. 1):

where  , and a, b, e denote the semi-major axis, the semi-minor axis, and the eccentricity of the reference ellipsoid, respectively. As we know, the geodetic height h is the distance from the reference ellipsoid to P in a direction normal to the ellipsoid, so it denotes the shortest distance from P to the surface of the ellipsoid. Suppose that p with Cartesian coordinates (x, y, z) is a point at the surface of the ellipsoid, thus
, and a, b, e denote the semi-major axis, the semi-minor axis, and the eccentricity of the reference ellipsoid, respectively. As we know, the geodetic height h is the distance from the reference ellipsoid to P in a direction normal to the ellipsoid, so it denotes the shortest distance from P to the surface of the ellipsoid. Suppose that p with Cartesian coordinates (x, y, z) is a point at the surface of the ellipsoid, thus

with a constraint

According to Lagrange’s extremum law, we obtain the Lagrange equation as

where λ is the Lagrange multiplier. By taking the partial derivative of Eq. (4) to x, y, z, and λ, respectively, wefurther obtain

In order to solve the nonlinear polynomial equation, the Buchberger algorithm to obtain the Groebner basis of the nonlinear polynomial system of Eq. (5), which has the identical solution to Eq. (5). The obtained Groebner basis includes 16 polynomial elements. If the lexicographic order (x > y > z > λ) is chosen, the corresponding 16 elements are as listed in the Appendix. We note that the first polynomial in the Appendix is a univariate polynomial of degree four in λ, thus we can solve the polynomial equation as follows to obtain λ.

where

2.3 The presented algorithm
According to Ferrari’s lines (see Shmakov, 2011, and a little revision is made), the four roots of Eq. (6) can be obtained as

where

Note that either sign of the square root will do for the expression of ξ.
Substituting λ i (i = 1, 2, 3,4) into Eq. (5), we obtain four solutions p i (x i , y i , z i ) of pointp (x, y, z) as

Next, we compute the geodetic coordinates (B, L, h), as follows:
-
(1)
Computation of B
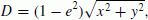 (10)
(10)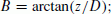 (11)
(11)however, for the case D = 0, i.e. B = ±90°, the Eq. (11) is undefined. It can be computed as follows by the tangent of the half value.
 (12)
(12)thus
 (13)
(13)Note this formula is fit for the case that B = ±90°; namely, the region of the poles.
-
(2)
Computation of LBy means of Eq. (1), the following expression is obtained,
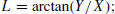 (14)
(14)however when X = 0, i.e. L = ±90°, Eq. (14) has no meaning. In the same manner as the computation of B, we can compute L as follows.
 (15)
(15)considering its applicability of Eq. (15), we obtain
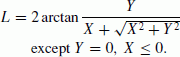 (16)
(16)Note it is suitable for any case except Y = 0, X ≤ 0, i.e. L = ±180°.
-
(3)
Computation of h
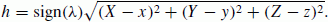 (17)
(17)
2.4 Convergence region of the presented algorithm
Obviously, there are some regions in which a point can have many geodetic coordinates. If P is the center of Earth, i.e. X = 0, Y = 0, Z = 0, the presented algorithm is invalid, and the geodetic coordinates of P may be B = 0°, L ∈ [−180°, 180°], h = −a, or B = ±90°, L ∈ [−180°, 180°], h = −b. If P is in the region of the polar axis, i.e. X = 0, Y = 0, Z > 0 or X = 0, Y = 0, Z < 0, its geodetic coordinates are B = 90°, L ∈ [−180°, 180°], h = −b, or B = −90°, L ∈ [−180°, 180°], h = −b. It is proved below that the formula of B and h of the presented algorithm is suitable in the region of the polar axis.
Except for the special regions above, a point in any region, including the equatorial plane, should have its unique geodetic coordinates. However, one can note that the algorithm may yield four, at most, solutions of the point p (x, y, z), and this can be explained as follows. The evolute of the reference ellipsoid (see Fig. 1), which is the envelope of all the normal lines through the ellipse surface, is the boundary of judging the number of the solutions of point p. In the common regions expect the center, the polar axis, and the equatorial plane of the Earth, if P is outside the evolute (its mathematical equation is (W/ka)2/3 + (Z/kb)2/3 = 1, where ka = (a2 − b2)/a = ae2, kb = (a2 − b2)/b = be′2, and e′ is the second eccentricity of the reference ellipsoid), it will have two solutions of p; if P is on the evolute, it will have three solutions of p; if P is inside the evolute, it will have four solutions of p. This is illustrated in Fig. 4. Only one correct solution of p is to be selected. And it is necessary to turn to numerical analysis for help.
As is known, a polynomial equation in one variable with real coefficients has pairs of conjugate complex number roots, suppose that it has complex number roots. And as a real world matter, the point p (x, y, z) must have at least one solution. So there are two, or four, real number solutions of point p. This agrees with the above geometrical analysis. Next, the correct solution of p will be given for different regions.
-
(1)
Region near the center of the Earth It is indicated by numerous computations that in the region near the center of the Earth (approximately having the sphere of radius
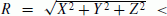 from the center of the Earth) the solution of the equation is singular. That is to say the algorithm is invalid in this region.
from the center of the Earth) the solution of the equation is singular. That is to say the algorithm is invalid in this region. -
(2)
Region of the polar axis of the Earth The real number solution of p is shown in Fig. 2, and the solution is summarized in Table 1.
Table 1. Solution of p in the region of the polar axis. -
(3)
Region of the equatorial plane of the Earth The real number solution of p is shown in Fig. 3, and the solution is summarized in Table 2.
Table 2. Solution of p in the region of the equatorial plane. -
(4)
Region except near the center, the polar axis, and the equatorial plane of the Earth The real number solution of p is shown in Fig. 4, and the solution is summarized in Table 3.
Table 3. Solution of p in the region except near the center, the polar axis, and the equatorial plane of the Earth.
Whereas Figs. 2, 3, and 4, are depicted for the case that B ∈ [0°, 90°], L ∈ [0°, 180°], the conclusion of Tables 1, 2, and 3, can apply for the globe, i.e. B ∈ [−90°, 90°], L ∈ [−180°, 180°].
3. Numerical Experiments and Discussion
3.1 Experiments for the surface, and outer space, regions of the Earth
The surface, and outer space, regions of the Earth are the most common regions that geodesy considers. For thousands of grid points evenly distributed throughout the entire region with B ranging from 0° to 90° and h from 1 to 108 m, I first compute their Cartesian coordinates, then recover the geodetic coordinates from the Cartesian coordinates applying both the algorithm presented here and that presented by Vermeille (2004). The computation was carried out with the ellipsoid parameter of GRS80. The statistics of errors (ΔB, Δh are the errors in latitude and height, respectively) are listed in Table 4. From Table 4, we can see that the algorithm presented here is slightly better than that presented by Vermeille for ΔB, but slightly worse for Δh; however, they are comparable overall and meet the need of any precise geodesy. Figures 5 and 6 depict the distributions of ΔB and Δh, through which the comparison can be made intuitively.
3.2 Experiments for the inner space region of the Earth
In some special cases, we also need to compute the geodetic coordinates from the Cartesian coordinates for the region below the surface of the reference ellipsoid. The experiments adopt the same reference ellipsoid and simulative computation method as described in Subsection 3.1.
-
(1)
Region of the polar axis of the EarthThe simulated computation indicates that the error ΔB is always zero, and the errors Δh are correlated with the distance S between the point P and the center of the Earth, which is shown in Table 5. It is seen from Table 5 that the error decreases dramatically with an increase of S. If an accuracy of one centimeter (common geodetic demand) is required, S must be more than 100 km.
Table 5. The magnitude of error Δh corresponding to different values of S along the polar axis. -
(2)
Region of the equatorial plane of the EarthThe simulated computation indicates that the error ΔB is always zero, and the errors Δh are correlated to the distance between the point P and the center of the Earth, which is shown in Table 6. It is seen from Table 6 that with an increase of S inside the evolute, the error decreases dramatically to the 10-meter level, and then increases dramatically to +∞; with an increase of S outside the evolute, the error again decreases dramatically. If an accuracy of one centimeter (common geodetic demand) is required, S must be more than 200 km.
Table 6. The magnitude of error Δh corresponding to different values of S in the equatorial plane. -
(3)
Region except near the center, polar axis and equatorial plane of the EarthThe simulated computation indicates that the errors ΔB and Δh are correlated with the distance between the point P and the center of the Earth, which are shown in Tables 7 and 8, taking the case that B = 11°, L = 45° for example. It is seen from Tables 7 and 8 that the errors ΔB and Δh decrease dramatically with an increase of S.
Table 7. The magnitude of error ΔB corresponding to different values of S in the region except near the center, the polar axis and the equatorial plane. Table 8. The magnitude of error Δh corresponding to different values of S in the region except near the center, the polar axis and the equatorial plane. Because the algorithm presented by Vermeille (2004) is invalid when the distance between the point P and the center of the Earth is less than 43 km, I do not compare the two algorithms for this region, and the result is comparable with other regions.
4. Conclusion
A new explicit algorithm for computing geodetic coordinates from Cartesian coordinates is presented. Numerical experiments indicate that it is correct for any point except the region near the center of the Earth, and give a good transformation accuracy for different regions, including the surface, outer, and inner space, of the Earth. The results show that the presented algorithm is comparable to the algorithm of Vermeille (2004).
References
Borkowski, K. M., Accurate algorithms to transform geocentric to geodetic coordinates, Bull. Geod., 63, 52–54, 1989.
Bowring, B. R., Transformation from spatial to geodetic coordinates, Surv. Rev., 23, 323–327, 1976.
Burnside, W. S. and A. W. Panton, Theory of Equations, Dublin Univ. Press Series, p. 121–125, 1904.
Featherstone, W. E. and S. J. Claessens, Closed-form transformation between geodetic and ellipsoidal coordinates, Stud. Geophys. Geod., 52, 1–18, 2008.
Feltens, J., Vector method to compute the Cartesian (X, Y, Z) to geodetic (φ, λ, h) transformation on a triaxial ellipsoid, J. Geod., 83, 129–137, 2009.
Fukushima, T., Fast transform from geocentric to geodetic coordinates, J. Geod., 73, 603–610, 1999.
Fukushima, T., Transformation from Cartesian to geodetic coordinates accelerated by Halley’s method, J. Geod., 79, 689–693, 2006.
Gonzalez-Vega, L. and I. Polo-Blanco, A symbolic analysis of Vermeille and Borkowski polynomials for transforming 3D Cartesian to geodetic coordinates, J. Geod., 83, 1071–1081, 2009.
Jones, G. C., New solutions for the geodetic coordinate transformation, J. Geod., 76, 437–446, 2002.
Paul, M. K., A note on computation of geodetic coordinates from geocentric (Cartesian) coordinates, Bull. Geod., 108(2), 135–139, 1973.
Pollard, J., Iterative vector methods for computing geodetic latitude and height from rectangular coordinates, J. Geod., 76, 36–40, 2002.
Shmakov, S. L., A universal method of solving quartic equations, Int. J. Pure Appl. Math., 71, 251–259, 2011.
Vermeille, H., Direct transformation from geocentric coordinates to geodetic coordinates, J. Geod., 76, 451–454, 2002.
Vermeille, H., Computing geodetic coordinates from geocentric coordinates, J. Geod., 78, 94–95, 2004.
Zhang, C. D., H. T. Hsu, X. P. Wu, S. S. Li, Q. B. Wang, H. Z. Chai, and L. Du, An alternative algorithm to transform Cartesian to geodetic coordinates, J. Geod., 79, 413–420, 2005.
Acknowledgments
The work of this paper is supported by the National Natural Science Foundation of China (Grant No. 41104009), Open Research Fund Program of the Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, China (Grant No. 11-01-04), and the Open Foundation of the Key Laboratory of Precise Engineering and Industry Surveying, National Administration of Surveying, Mapping and Geoinformation of China (Grant No. PF2011-4). The author is grateful to the support and good working atmosphere provided by his research team in China Three Gorges University. The author also thanks Professor Kiyoshi Yomogida of Hokkaido University, Japan, Associate Professor Shinichi Miyazaki of Kyoto University, Japan, and two anonymous reviewers for valuable comments and suggestions, which enhanced the quality of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Copyright ©c The Society of Geomagnetism and Earth, Planetary and Space Sciences (SGEPSS); The Seismological Society of Japan; The Volcanological Society of Japan; The Geodetic Society of Japan; The Japanese Society for Planetary Sciences; TERRAPUB.
Appendix.
Appendix.

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zeng, H. Explicitly computing geodetic coordinates from Cartesian coordinates. Earth Planet Sp 65, 291–298 (2013). https://doi.org/10.5047/eps.2012.09.009
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.5047/eps.2012.09.009
 .
.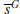 , go to Step 3.
, go to Step 3.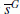 into set
into set 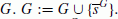 .
.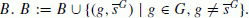 . Turn to Step 4.
. Turn to Step 4.


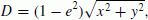
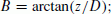


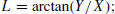

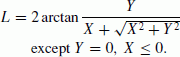
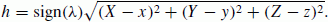

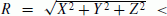 from the center of the Earth) the solution of the equation is singular. That is to say the algorithm is invalid in this region.
from the center of the Earth) the solution of the equation is singular. That is to say the algorithm is invalid in this region.
