- Article
- Open access
- Published:
Toward a better representation of the secular variation. Case study: The European network of geomagnetic observatories
Earth, Planets and Space volume 65, pages 767–779 (2013)
Abstract
In the present paper we discuss a few issues regarding the secular variation (SV) and secular acceleration (SA) of the geomagnetic field that have consequences on mapping them at regional scales. Data from the European network of geomagnetic observatories have been analyzed from the perspective offered by existing long time series of annual means. The existence of high-frequency ingredients in the temporal change of the main field has been taken into account too. The importance of eliminating, from observatory and main field model data, prior to any discussion on secular variation, the signal related to external variations is demonstrated. Its consequences for SV analysis and/or mapping, including the jerk concept, are shown. Also, the importance of the geographical scale at which the SV is represented is discussed. To that aim, we used gufm1, IGRF and CM4 models for the main field from which the residual external signature was eliminated. The contribution of high-frequency ingredients to the map pattern is revealed. The results of the paper set additional observational constraints to the main field and geodynamo modeling.
1. Introduction
An inspection of sources that contribute the observed geomagnetic field at Earth’s surface reveals the well known three main contributors, namely the core field (also called the main field), the lithospheric field and the external field (Mandea and Purucker, 2005; Olsen et al., 2007). They are produced, respectively, by a dynamo process in the outer core, by the magnetized rocks above the Curie temperature in the lithosphere and by the interaction of solar radiative and particle output with the ionosphere and magnetosphere. We also need to take into account that both the external and the core time-varying fields induce a time-varying response field in the solid Earth by two different mechanisms. One is magnetic induction in the magnetic material of the lithosphere above the Curie temperature (generally the crust) and the other is electromagnetic induction in the crust and mantle conductive structures. Correctly evaluating the secular variation (SV), i.e. of the time change underwent by the core field, is of great importance to geodynamo modeling. It requires eliminating from data the contribution of the lithospheric field, as well as of the external field and of its induced response in the Earth.
The temporal change of the observed field at a given point on the Earth’s surface, generally expressed by its first time derivative, would be described by six terms, three of internal origin and three of external origin. Schematically we have

where “obs” stands for “observed”, “mi” stands for “magnetic induction”, and “emi” for “electromagnetic induction”. The superscript indicates the inducing field and the subscript indicates the process by which the contribution to the respective variation term is created. The terms in square brackets indicate the region of the solid Earth affected by the sources and processes corresponding to the superscripts and, respectively, to the subscripts. The remanent magnetization of rocks plays, of course, no role in the field time variation.
If the external contribution, direct and induced, is properly accounted for, the time variation of the observed field would contain only information on the core field, in a nonlinear fashion that depends on magnetic properties of rocks above the Curie temperature and of the electric properties of the crust and mantle structures.
Unless the two induced internal terms are independently known, only the change of the entire internal field can be obtained from data. The temporal evolution of this field would be similar to the temporal evolution of the core field, except the amplitude. This is because the induced crust field would vary in phase with the core field, on one hand, and we do not expect large phase differences of the electromag-netically induced field in the crust and mantle conductive structures with respect to the inducing core field, on the other hand. However, as regards the amplitude of the temporal change, one could expect differences, that might be significant, between the core and the entire internal field. Nevertheless, a quantitative approach would be needed to assess this aspect. Recent progress has been made in this direction by Thébault et al. (2009) and Hulot et al. (2009). Both papers make use of the vertically integrated susceptibility (VIS) values calculated by Hemant and Maus (2005) in a global network of 0.25° × 0.25° resolution. The former estimated the secular variation produced by the crust by calculating the response of the VIS model to variations of the core field as described by the CM4 model (Sabaka et al., 2004). The latter concludes, based on the spatial spectrum of the field changes in terms of spherical harmonic analysis, that up to a critical degree of 22–24 the observed changes in the field of internal origin are likely to be the secular variation of the core field, but, beyond that degree, the signal produced by the time-varying lithospheric field is bound to dominate and conceal the time-varying core signal.
Individually modeling the three terms related to external variations, attempted in the comprehensive modeling (Sabaka et al., 2002, 2004), is only partially successful up to now, in spite of the significant progress compared to other types of modeling: the solar-cycle-related external term is modeled by means of Dst and F10.7 only, the electromagnetic crust and mantle response is built on a 1D radial distribution of conductivity, deduced (Olsen, 1998) from European data, and the crust response by magnetic induction is completely ignored.
Secular variation studies generally deal with observatory annual means and/or with repeat station data that are reduced to the middle of the measurement year. There is also a tendency to use monthly averages (e.g. Alexandrescu et al., 1995), but, we think, with increased possibilities for external effects to leak into the models. The presence in annual mean data of a solar-cycle-related (SC) signal due to incomplete averaging out of external effects, modulated by the solar activity, has long been recognized (Chapman and Bartels, 1940; Yukutake, 1965; Bhargava and Yacob, 1969; Alldredge, 1975, 1976; Courtillot and Le Mouël, 1976; Alldredge et al., 1979; Yukutake and Cain, 1979; Demetrescu et al., 1988; Verbanac et al., 2007; Wardinski and Holme, 2011). Because at the observing point these effects comprise both the direct and the induced fields, and having in view the frequency difference of the SC variation in comparison to the secular variation, a suitable filter applied to data would eliminate both the external fields and their induced effects. Recent works (Korte and Holme, 2003; Thébault, 2008; Verbanac et al., 2009) use a quite different way to deal with the external signal, modeling the internal field from data by means of a spherical cap harmonic analysis (SCHA). We think that the problem of external effects leaking into the main field model, which we discuss in the present paper in relation with global field models, might be a problem for the SCHA too.
In the present paper we discuss, on data from the European network of geomagnetic observatories, a few issues regarding the secular variation and secular acceleration, with consequences on mapping them at regional scales, from the perspective of the existence of high-frequency ingredients (Demetrescu and Dobrica, 2005, 2013) in the temporal change of the main field. In the next section we present the data and the method we work with, and in Section 3 we describe an empirical approach to obtain information concerning the time variation of the internal field and of its geographical distribution, within the jerk concept applied to SV mapping. In Section 4 we discuss some consequences of having a longer time-perspective on the geomagnetic field evolution, and in Section 5 a discussion on the leakage of the external signals into main field models is made. The SV evolution in the 20th century in Europe, based on global models for the main field is presented in Section 6 from the perspective of the contribution of high-frequency ingredients, at 22- and ~80-year timescale, present in data. The main conclusions of the study are pointed out in the last section of the paper.
2. Data and Method
Annual means of geomagnetic elements H, Z, and D, as given at http://www.geomag.bgs.ac.uk/gifs/annual means. html have been used. The European network of observatories has been chosen to support our demonstrations, as being the densest network available, with high-quality data in a time-span relevant for SV studies. Also, global main field models spanning long-time intervals, namely gufm1 (Jackson et al., 2000), IGRF (Finlay et al., 2010), CM4 (Sabaka et al., 2004) have been used for the same geographical area, to illustrate our viewpoints.
Data temporal distribution for the European network is illustrated in Fig. 1. The largest number of observatories providing data, 34, is reached between 1960 and 2004, making this time interval suitable for mapping the time change of the internal field. The location of the observatories is illustrated in the same figure. Geographical coordinates are given in Table A.1 (Appendix).
The simplest filter to get rid of the SC signal in data would be the running averages with an 11-year window. Experiments with 9 and 12-year windows to encompass the range of the solar cycle length gave similar results. In Fig. 2 we show the H, Z, and D annual means time series (thin black) and the filtered time series (gray), generically denoted by E 11 (E stands for “geomagnetic element”) in the following sections, that represent the internal field, for three observatories with different trends, namely SUA, NGK, and HAD. In the lower panel, the difference E − E 11, i.e. E(11), is shown for the three observatories. The noise in data is mostly kept in the 11-year variation. However, the latter is significant, with amplitudes of 10–20 nT in case of H and Z, and of 2–3 minutes in case of D.
The first step in processing observatory and/or main field model data was to filter out the solar-cycle-related signal present in the annual means at observatories; this signal is leaking in the main field models too, as we show in Section 5. We have chosen the simplest filter—11-year running averages—as presented above. Then we divide our discussion on how to obtain a proper representation of the secular variation in two directions, according to available data: the case of data in a suitable time-span from a relatively dense network of observatories (such as Europe) and the case of main field models that allow retrieving the secular variation in a much longer time interval than observatory data (and, if needed, covering larger areas than possible if using only observatory data). In the first case we used the jerk concept and an empirical approach to describe the field evolution between successive jerks, as described in Section 3. In the second case, our considerations are based on the field evolution in a grid of points of 2° × 2° latitude/longitude over Europe, calculated from global main field models with a long time-span (gufm1, IGRF, CM4). Successively filtering with 11-, 22-, and 80-year running windows of each time series are used to render evident variations at 22- and ~80-year timescales that are present in data (Section 4). In Section 6 we map the contribution of these variations and discuss their contribution to the secular variation.
3. The Jerk Concept Applied to SV Mapping
A geomagnetic jerk represents a sudden V-shaped change in the field first time-derivative, or a step change in the second time-derivative (field acceleration), separating two time intervals of quasi-constant evolution (Courtillot et al., 1978). At the jerk time the field acceleration goes through zero and the field goes through an inflection point. Between jerks the acceleration of the field is constant. Accepted jerks in the 20th century occurred at 1901, 1925, 1969, 1978, 1989, 1999 (e.g. Alexandrescu et al., 1996; Le Huy et al., 1998; Mandea et al., 2000; Sabaka et al., 2004). These moments have been established according to Y orD data, which show jerks clearlyer than other geomagnetic elements. They do not necessarily occur at the same moments in all geomagnetic elements. Within the jerk concept we have to analyze the second time derivative in order to detect jerk moments in the first time derivative and changes in curvature of the field evolution time series. Then we can fit a second order polynomial to each segment of the time series defined according to the curvature sign, in the time interval covered with a homogeneous data set from as many European observatories as possible. This will allow describing the evolution of the internal field and of its time change in a suitable way for map representation, as:

where Eint is the internal part of the geomagnetic element E considered, Δt is the time (in years) elapsed since the beginning of the given segment, and a0, a1, a2 are constants determined by fit.
This way, the secular change of the geomagnetic element E would be:

and the acceleration in the time evolution of the geomagnetic element would be:

So, in a given time interval, for which a0, a1 and a2 were determined for each observatory considered, the time change of the internal field can be mapped for any chosen year. A single map of field acceleration would characterize that time interval. For the time interval 1960–2004 with data from 34 observatories we can define three moments of zero acceleration value in case of H and four in case of D, as seen in Fig. 3 where data for the three observatories selected in Fig. 2 are superimposed: 1969, 1986, and 1999 and, respectively, 1969,1981,1989,1999. They are marked by a vertical bar in the figure. Z data are noisier and a jerk moment is more difficult to define. An attempt to do that is however presented. For the time intervals so defined, applying the above principles results in the maps of Figs. 4–6. They display the geographical distribution of the secular change in two of the defined time intervals for H, Z, and D respectively. The maps compare very well with those derived from SCHA results of Thébault (2008) and Verbanac et al. (2009).
Field acceleration in H (top), Z (middle), and D (bottom) for the three observatories of Fig. 2. Zero values are marked.
The main problem arisen by this kind of mapping concerns the continuity of the SV information at the common epoch of two joining segments of data, because, in reality, as we shall see in the next section, at the two ends of the segment, what we call E11 does not show the sharp V form in its first time derivative, (according to the jerk concept), but rather a smooth evolution over several years.
For times prior to 1960 such maps cannot be produced using observatory data alone, due to the fewer and fewer observatories in operation as one goes back in time. Field models should be used instead. However, the time perspective offered by long time-series of data, discussed in the next section, will introduce new constraints to SV and SA mapping, because, as can be seen in Fig. 7, where secular acceleration of the field for several observatories with longer time-series are plotted, there are time intervals, such as 1919–1970 in H, when the constant acceleration of the field, assumed in the jerk model, is only a crude approximation. Remark also, the high noise level, which will be discussed in the next section.
4. The Time Perspective Offered by Available Long Time-Series of Data
We have recently shown (Demetrescu and Dobrica, 2005, 2013), based on 150–100 year long time series from 24 observatories world-wide and on 400-year long ones from three European sites, that the variations described in the literature as “geomagnetic jerks” are in fact parts of quasi-periodical variations of the main field that we called the “22-year” and the “~80-year” variations, superimposed on what we called the “steady variation”. The impression of change sharpness (1–2 years) given by the first timederivative (first differences) of annual mean values is an effect of the SC variation present in data. Once this external effect eliminated, the time change of the field is much smoother and the transition from decreasing to increasing and from increasing to decreasing values of the secular change takes several years, as can be seen in Fig. 8.
The three columns of the figure refer to H, Z, and D, respectively. The panels in a column illustrate, from top to bottom, the evolution of the internal field (E11) and of its first and second time-derivatives, respectively. Data from HAD are shown, as being the longest time series available (the time series start in 1860). The successive timederivatives of the internal field reveal the existence of higher frequency signals (~5 and 2–3 years), which are completely insignificant in E 11, but are enhanced by the derivative operator and become significant in the time-derivative plots. They are also of external origin, being harmonics of the 11-year cycle, or the expression of the well known behavior of geomagnetic activity with two peaks in a solar cycle, one at maximum and the other in the declining phase (Mayaud, 1980), and/or a result of the asymmetries in the variations of geomagnetic activity (Mursula et al., 1997) and should be regarded as noise. The noise level is increased before 1930, most likely due to well known difficulties in maintaining the base level of recordings.
Several conclusions could be drawn regarding the secular change of the internal field, having at hand the longer time perspective on data plotted in Fig. 8:
-
(1)
the first time-derivative does not show jerks, but display extrema of the combined ~80-year, 22-year, and steady variations; this was first shown on D data by Demetrescu and Dobrica (2005, 2013). Such extrema do not occur at the same time in all geomagnetic elements. For instance, extrema in H occur at 1898, 1919, 1970, 1987, 2000, in Z at 1893, 1919, 1940, 1972, 1982, while in D they occur at 1903, 1927, 1966, 1981, 1990, 2000;
-
(2)
the extrema occur at a different moment than the accepted geomagnetic jerk. That was also noticed by Sabaka et al. (2004) when accounting for the external contribution in data;
-
(3)
the transition between episodes of quasi-constant (in the jerk concept) evolution of the field, i.e. between decreasing and increasing or between increasing and decreasing time-change, is lasting several years in case of declination. In H and Z such transitions last longer (see, for instance, the minimum in
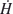 around 1919). This was also noticed by Alexandrescu et al. (1997) in case of declination, and is seen in the CM4 (Sabaka et al., 2004, their figure 8). No conclusions regarding the current jerk concept were advanced by the mentioned authors;
around 1919). This was also noticed by Alexandrescu et al. (1997) in case of declination, and is seen in the CM4 (Sabaka et al., 2004, their figure 8). No conclusions regarding the current jerk concept were advanced by the mentioned authors; -
(4)
as the acceleration is calculated as a time derivative of the secular variation, always zero acceleration values mark extrema in the secular variation evolution. Between two extrema in the first time-derivative and/or zero values of the field acceleration (the second timederivative), the field acceleration shows a variable evolution, with a pulse or a more complex shape. One can no longer consider, for instance, constant field acceleration and a linear variation of the first time-derivative between 1919 and 1970 in H and treat data as in the previous section. A more complex behavior of the acceleration is seen in that time interval, with a maximum around 1950, between the two zero values, in 1919 and 1970. A pulse-like shape of the acceleration is characteristic to the last ~40 years of the plots, dominated by the 22-year variation, while the ~80 year variation controls the field evolution before 1960–1970. The characteristics of these two ingredients of the field where discussed at length by Demetrescu and Dobrica (2005, 2013). This can be seen in Fig. 9, in which the contributions of the 22-year, ~80-year and steady ingredients of the SV and SA, at Hartland geomagnetic observatory, are plotted in case of declination. The upper panel shows the first differences of the annual means (black) and the time-derivatives of the 11-, 22-, and 80-year smoothed data (gray, dashed and dotted, respectively). The middle panel displays the first time-derivative of the 11-, 22- and ~80-year variations (gray, dashed and dotted, respectively), and the lower panel the second time-derivative of the same field ingredients. Arrows mark the accepted jerk moments and vertical lines mark zero values of the acceleration in case of the 22-year and the ~80-year variation. The first and second harmonics of the 11-year variation are enhanced by the derivative operator, most visible in the lower panel. The ~80 year variation in D shows a maximum acceleration at 1918 between the two zero values at ~1903 and 1929, and a specific variation between the zero values at 1929 and 1962, namely a minimum value reached at the beginning of that time interval, followed by a slightly increasing trend to the end of the interval.
-
(5)
jerks are part of a more complex behavior of the field, namely the superposition of variations at the 22- and ~80-year timescales on a steady variation, as a result of superimposed surface effects of core processes at several timescales.
To improve the representation of the SV for time intervals around the extrema of the first time-derivative, the SV time series could be divided in segments approximated by second-order polynomials, according to zero values of the third time-derivative of the field and apply the technique described in the previous section, a1 being the acceleration and 2a2 the constant third time-derivative. However, in case of the data set available from European observatories, the piecewise fit of second degree polynomials to data, be they the field or its first time derivative, can be applied to map the internal field secular change, as was done in Section 3, only for a limited time interval (1960–2004), in which the observatory network providing data is dense enough. An alternative solution, using main field models at global (see recent reviews by Olsen et al. (2007) and Jackson and Finley (2007)) or at regional scales (Korte and Holme, 2003; Thébault, 2008; Verbanac et al., 2009), spanning a long enough time interval to get meaningful information on the secular variation, has potential in mapping the SV for areas and time intervals with a less dense distribution of observatory data. Among drawbacks of available models based only or mainly on observatory data that could be used in SV mapping are: assigning distorted information to areas or time spans uncovered with data and leakage of external signal into main field models. The latter aspect is discussed in the next section. As regards the first aspect, we acknowledge here that the recent versions of IGRF main filed models benefit from a much better geographical coverage as satellite data have been included in modeling. However, for the present study they have no relevance, because the smoothed time series used in our analysis end before satellite data were produced and integrated in models.
5. On the Leakage of External Signal into Main Field Models
Looking at data provided by main field models based on observatory data from the same angle we did in our discussion in the previous sections, reveals the presence of a reminiscent 11-year signal in the time series provided by the model.
In Fig. 10 differences between the model main field time series and filtered time series with an 11-year running window are shown for European observatories locations in case of horizontal component, for three main field models spanning long time intervals in the 20th century: gufm1 (Jackson et al., 2000, 1590-1990), IGRF-11 (Finlay et al., 2010, 1900-2010), and CM4 (Sabaka et al., 2004, 1960-2002). In case of IGRF the external signal leaked into the model is distorted by the 5 years sampling of the field, characteristic to this model. An external signal is present also in CM4 core field, in spite of the provision made for external variations in the construction of the model (Sabaka et al., 2004). We remind here that the 11-year signal includes, besides the direct external effect, the induced response to that.
As seen in the figure, the signal is significant (20 nT amplitude) and it becomes important in defining the secular variation using these models. For instance, in the time interval 1980–1990, a variation of about −4 nT/year would be added to the variation of the internal field, significantly altering the values and the pattern of the corresponding secular variation map, as Fig. 11 shows. In the latter the horizontal component isopore map for 1980–1985 based on the IGRF model is compared to the SV map for the same time interval for the internal field (i.e. with the 11-year signal removed). Displacements and shape changes of isopores can be noticed. The maps were obtained by interpolating model values in a grid of 2° × 2° latitude/longitude (see next section for details). It is also important to realize that the leakage of the external signal into main field models concern more or less all coefficients, including  , and
, and  that describe the magnetic moment of the dipole.
that describe the magnetic moment of the dipole.
6. A Discussion on the Secular Variation Evolution in the 20th Century in Europe
In this section the three main field models spanning long time intervals, namely gufm1 (1590–1990), IGRF-11 (the entire 20th century) and CM4 (1960–2002), are used to describe the secular variation.
Considering our previous result that in the main field evolution variations at the 22-year and ~80-year scales superimpose on a so-called steady variation (Demetrescu and Do-brica, 2005, 2013) we treated gufm1, IGRF-11 and CM4 time series computed in a grid of 2° × 2° latitude/longitude (“virtual observatories”, term coined by Mandea and Olsen (2006)) exactly in the same way we treated observatory data: after filtering out the external features from the time series, the 11-year smoothed time series (E11) is smoothed with a 22-year running averages filter, obtaining E22. The latter is further filtered with a 80-year running averages filter to obtain what we call the steady variation (E80). The differences E11 –; E22, denoted E (22), is the so-called 22-year variation, while E22 –E80 (E(80)) is the so-called ~80-year variation.
Maps for every 5 years between 1910 and 2000, obtained by interpolating values calculated for the grid of 2° × 2° latitude/longitude, were drawn for H, Z, D, and their corresponding secular variation, using gufm1, IGRF, and CM4. The internal field and the 22-year, the ~80-year and the steady ingredients were considered. Of these, in Fig. 12 we show, as an example for the case of IGRF, maps of the radial field (Z) and its ingredients at 1960, and in Fig. 13 corresponding maps of the first time derivative (1955–1960). Examining the maps allows several conclusions to be drawn:
-
the pattern and amplitudes of the field ingredients change in time. They are similar in gufm1, IGRF and CM4;
-
the amplitude of the field ingredients is quite different from each other. For instance, in case of Z, in the last 40 years the 22-year variation amplitude reaches 50 nT, the ~80-year variation amplitude reaches 400 nT, while the steady variation is of the order of 35-50,000 nT;
-
the amplitudes of the temporal change of various field ingredients (Ė(22), Ė(80), Ė(steady)) are of the same order of magnitude as that of external variations (e.g. a few tens of nT/year for the Z internal field and the steady part, of the order of several nT/year in case of the 22-year and of 10–20 nT/year in case of the ~80-year ingredients; compare to +4 or −4 nT/year of the external signal in certain time intervals such as 1970–1980 and, respectively, 1980–1990 for H and Z), hence the importance of properly eliminating the external signal before any interpretation of SV is done; - various field ingredients (E(22), E(80), E(steady)) evolve at different geographical scales as Demetrescu and Dobrica (2013) have shown at global scale (approximately 10–20, 30–40, and 60–100 degrees of latitude, respectively, in case of Z). The geographical pattern of the secular variation of the internal field (Ė11) at much smaller scales (country size) could be decided by the combination of the 22-year and the ~80-year variations.
7. Conclusions
We have discussed, based on data from the European observatory network and global main field models extending a long time interval (gufm1, 1590–1990, IGRF, 1900–2010; CM4, 1960–2002), a few issues regarding the secular variation and secular acceleration, with consequences on mapping them at regional scales.
We confirmed the well known presence in the annual means of geomagnetic elements of a 11-year solar-cycle-related (SC) signal due to incomplete averaging out external effects and their induced counterparts, modulated by solar activity (Chapman and Bartels, 1940; Yukutake, 1965; Bhargava and Yacob, 1969; Alldredge, 1975, 1976; Cour-tillot and Le Mouël, 1976; Alldredge et al., 1979; Yukutake and Cain, 1979; Demetrescu et al., 1988; Verbanac et al., 2007; Wardinski and Holme, 2011) and quantitatively showed that the time change of the signal is of the same order of magnitude as that of the internal ingredients of the measured field. As a consequence, the SC signal should be filtered out before any discussion on SV. An attempt to do that was reported by Verbanac et al. (2009), but they used “a single averaged external field approximation time series to be subtracted from each observatory data series”, while our approach used such time series determined for each observatory of the study. We also showed that the SC signal leaks into spherical harmonics models of the main field that are based only or mainly on observatory and repeat station data. That signal should be properly filtered out from data before modeling, as, for instance, Verbanac et al. (2009) did, or, in case of certain main field models such as gufm1, IGRF, CM4, filtered out from the model time series, in order to deal with an uncontaminated internal field, as we did.
A second issue is that unless the two induced fields by the core field, (1) by magnetic induction in the litosphere (the induced litospheric field) and (2) by electromagnetic induction in the conductive mantle and crustal structures, are independently known, only the change of the entire internal field can be obtained from data when the time derivative is considered.
A third issue was revealed by the time perspective offered by long series of observatory data. We demonstrated the inadecuacy of the jerk concept in general and in SV mapping in particular, when dealing with time series from which the external signal was filtered out. The internal field represented by such time series does no longer show a sharp variation at the jerk time. It shows a rather smooth transition, lasting several years, between episodes of increasing and decreasing or decreasing and increasing SV. Also, the secular acceleration would not be constant between its zero values as it is within the jerk concept. Unless the SV is strictly linear betweeen two successive extrema, the acceleration will have a pulse- or a more complex shape in that time interval. The jerks should be regarded as parts of a more complex behavior of the field, namely the superposition of variations at the 22- and ~80-year timescales on a steady variation, as a result of superimposed surface effects of core processes at several time scales.
A fourth issue regards the contribution of high-frequency ingredients of the SV to the observed geographical pattern of the SV. Depending on the map scale and size, different ingredients could decide that pattern. We found out, for instance, that page-size global maps, as those posted at http://www.ngdc.noaa.gov/wist/magfield.jsp, are dominated by the steady field variation, while regional maps as those of the present paper are influenced by the geographical pattern of the 22-year and ~80-year variations. SV patterns of country-size maps could be decided by the two high-frequency ingredients.
The results of the present paper contribute to a better understanding and interpretation of the secular variation temporal evolution and geographical distribution, and set new observational constraints for main and/or internal field modelling.
References
Alexandrescu, M., D. Gibert, G. Hulot, J.-L. Le Mouël, and G. Saracco, Detection of geomagnetic jerks using wavelet analysis, J. Geophys. Res., 100, 12557–12572, 1995.
Alexandrescu, M., V. Courtillot, and J.-L. Le Mouël, Geomagnetic field direction in Paris since the mid-sixteenth century, Phys. Earth Planet. Inter., 98, 321–360, 1996.
Alexandrescu, M., V. Courtillot, and J.-L. Le Mouël, High resolution secular variation of geomagnetic field in Western Europe over the last 4 centuries: Comparison and integration of hystorical data from Paris and London, J. Geophys. Res., 102, 20245–20258, 1997.
Alldredge, L. R., A hypothesis for the source of impulses in geomagnetic secular variation, J. Geophys. Res., 80, 1571–1578, 1975.
Alldredge, L. R., Effects of solar activity on annual means of geomagnetic components, J. Geophys. Res., 81, 2990–2996, 1976.
Alldredge, L. R., C. O. Stearns, and M. Sugiura, Solar cycle variation in geomagnetic external spherical harmonic coefficients, J. Geomag. Geoelectr., 31, 495–508, 1979.
Bhargava, B. N. and A. Yacob, Solar cycle response in the horizontal force of the Earth’s magnetic field, J. Geomag. Geoelectr., 21, 385–397, 1969.
Chapman, S. and J. Bartels, Geomagnetism, 1049 pp., Clarendon Press, Oxford, 1940.
Courtillot, V. and J.-L. Le Mouël, On the long-period variations of the Earth’s magnetic field from 2 months to 20 years, J. Geophys. Res., 81, 2941–2950, 1976.
Courtillot, V., J. Ducruix, and J-L. Le Mouël, Sur une accélération récente de la variation séculaire du champ magnétique terrestre, C. R. Hebd. S éances Acad. Sci. Paris, Sé r. D, 287, 1095–1098, 1978.
Demetrescu, C. and V. Dobrica, Recent secular variation of the geomagnetic field. New insights from long series of observatory data, Rev. Roum. Geophys., 49, 22–33, 2005.
Demetrescu, C. and V. Dobrica, High-frequency ingredients of the secular variation of the geomagnetic field. Insights from long series of observatory data, Geophys. J. Int., 2013 (submitted).
Demetrescu, C., M. Andreescu, and T. Nestianu, Induction model for the secular variation of the geomagnetic field in Europe, Phys. Earth Planet. Inter., 50, 261–271, 1988.
Finlay, C. C., S. Maus, C. D. Beggan, T. N. Bondar, A. Chambodut, T. A. Chernova, A. Chulliat, V. P. Golovkov, B. Hamilton, M. Hamoudi, R. Holme, G. Hulot, W. Kuang, B. Langlais, V. Lesur, F. J. Lowes, H. Luhr, S. Macmillan, M. Mandea, S. McLean, C. Manoj, M. Men-vielle, I. Michaelis, N. Olsen, J. Rauberg, M. Rother, T. J. Sabaka, A. Tangborn, L. Tøffner-Clausen, E. Thebault, A. W. P. Thomson, I. Wardinski, Z. Wei, and T. I. Zvereva, International Geomagnetic Reference Field: The eleventh generation, Geophys. J. Int., 183, 1216–1230, doi:10.1111/j.1365-246X.2010.04804.x, 2010.
Hemant, K. and S. Maus, Geological modeling of the new CHAMP magnetic anomaly maps using a geographical information system technique, J. Geophys. Res., 110, B12103, doi:10.1029/2005JB003837, 2005.
Hulot, G., N. Olsen, E. Thébault, and K. Hemant, Crustal concealing of small-scale core-field secular variation, Geophys. J. Int., 177, 361–366, doi:10.1111/j.1365-246X.2009.04119.x, 2009.
Jackson, A. and C. Finley, Geomagnetic secular variation and its applications to core, in Treatise on Geophysics, Ed.-in-Chief G. Schubert, 5, Geomagnetism, edited by M. Kono, 147–195, Elsevier, Amsterdam, 2007.
Jackson, A., A. R. T. Jonkers, and M. R. Walker, Four centuries of geomagnetic secular variation from historical records, Phil. Trans. R. Soc. Lond., 358, 957–990, 2000.
Korte, M. and R. Holme, Regularization of spherical cap harmonics, Geophys. J. Int., 153, 253–262, 2003.
Le Huy, M., M. Alexandrescu, G. Hulot, and J.-L. Le Mouël, On the characteristics of successive geomagnetic jerks, Earth Planets Space, 50, 723–732, 1998.
Mandea, M. and N. Olsen, A new approach to directly determine the secular variation from magnetic satellite observations, Geophys. Res. Let., 33, L15306, doi:10.1029/2006GL026616, 2006.
Mandea, M. and M. Purucker, Observing, modeling, and interpreting magnetic fields of the solid Earth, Surv. Geophys., 26, 415–459, doi:10.1007/s10712-005-3857-x, 2005.
Mandea, M., E. Bellanger, and J.-L. Le Mouël, A geomagnetic jerk for the end of 20th century?, Earth Planet. Sci. Lett., 183, 369–373, 2000.
Mayaud, P. N., Derivation, Meaning, and Use of Geomagnetic Indices, Geophys. Monogr. Ser., 22, 154 pp., AGU, Washington, D.C., 1980.
Mursula, K., I. Usoskin, and B. Zieger, On the claimed 5.5-year periodicity in solar activity, Sol. Phys., 176, 201–210, 1997.
Olsen, N., The electrical conductivity of the mantle beneath Europe derived from C-Responses from 3 h to 720 h, Geophys. J. Int., 133, 298–308, 1998.
Olsen, N., G. Hulot, and T. J. Sabaka, The present field, in Treatise on Geophysics, Ed.-in-Chief G. Schubert, 5, Geomagnetism, edited by M. Kono, 33–77, Elsevier, Amsterdam, 2007.
Sabaka, T. J., N. Olsen, and R. A. Langel, A comprehensive model of the quiet-time, near Earth magnetic field: Phase 3, Geophys. J. Int., 151, 32–68, doi:10.1046/j.1365-246X.2002.01774.x, 2002.
Sabaka, T. J., N. Olsen, and M. E. Purucker, Extending comprehensive models of the Earth’s magnetic field with ørsted and CHAMP data, Geophys. J. Int., 159, 521–547, doi:10.1111/j.1365-246X.2004.02421.x, 2004.
Thébault, E., A proposal for regional modeling at the Earth’s surface, R-SCHA2D, Geophys. J. Int., 174, 118–134, doi:10.1111/j.1365-246X.2008.03823x, 2008.
Thébault, E., K. Hemant, G. Hulot, and N. Olsen, On the geographical distribution of induced time-varying crustal magnetic fields, Geophys. Res. Lett., 36, L01307, doi:10.1029/2008GL036416, 2009.
Verbanac, G., H. Lühr, M. Korte, and M. Mandea, Contributions of the external field to the observatory annual means and proposal for their corrections, Earth Planets Space,59, 251–257, 2007.
Verbanac, G., M. Korte, and M. Mandea, Four decades of European geomagnetic secular variation and acceleration, Ann. Geophys., 52, 487–503, 2009.
Yukutake, T., The solar cycle contribution to the secular change in the geomagnetic field, J. Geomag. Geoelectr., 17, 287–309, 1965.
Yukutake, T. and J. C. Cain, Solar cycle variations of the first-degree spherical harmonic components of the geomagnetic field, J. Geomag. Geoelectr., 31, 509–544, 1979.
Wardinski, I. and R. Holme, Signal from noise in geomagnetic field modelling: denoising data for secular variation studies, Geophys. J. Int., 185, 653–662, 2011.
Acknowledgments
The paper is a result of the CNCSIS-UEFISCSU project IDEI, 151/2007. We acknowledge the activity of anonymous geomagnetic observatory operators and of the World Data Centers on Geomagnetism for obtaining and, respectively, keeping data used in this study. Parts of this paper were presented at the 8th IAGA General Assembly, Toulouse, 2005, and at the 33rd International Geological Congress, Oslo, 2008.
Author information
Authors and Affiliations
Corresponding author
Appendix.
Appendix.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dobrica, V., Demetrescu, C. & Stefan, C. Toward a better representation of the secular variation. Case study: The European network of geomagnetic observatories. Earth Planet Sp 65, 767–779 (2013). https://doi.org/10.5047/eps.2012.12.001
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.5047/eps.2012.12.001








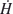 around 1919). This was also noticed by
around 1919). This was also noticed by 



