Cosmic Dust V
- Article
- Open access
- Published:
Far-infrared continuum absorption of olivine at low temperatures
Earth, Planets and Space volume 65, pages 1139–1143 (2013)
Abstract
The far-infrared continuum opacity of cold dust is an important quantity for the study of debris disks in planetary systems and of protoplanetary disks. Olivine is considered the most abundant crystalline dust species in such environments. We present spectroscopic absorption measurements on olivine plates of the order of a millimeter thickness at wavelengths between 60 and 400 μ m for temperatures down to 10 K. Our data reveal a strong temperature dependence of the continuum absorption coefficient, i.e. more than an order of magnitude decrease at 100 μ m for 10 K compared to room temperature. The absolute values are generally much lower than those measured with olivine powders embedded into polyethylene pellets, even if the difference between plate and powder samples is taken into account by theoretical models. In contrast to this, the room temperature data are in relatively good agreement with simulations using optical constants determined from reflection measurements. At low temperatures, the absorption coefficient of olivine was measurable with sufficient accuracy only up to 90 μ m for 10 K and up to 110 μ m for 100 K. These data reveal a drastic change in the spectral slope (from β ~ 2.0 to β > 5.0) for the continuum underlying the 69-μ m band, which is not predicted by the low-temperature optical constants determined for forsterite.
1. Introduction
Mg-rich olivine (general formula of olivine (Mg,Fe)2SiO4) is probably the most abundant silicate mineral in space. Because of its high thermal stability, it is one of the first minerals that condenses from a cooling gas of solar composition (Gail, 2003). The presence of olivine dust particles of sub-micron size has been detected by the infrared spectroscopy of thermally-emitted radiation from stellar outflows (e.g. Molster et al., 2002), protoplanetary disks (e.g. Juhász et al., 2010), and from warm dust in planetary systems (‘exozodiacal dust’, e.g. Olofsson et al., 2012). The search for olivine in colder environments with the Herschel space telescope has led to a number of detections of the 69-μ m olivine vibration band (e.g. Sturm et al., 2010; de Vries et al., 2012). From the composition-sensitive wavelength position of this band, it has been deduced that the olivines in these cases were Fe-poor (e.g. Sturm et al., 2013), close to the composition of the Mg end member of the olivine series, forsterite (Mg2SiO4). However, in planetary system dust, considerably more iron-rich olivine with an approximate Mg/(Mg + Fe) ratio of 0.8 (in the following, designated as Forsterite80% = Fo80) has been found (Olofsson et al., 2012).
Since infrared bands play the most important role in the diagnostics of dust minerals and can also serve as indicators of the dust temperature, laboratory studies have mostly concentrated on their investigation, examining the dependence of band positions, widths, and strengths on composition, grain size, grain shape, temperature, and structural perfectness (e.g. Koike et al., 2006, and references therein). Several of these studies have especially considered the far-infrared bands at about 50- and 70-μ m wavelengths. It has been proposed that the temperature dependence of their widths and positions makes them usable as a dust thermometer (Chihara et al., 2001; Bowey et al., 2002), which is indeed exploited today with Herschel spectra (e.g. de Vries et al., 2012). Most of the laboratory studies have been performed on powders of olivine and forsterite, while reflection measurements on polished crystals have been used in a few cases in order to determine the complex refractive index of natural olivine (Fabian et al., 2001) at room temperature, and of forsterite even at low temperatures down to 50 K (Suto et al., 2006).
Apart from the diagnostic lattice-vibration bands, the value of the continuum absorption coefficient in adjacent spectral ranges is also important. The absorption of stellar radiation, which determines the temperature of dust in stellar environments, takes place in spectral regions, where minerals are often only weakly absorbing (Zeidler et al., 2011; Pitman et al., 2013), except for conducting, or semiconducting, compounds. Similarly, if dust is located at a larger distance from a star, its thermal radiation may occur at very long infrared wavelengths extending significantly beyond the range of lattice-vibration bands where the emis-sivity is determined by a low continuum opacity as well. Observations at such far-infrared wavelengths (e.g. in the Herschel PACS 100-μ m and 160-μ m bands) are an important tool to study cold dusty structures, such as proto-planetary disks and debris disks (e.g. Eiroa et al., 2011). Consequently, opacity data of relevant dust species are of great importance in order to be able to convert the observed wavelength-dependent fluxes into dust masses, temperatures, and spatial distributions (e.g. Krivov et al., 2008).
Given the diversity of dust minerals, the inventory of spectroscopic data at these long wavelengths is still relatively poor. Some of the data used in models are uncertain due to the methods from which they are derived, or do not take into account the temperature dependence of the continuum opacity. For instance, optical constants derived from reflection measurements at these long wavelengths are actually extrapolations of the band profiles situated shortward and do not contain information about low-energetic continuum absorption processes (see e.g. Henning and Mutschke, 1997, and references therein). Since, for these processes, the imaginary part of the refractive index is typically two or more orders of magnitude smaller than the real part, reflectivity is not sensitive to them. Consequently, the continuum opacity can only be constrained by dedicated absorption measurements.
For olivines, previous far-infrared absorption measure-ments—as already mentioned—have mostly focused on the far-infrared bands and rarely discuss the continuum absorption. Exceptions are provided by Mennella et al. (1998) and Chihara et al. (2001), who performed also temperaturedependent measurements down to 24 K and liquid helium temperature, respectively. While Chihara et al. (2001) cover the wavelength range up to 100 μm (~70 μm at low temperatures), the measurements of Mennella et al. (1998) extend to 2 mm in wavelength. Both find a steepening of the absorption decay at a low temperatures. The absolute values of the absorption index at low temperature, however, differ significantly, which may result from the different samples (forsterite and Fo90 olivine, respectively, see Table 1). On the other hand, both investigations used powder samples embedded in polyethylene (PE) pellets for the measurements. Imai et al. (2009) have demonstrated that such data depend on the shape and the crystal quality (lattice defects) of the powder. In order to obtain data with less dependence on these factors, we present here measurements of the temperature-dependent absorption coefficient using bulk olivine plates. Powder measurements are carried out for comparison. Section 2 describes our measurement set-up and method. In Section 3 we present the absorption spectra obtained, and in Section 4, we discuss the derived temperature-dependent opacity values in relation to those obtained by other authors.
2. Measurements
We measured the absorption from two polished crystal plates, which were cut from olivine crystals from San Carlos (Arizona), having the composition Mg1.78Fe0.22SiO4. The thicknesses of the plates were 0.8 mm and about 3.6 mm, respectively. The plates were not crystallographi-cally oriented. Thus, an arbitrary mixture of contributions from vibrational excitations along all three crystal axes have been measured in the absorption spectra. However, we note that the continuum absorption coefficients, predicted by the optical constants published by Fabian et al. (2001) and Suto et al. (2006), are very similar for the principal crystallo-graphic directions. We assume that additional low-energetic excitations would not impose a strong anisotropy, and that the absorption coefficient averaged over the crystal orientations is a meaningful quantity within some limits.
The measurements have been performed with a Bruker 113v FTIR spectrometer using mylar beamsplitters of 12-μ m and 23-μ m thickness, a DTGS detector with PE window, and globar and Hg-lamp sources. This resulted in a wavelength range of 50 μ m to about 400 μ m, in which the spectra have been taken. The olivine samples were cooled down by a liquid helium continuous-flow cryostat with PE windows, inserted into the sample chamber of the spectrometer to measure the transmission through the samples. The cryostat allowed for the removal of the samples from the beam for reference measurements at each temperature. Measurements have been performed at room temperature, 200 K, 100 K, and 10 K for the thinner plate, and at 200 K, 150 K, 100 K, and 10 K for the thicker plate. At room temperature, the 3.6-mm plate was opaque in (more or less) the whole wavelength range.
Besides the absorption from the samples, additional losses to the transmitted spectrometer beam arose from the reflection at the plate surfaces. According to the optical constants derived by Fabian et al. (2001), the average refractive index at λ = 100 μ m of olivine is 2.66, resulting in a reflection loss of 20.6% per surface, which decreases slightly at longer wavelengths (about 19.7% at λ = 300 μ m) and increases slightly at shorter ones. These values depend slightly on the unknown orientation of the plates and have thus to be considered somewhat uncertain (by ±2%), consequently limiting the sensitivity of the measurements to small absorption losses.
Moreover, we found that an additional significant loss of intensity occurred with the thicker plate, which was due to refraction of the beam, caused by a slight non-parallelity of the plate surfaces 1 Footnote 1. Unfortunately, we were not able to determine the magnitude of this loss independently. It also cannot be excluded that the same effect has a small influence (≤3%) on the measurements with the thinner plate as well.
Both the refraction and reflection losses result in additive contributions to the derived absorption coefficient spectra. Consequently, we consider the data obtained with the thinner plate to be uncertain by a (wavelength- and temperature-independent) error of ±0.4–0.6 cm−1, the first value corresponding to the reflectivity error, the second to the possible refraction loss. Fortunately, there was sufficient overlap of the spectra measured with the thicker and thinner plates, so that we could normalize the former data to the latter at wavelengths where the values were a factor of 5 to 10 higher than the mentioned error limit. Identical additive corrections were applied to the spectra measured at all temperatures, resulting in a satisfactory agreement of the slopes of the spectra in the overlap region. Consequently, we assume the data obtained from the thicker plate to have approximately the same possible error of about 1 cm−1 (in this case corresponding to 20% transmission) after the normalization. However, this still means that the slope of the spectra and the absolute values are extremely uncertain at long wavelengths and at low temperatures (see the error bars in Fig. 1).
Measured and calculated absorption spectra of an olivine with Mg/(Mg + Fe) = 0.89 at different temperatures. The symbols are data measured on a 3.6 mm thick olivine plate while the solid lines are spectra measured with a 0.8 mm thick plate. The dotted lines indicate spectra measured on submicron-sized olivine grains embedded into PE pellets. The dashed line represents the calculated room-temperature absorption coefficient based on optical constants by Fabian et al. (2001), the dash-dotted line that for forsterite at 50 K after Suto et al. (2006), both for the average of the crystallographic orientations.
For comparison, we have measured the spectral absorption of hand-milled olivine powder embedded in polyethylene (PE) pellets from Imai et al. (2009) at low temperatures down to 10 K. We used one of their original pellets with a column density of σ = 2.83 mg/cm2 embedded at a mass ratio of 3.14 wt.% of olivine in PE. A pure PE pellet of the same thickness was used for measuring a reference spectrum, by which the sample transmission spectrum T (λ) was normalized.
3. Results
Figure 1 shows the resulting absorption spectra in terms of the linear absorption coefficient α. For the powder spectra, we have converted the mass absorption coefficient κ = ln(1/T)/σ into the linear absorption coefficient by multiplying with the mass density of olivine (ρ = 3.3 g/cm3) and dividing by a correction factor of f
e
= 0.776. This factor converts the linear absorption coefficient of bulk material into the volume-normalized absorption cross-section of ellipsoidal olivine particles (refractive index n = 2.66) embedded in PE (refractive index n
m
= 1.52) (CDE model- Bohren and Huffman, 1983), provided that the particles are only weakly absorbing
2
Footnote 2. Because the hand-milled olivine particles have irregular grain shapes according to Imai et al. (2009), we consider the CDE model to be appropriate. For spherical particles, the correction factor would be smaller  3
Footnote 3, resulting in increased α values.
3
Footnote 3, resulting in increased α values.
The comparison of the spectra reveals significant differences between bulk (olivine plate) data and pellet data. While the α-value measured at room temperature for the former is about 20 cm−1 at λ = 100 μ m (see Fig. 1), the value obtained for the pellet is higher by about a factor of 3.5. At 10 K and the same wavelength, we find α = (1.5 ± 1) cm−1 for the olivine plate, but a value around 35 cm−1 for the pellet, which is about 20 times higher. If these values are compared with calculated absorption coefficients based on the room-temperature optical constants by Fabian et al. (2001)—which result from Lorentzian oscillator fits to reflectivity measurements of olivine crystals—we find a relatively good agreement to the plate measurements. Actually, the reflectivity data give even smaller absorption coefficients (by a factor of 1.7, see Fig. 1, for averaged crystal orientation), for which one explanation could be that Fabian et al. measured an olivine with a lower iron content (Fo92, from Stubachtal, Austria). The forsterite data by Suto et al. (2006) would give a value which is even smaller by a factor of about 2.5 than that of the Fo92 olivine.
Consequently, the pellet data seem to suffer from additional losses, which amount here to 35–50 cm−1 in terms of ρ or to about 8–12 cm2/g in terms of κ (at λ = 100 μ m). We have to note that Imai et al. (2009) found lower mass absorption coefficients at λ = 100 μ m which were not reproduced by our measurements. At shorter wavelengths the data coincide, but beyond the 70-μ m absorption band the absorption falls more steeply in their data. This reflects the fact that, at these longer wavelengths, the absorption of these pellet samples is already quite small, so that it becomes sensitive, for example, to the reference values. We did not use exactly the same reference pellet as Imai et al. (2009), so that deviations are likely to arise from this difference in the procedure. The absorption coefficient obtained by Imai et al. (2009) at λ = 100 μ m amounts to about 23 cm−1 at room temperature (if translated into α-values), which is almost the same as the bulk value measured with the plates. Although, at shorter wavelengths, the big difference between pellet and bulk measurements is definitely valid (a factor of about 3 at λ = 70 μ m, also with the Imai et al. data), a steep decrease beyond this wavelength is not excluded. This uncertainty does of course also affect the 10-K spectrum at these longer wavelengths.
4. Discussion
In Table 1, we present a comparison of mass absorption coefficient data obtained by different authors. Data for olivines of different compositions are included, among them also data for pure forsterite measured by Suto et al. (2006) in reflection, and Chihara et al. (2001) measured as a powder in PE pellets. The data have been calculated (or corrected) again for the case of ellipsoidal particles (CDE model), this time assuming a vacuum environment and expressing them as the mass-normalized absorption coefficient (thus divided by the mass density of ρ = 3.3 g/cm3 for olivine). Other pellet data are from Fabian et al. (2001) and Mennella et al. (1998). All the pellet data have been read from graphs in the respective publications, in the case of Chihara et al. (2001) with a small extrapolation done simply by eye from 80-μ m to 100-μ m wavelength. Then, these data have been corrected for the influence of the embedding material (PE) by a factor of 0.765, resulting from the correction factors for embedded and non-embedded ellipsoidal particles of f
e
= 0.776 (see above) and f
ne
= 0.594
4
Footnote 4. We note that for spherical particles  and
and  , which means that the measured absorption of embedded spherical particles is almost equal to that of non-embedded ellipsoidal particles, while the values for non-embedded spherical particles would be smaller by about a factor of 2.
, which means that the measured absorption of embedded spherical particles is almost equal to that of non-embedded ellipsoidal particles, while the values for non-embedded spherical particles would be smaller by about a factor of 2.
The values in Table 1 are given with a very low precision, taking into account the inexact way of reading from the figures and the extrapolations. However, they show clearly that bulk data result in much lower absorption coefficients than measured powder spectra. Imai et al. (2009) have demonstrated that irregular grain shapes and lattice distortion introduced by the production of small particles are reasons for increased long-wavelength absorption in powder measurements. However, irregular grain shapes are taken into account by the CDE model in our calculated data. Somewhat higher κ values could be imagined for very elongated grain shapes, but not above the limit of bulk absorption (f ne = 1.0). For the influence of lattice distortion, we note that the hand-milled olivine should have a relatively low lattice distortion, but we cannot exclude that the increased absorption of the powders originates from this effect.
The strong discrepancy between room-temperature pellet spectra and spectra simulated from their reflectivity data had also been noted by Fabian et al. (2001). In their data which extended to 100 μ m in wavelength, they did not see a steep decrease in absorption beyond 70 μ m as did Imai et al. (2009). At 100 μ m, they obtained a factor of 20 enhancement (after correction for the PE’s influence) with the pellets. They assigned this difference tentatively to scattering losses caused by agglomeration of the grains or by boundaries in the pellet. Agglomeration effects on far-infrared spectra had been modeled by Stognienko et al. (1995). They find enhancement factors of up to 3.5 for compact silicate aggregates, which is in agreement with our room-temperature results, but not with those of Fabian et al. and not with our results at low temperatures. Scattering from the polyethylene matrix may thus be another major contribution, although warm-pressed PE pellets are rather homogeneous. We suggest that this enhancement effect should be studied more thoroughly if pellets continue to be used for continuum opacity measurements in future.
The 100-μ m mass absorption coefficient derived from our olivine-plate measurements shows the largest decrease at 10 K compared with 300 K of all data in Table 1. This decrease is connected with an extreme steepening of the spectrum in the wavelength range 50–100 μ m (see Fig. 1). Chihara et al. (2001) have noted such a steepening also in their powder measurements of forsterite. At liquid helium temperature, they derive a power-law exponent of about β = 5.0 for the spectral dependence. In our data, the slope is even steeper in this wavelength range. This could be related to the long-wavelength wings of the lattice-vibration bands at shorter wavelengths (especially at 33 μ m and 50 μ m) and should probably not be taken as a continuum slope. The mentioned bands sharpen at lower temperatures and shift to shorter wavelengths, which will likely result in a steepening of the spectrum in the range of their long-wavelength wings. The slope in this wavelength range may therefore strongly depend on the orientation of the crystal. Unfortunately, we cannot check this effect for olivine by simulations because low-temperature optical constants are not available. When using the optical constants of forsterite at 50 K by Suto et al. (2006), we do not observe this effect (see Fig. 1). However, forsterite bands are located at shorter wavelengths and are somewhat sharper, so that their long-wavelength wings may be of less influence. We are unable to clarify this issue at the present time.
On the other hand, we have to expect that phonon-difference processes 5 Footnote 5 may contribute to the far-infrared absorption. These contributions should disappear at low temperatures due to freezing of the phonon excitations. They may account for part of the deviation of our room-temperature data from the spectrum simulated from the reflectivity-based Lorentzian oscillator model. In our room-temperature data, the spectral slope appears to be somewhat shallower than the β = 2.0 of the oscillator model. At 200 K and 150 K, it seems to converge to β ~ 2.0 for wavelengths beyond 100 μ m. Whether this remains true for lower temperatures, as the forsterite oscillator model suggests, cannot yet be decided because of the limitations in our data (see Section 2). They are so far both consistent with β = 2.0, or with a steeper slope at λ < 100 μ m.
5. Conclusions
The far-infrared continuum spectrum of olivine is still not well understood. Transmission measurements of thin plates result in much lower absorption coefficients than measurements of powders embedded in PE pellets and may provide more reliable absorption index data. The spectral range below 100 μ m requires further investigations to clarify the origin of the very steep spectral slope measured at low temperature. For the range above 100 μ m, it is not yet known whether this steep slope will continue, or whether it will change to the value of β = 2.0 that is usually assumed based on Lorentzian oscillator models. However, it has to be expected that low-energetic excitations need to be considered, in addition to these models. Measurements on olivine plates with a thickness of centimeters may be required in further studies.
If the emissivity of olivine is confirmed to be as small as derived from the plate measurements, olivine will hardly contribute to the emission of cold dust mixtures if, for example, amorphous silicates are present as well. Vice versa, crystalline olivine dust could be perfectly hidden behind the thermal emission of other cold dust components.
Notes
1This was discovered by a non-reproducible signal after removing and remounting the sample, due to different degrees of deflection of the beam depending on the orientation of the sample, it happened only with the thicker plate.
2Within this limit, the volume-normalized absorption cross-section of embedded particles in the CDE model is given by
 , while the bulk linear absorption coefficient is k × Im(ϵ)/n, with k being the wavenumber.
, while the bulk linear absorption coefficient is k × Im(ϵ)/n, with k being the wavenumber.3For spherical particles, the volume-normalized absorption cross-section of weakly absorbing embedded particles is
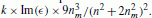 .
.4This value is simply obtained by setting n m = 1 in the formula for f e (footnote 2).
5Phonon-difference process: excitation of a lattice vibration mode during the simultaneous destruction of a lower-energetic one, allowed by the anharmonic lattice potentials, see Henning and Mutschke (1997).
References
Bohren, C. F. and D. R. Huffman, Absorption and Scattering of Light by Small Particles, John Wiley, New York, 1983.
Bowey, J. E., M. J. Barlow, F. J. Molster, A. M. Hofmeister, C. Lee, C. Tucker, T. Lim, P. A. R. Ade, and L. B. F. M. Waters, The 69-μ m forsterite band as a dust temperature indicator, Mon. Not. R. Astron. Soc,331, L1–L6, 2002.
Chihara, H., C. Koike, and A. Tsuchiyama, Low-temperature optical properties of silicate particles in the far-infrared region, Publ. Astron. Soc. Jap.,53, 243–250, 2001.
de Vries, B. L., B. Acke, J. A. D. L. Blommaert, C. Waelkens, L. B. F M. Waters, B. Vandenbussche et al., Comet-like mineralogy of olivine crystals in an extrasolar proto-Kuiper belt, Nature,490,74, 2012.
Eiroa, C, J. P. Marshall, A. Mora, A. V. Krivov, B. Montesinos, O. Absil, D. Ardila, M. Arévalo, J.-Ch. Augereau, and A. Bayo, Herschel discovery of a new class of cold, faint debris discs, Astron. Astrophys.,536, L4, 2011.
D. Ardila, M. Arévalo, J.-Ch. Augereau, and A. Bayo, Herschel discovery of a new class of cold, faint debris discs, Astron. Astrophys.,536, L4, 2011.
Fabian, D., T. Henning, C. Jäger, H. Mutschke, J. Dorschner, and O. Wehrhan, Steps toward interstellar silicate mineralogy. VI. Dependence of crystalline olivine IR spectra on iron content and particle shape, Astron. Astrophys.,378, 228–238, 2001.
Gail, H.-P, Formation and evolution of minerals in accretion disks and stellar outflows, in Astromineralogy, edited by Th. Henning, 55 pp., Springer, Berlin, 2003.
Henning, T. and H. Mutschke, Low-temperature infrared properties of cosmic dust analogues, Astron. Astrophys.,327,743–754, 1997.
Imai, Y, C. Koike, H. Chihara, K. Murata, T. Aoki, and A. Tsuchiyama, Shape and lattice distortion effects on infrared absorption spectra of olivine particles, Astron. Astrophys.,507, 277–281, 2009.
Juhász, A., J. Bouwman, Th. Henning, B. Acke, M. E. van den Ancker, G. Meeus, C. Dominik, M. Min, A. G. G. M. Tielens, and L. B. F. M. Waters, Dust evolution in protoplanetary disks around Herbig Ae/Be stars? the Spitzer view, Astrophys. J.,721, 431–455, 2010.
Koike, C, H. Mutschke, H. Suto, T. Naoi, H. Chihara, Th. Henning, C. Jäger, A. Tsuchiyama, J. Dorschner, and H. Okuda, Temperature effects on the mid-and far-infrared spectra of olivine particles, Astron. Astrophys.,449, 583–596, 2006.
Krivov, A. V, S. Muller, T. Löhne, and H. Mutschke, Collisional and thermal emission models of debris disks: Toward planetesimal population properties, Astrophys. J.,687, 608–622, 2008.
Mennella, V, J. R. Brucato, L. Colangeli, P. Palumbo, A. Rotundi, and E. Bussoletti, Temperature dependence of the absorption coefficient of cosmic analog grains in the wavelength range 20 microns to 2 millimeters, Astrophys. J.,496, 1058–1066, 1998.
Molster, F J., L. B. F M. Waters, A. G. G. M. Tielens, C. Koike, and H. Chihara, Crystalline silicate dust around evolved stars. III. A correlations study of crystalline silicate features, Astron. Astrophys.,382, 241–255, 2002.
Olofsson, J., A. Juhász, Th. Henning, H. Mutschke, A. Tamanai, A. Moór, and P. Ábrahám, Transient dust in warm debris disks. Detection of Fe-rich olivine grains, Astron. Astrophys.,542, A90, and 547, C1, 2012.
Pitman, K. M., A. M. Hofmeister, and A. K. Speck, Revisiting astronomical crystalline forsterite in the UV to near-IR, Earth Planets Space,65, 129–138, 2013.
Stognienko, R., T. Henning, and V Ossenkopf, Optical properties of coagulated particles, Astron. Astrophys.,296,797, 1995.
Sturm, B., J. Bouwman, Th. Henning, N. J. Evans, B. Acke, G. D. Mulders, L. B. F. M. Waters, E. F. van Dishoeck, G. Meeus, J. D. Green et al., First results of the Herschel key program “Dust, Ice and Gas In Time” (DIGIT): Dust and gas spectroscopy of HD 100546, Astron. Astrophys.,518, L129, 2010.
Sturm, B., J. Bouwman, Th. Henning, N. J. Evans, L. B. F. M. Waters, E. F. van Dishoeck et al., The 69 μ m forsterite band in spectra of protoplanetary disks. Results from the Herschel DIGIT programme, Astron. Astrophys.,553, A5, 2013.
Suto, H., H. Sogawa, S. Tachibana, C. Koike, H. Karoji, A. Tsuchiyama, H. Chihara, K. Mizutani, J. Akedo, K. Ogiso et al., Low-temperature single crystal reflection spectra of forsterite, Mon. Not. R. Astron. Soc,370, 1599–1606, 2006.
Zeidler, S., T. Posch, H. Mutschke, H. Richter, and O. Wehrhan, Near-infrared absorption properties of oxygen-rich stardust analogs. The influence of coloring metal ions, Astron. Astrophys.,526, A68, 2011.
Acknowledgments
We thank Gabriele Born, Walter Teuschel, and Dirk Fabian for preparational work and help with the measurements. We are grateful to Yuta Imai for providing his samples for comparison measurements. H. M. and S. Z. gratefully acknowledge support by the Deutsche Forschungsgemeinschaft by grant MU 1164/7 within the priority programme “The First 10 Million Years of the Solar System”.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mutschke, H., Zeidler, S. & Chihara, H. Far-infrared continuum absorption of olivine at low temperatures. Earth Planet Sp 65, 1139–1143 (2013). https://doi.org/10.5047/eps.2013.07.003
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.5047/eps.2013.07.003

 , while the bulk linear absorption coefficient is k × Im(ϵ)/n, with k being the wavenumber.
, while the bulk linear absorption coefficient is k × Im(ϵ)/n, with k being the wavenumber.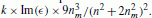 .
.