Swarm Science Data Processing and Products
- Article
- Open access
- Published:
Determination of the 3-D distribution of electrical conductivity in Earth’s mantle from Swarm satellite data: Frequency domain approach based on inversion of induced coefficients
Earth, Planets and Space volume 65, pages 1247–1256 (2013)
Abstract
Mapping the three-dimensional (3-D) electrical conductivity of Earth’s mantle has been identified as one of the primary scientific objectives for the Swarm satellite mission. We present a 3-D frequency domain inversion scheme to recover mantle conductivity from satellite magnetic data. The scheme is based on an inversion of time spectra of internal (induced) spherical harmonic coefficients of the magnetic potential due to magnetospheric sources. Time series of internal and external (inducing) coefficients, whose determination is a prerequisite for this formulation, will be available as a Swarm Level-2 data product. An iterative gradient-type (quasi-Newton) optimization method is chosen to solve our 3-D non-linear inverse problem. In order to make the inversion tractable, we elaborate an adjoint approach for a fast and robust calculation of the data misfit gradient. We verify our approach with synthetic, but realistic time spectra of internal coefficients, obtained by simulating induction due to a realistic magnetospheric source in a 3-D conductivity model of the Earth. In these model studies, both shape and conductivity of a large-scale conductivity anomaly in the mid-mantle are recovered very well. The inversion scheme also shows to be robust with respect to noise and is therefore ready to process Swarm data.
1. Introduction
Mapping the three-dimensional (3-D) electrical conductivity of Earth’s mantle has been identified as one of the primary scientific objectives for the Swarm multi-satellite geomagnetic mission (Friis-Christensen et al., 2006). An improved knowledge of the mantle conductivity provides an advanced understanding of the mantle’s chemical and physical properties and reflects the connectivity of constituents such as graphite, fluids and partial melt. Global 3-D electromagnetic (EM) induction studies can thus provide complementary information to global seismic tomography (e.g. Becker and Boschi, 2002; Romanowicz, 2003), which is used to ascertain the mantle’s bulk mechanical properties.
Regarding the EM technique, only recent improvements in global 3-D EM forward modelling and the growth of computational resources have made rigorous 3-D EM inversions on a global scale tractable. A few spherical 3-D inverse solutions have been developed recently (Koyama, 2001; Kelbert et al., 2008; Tarits and Mandea, 2010; Kuvshinov and Semenov, 2012), providing the first global and semi-global 3-D mantle conductivity models (Fukao et al., 2004; Koyama et al., 2006; Kelbert et al., 2009; Utada et al., 2009; Tarits and Mandea, 2010; Shimizu et al., 2010; Semenov and Kuvshinov, 2012). Recent progress in global 3-D forward and inverse modelling is summarized in two review papers by Kuvshinov (2008, 2012).
All mentioned 3-D models have been obtained by inverting data from the ground-based global network of geomagnetic observatories, and are based (except for the work of Tarits and Mandea, 2010) on analysis of C-responses (Banks, 1969). Although differing in details, the recovered global 3-D images reveal a substantial level of lateral heterogeneity in the mantle at depths between 410 and 1600 km; conductivity varies laterally by more than one order of magnitude between resistive and conductive regions.
However, bearing in mind that geomagnetic observatories are sparsely and irregularly distributed with large gaps in oceanic regions and the southern hemisphere, an interpretation of the 3-D inversion results in many regions requires extreme care. A lack of observations precludes any conclusive inferences about conductivity distributions in these regions. Moreover, in spite of continuing efforts to improve the coverage by long-term measurements in those regions (Shimizu and Utada, 1999; Chulliat et al., 2009; Korte et al., 2009; Matzka et al., 2009; Toh et al., 2010; among others), reliable images of 3-D variations of mantle conductivity in oceanic regions and as a whole in the southern hemisphere can hardly be obtained at present or in the foreseeable future with the use of ground-based data alone.
In contrast to ground-based data, measurements from low-Earth-orbit (LEO) platforms provide an excellent spatial coverage with data of uniform quality. However, to date, all practical inversions of existing satellite data have been for 1-D (or at most for 2-D) conductivity models (e.g. Constable and Constable, 2004; Kuvshinov and Olsen, 2006; Velímský et al., 2006; Martinec and Velímský 2009; Velímský, 2010). The main reason is that the analysis of satellite data is more challenging than the analysis of observatory data, since LEO satellites move typically with a speed of 7—8 km/s and thus, in reality, measure a mixture of temporal and spatial changes of the geomagnetic field. Another reason is that the orbital configurations of recent single satellite missions (Ørsted, CHAMP and SAC-C) are far from optimal in the context of 3-D mantle conductivity studies.
With the Swarm satellite mission, reliable global images of 3-D mantle heterogeneities, especially in regions with poor ground-based coverage, come into reach. The forthcoming mission has prompted the initiation of efforts to develop methodologies for recovering 3-D electrical conductivity variations from space. The net results of these coordinated studies supported by ESA are summarized in the report by Kuvshinov et al. (2010). One of the initial ideas was to use the C -response formalism to interpret satellite data (Kuvshinov et al., 2006), but benchmarking studies showed that the 3-D inversion of satellite C-responses does not yield satisfactory results (Kuvshinov et al., 2010).
In this paper, we describe an alternative approach, based on an inversion of time spectra of internal (induced) spherical harmonic expansion (SHE) coefficients of the magnetic potential that describes the signals of magnetospheric origin. A necessary condition for this approach is the determination of the time series of these and the corresponding external (inducing) coefficients. Both time series will be available as Swarm Level-2 data product from the Comprehensive Inversion (CI, Sabaka et al., 2013), which aims to separate magnetic contributions from various sources (originating in the core, lithosphere, ionosphere, and magneto-sphere) in the form of corresponding SHE coefficients. An approach to recover 3-D mantle conductivity from these data in time domain is described in the companion paper by Velímský (2013).
In Section 2 of this paper, we outline the equations governing global induction, introduce the theoretical concept that forms the basis of our inversion scheme and formulate an “adjoint” approach to efficiently compute the data misfit gradient. In Section 3, we describe how we implemented the concept numerically. Results obtained in model studies with this implementation are presented in Section 4. In Section 5, we summarize the work and give an outlook on planned future improvements.
2. Theoretical Concept
In this section, we first consider the solution of the EM forward problem, which involves the prediction of the EM fields induced by a given time-varying magnetospheric source in a given conductivity model of the Earth (Section 2.1). We then formulate the inverse problem of conductivity recovery as an optimization problem and introduce the relevant terms in Section 2.2. In order to efficiently compute the gradient of the data misfit, we focus on presenting the concept of an adjoint approach in Section 2.3.
2.1 Sketch of the forward problem
In frequency domain, Maxwell’s equations read



Here, B(r, ϑ, φ) and E(r, ϑ, φ) are magnetic and electric fields, respectively, and jext(r, ϑ, φ) is an impressed source current, with r, ϑ, and φ being distance from Earth’s centre, colatitude and longitude, respectively. σ (r, ϑ, φ) is the spatial conductivity distribution in the Earth,  , and γ0 is the magnetic permeability of free space. Note that the dependence of B, E and jext on angular frequency ω is omitted but implied. Also note that we adopt the Fourier convention
, and γ0 is the magnetic permeability of free space. Note that the dependence of B, E and jext on angular frequency ω is omitted but implied. Also note that we adopt the Fourier convention

In the source-free region above the conducting Earth, but below the magnetosphere, Eq. (1) reduces to ∇ × B = 0. B is thus a potential field and can be written as gradient of the magnetic potential V, i.e.

Equations (3) and (5) combine to Laplace’s equation,

The general solution of Eq. (6) can be represented as sum of external and internal parts, V = Vext + Vint, which read


Here, a is Earth’s mean radius,  and
and  are the expansion coefficients of the external (inducing) and internal (induced) parts of the potential, and
are the expansion coefficients of the external (inducing) and internal (induced) parts of the potential, and  is the spherical harmonic of degree n and order m,
is the spherical harmonic of degree n and order m,

with  being the Schmidt quasi-normalized associated Legendre polynomial of degree n and order ǀmǀ. Note that in Eqs. (7)–(8), we use different indices for external and internal coefficients to account for the 3-D structure. In a 3-D Earth model, every external coefficient
being the Schmidt quasi-normalized associated Legendre polynomial of degree n and order ǀmǀ. Note that in Eqs. (7)–(8), we use different indices for external and internal coefficients to account for the 3-D structure. In a 3-D Earth model, every external coefficient  induces a whole series of internal coefficients
induces a whole series of internal coefficients  , such that
, such that

where  is a transfer function we refer to as “matrix Q-response” or “Q-matrix”. Note also that here and in the following, we for simplicity use the conventions
is a transfer function we refer to as “matrix Q-response” or “Q-matrix”. Note also that here and in the following, we for simplicity use the conventions

In order to solve the coupled Eqs. (1) and (2) inside the conducting Earth, the impressed current jext has to be known. Our inducing magnetospheric current can be considered in the form of a spherical harmonic expansion of an equivalent sheet current, which is assumed to flow in a shell at r = a (embedded in an insulator) and produces exactly the external magnetic field Bext = −∇Vext at r = a. For a derivation see e.g. Kuvshinov and Semenov (2012), Appendix G. jext can then be written as

Here, δ(r −a) is Dirac’s delta function, e r is the outward unit vector, and ∇⊥ is the angular part of the gradient operator.
2.2 Inverse problem
We formulate the inverse problem of conductivity recovery as an optimization problem, i.e. we want to minimize a penalty function ϕ(m, λ) given as

with ϕ d being the data misfit and λ and ϕ s being a regular-ization parameter and a regularization term, respectively.
The data misfit ϕ d (m) is conventionally written as

where d is the data vector, here composed of the experimental (observed) internal coefficients, m is the model vector, and F is the functional solving the forward problem. The model vector m is composed of the N m model parameters, which in our case describe the conductivity structure of Earth’s mantle. C d is the data covariance matrix, and superscript † denotes hermitian matrix transpose. Usually, C d is assumed to be diagonal (i.e. to contain only the squared uncertainties of the experimental internal coefficients). Thus, we can rewrite Eq. (14) in the following form:

In this representation, ϕd(m) is the weighted sum (over all harmonics and a set of frequencies Ω) of the squared differences between experimental (observed) and predicted (modeled) internal coefficients, with the uncertainties  serving as weights.
serving as weights.
The regularization term ϕ s (m) is conventionally written as

where C
m
is the model covariance matrix, and superscript ⊤ denotes matrix transpose. It is often more convenient not to define C
m
, but the regularization matrix W, such that  . With this definition, we can rewrite Eq. (16) as
. With this definition, we can rewrite Eq. (16) as

W is supposed to smooth the solution, its form depends on the desired level of smoothness and the parameterization of the model.
Due to the non-linearity and the large size of 3-D EM inverse problems, iterative gradient-type methods (e.g. Nocedal and Wright, 2006) are typically the methods of choice. These methods require a computation of the gradient of the penalty function ϕ with respect to the model parameters, i.e.

While the gradient of the regularization term is easily calculated analytically and given by

the calculation of the data misfit gradient is more challenging. The straightforward option—brute-force numerical differentiation—requires extremely high computational loads and is approximate by nature. A much more efficient and elegant way to rigorously calculate the gradient of the misfit is provided by an adjoint approach, see e.g. Dorn et al. (1999). It allows the calculation of the misfit gradient for the price of only a few additional forward calculations (i.e. numerical solutions of Maxwell’s equations) excited by a specific (adjoint) source. Each inverse problem setting requires the finding of explicit formulas for the adjoint source. In the following subsection, we provide these formulas for our inverse problem formulation, following the general derivation by Pankratov and Kuvshinov (2010).
2.3 Adjoint approach
By differentiating Eqs. (7) and (8) with respect to r and setting r = a, we obtain the external and internal parts of the radial component of the magnetic field at Earth’s surface, respectively:


Since  , we can solve these equations for the (predicted) internal coefficients by making use of the orthogonality of the spherical harmonics
, we can solve these equations for the (predicted) internal coefficients by making use of the orthogonality of the spherical harmonics  :
:

Here, ds = sinϑdϑdφ, r = (r = a,ϑ,φ), the upper asterisk of  denotes complex conjugation, and
denotes complex conjugation, and  is the squared norm of the spherical harmonic
is the squared norm of the spherical harmonic  . Note that
. Note that  depends only on the external current source jext, which can be directly verified from Eqs. (12) and (20). B
r
, however, also depends on Earth’s conductivity structure (and thus on m).
depends only on the external current source jext, which can be directly verified from Eqs. (12) and (20). B
r
, however, also depends on Earth’s conductivity structure (and thus on m).
Taking the total derivative of the data misfit in Eq. (15) yields

where  means real part. Since
means real part. Since  is given by Eq. (22), the only term left to derive is
is given by Eq. (22), the only term left to derive is  . We first note that, by taking the derivative of Eq. (22), we obtain
. We first note that, by taking the derivative of Eq. (22), we obtain

where we define

The critical element in Eq. (24) is the total derivative of the radial component of the magnetic field, dB r . To investigate this element, let us first define the operator Gej (jext) as the “electric field solution” of Maxwell’s equations (1)–(2) for the current source j>ext, i.e. E = Ej = Gej(jext). Analogously, the operator Gbj (jext) represents the “magnetic field solution” of Maxwell’s equations (1)–(2). Note that these operators are universal and do not depend on the actual forward engine. In a similar way, we can define Geh(hext) as the electric field solution of a modified set of Maxwell’s equations for the fictitious “magnetic source” hext,


Let us now consider Maxwell’s equations (1)–(2) in an Earth’s model with infinitesimally changed conductivity σ + dσ, yielding electric and magnetic fields E + dE and B + dB, respectively:


Now subtract Eqs. (1)–(2) from Eqs. (28)–(29):


Using the operators defined above, we can rewrite Eq. (30) as

Note that we neglected the second order quantity dσdE. Equations (32) and (31) constitute a set of Maxwell’s equations for the infinitesimal fields dE and dB excited by the “source” dσGej(jext). Using the operator representation a second time, we obtain an expression for dB:

An important property of the operators Gej, Geh and Gbj are their reciprocity relations (Pankratov and Kuvshinov, 2010):


where

denotes a complex-valued bilinear scalar product. In a spherical coordinate system,

Making use of reciprocity relation (35) and the definitions above, Eq. (24) can be rewritten in operator form:

where

is a fictitious magnetic source, consisting of radial magnetic dipoles distributed along Earth’s surface with weights that are equal to  .
.
Substituting the last line of Eq. (38) into Eq. (23) yields

with

With the definition of the bilinear scalar product (37), we can use Eq. (40) to obtain the elements of the data misfit gradient:

where Eu = Geh(u). This representation implies a model built from elementary volume cells V j each having a piecewise constant conductivity σ j . The last term in Eq. (42), ∂σ j /∂m i , depends on the model parameterization (cf. Pankratov and Kuvshinov, 2010); note that the Einstein summation convention is implied for j. If the model parameters directly represent the conductivites of each cell, i.e. m i = σ i , then ∂σ j /∂m i = δ ij , where δ ij is Kronecker’s delta. Equation (42) demonstrates the essence of the adjoint approach: in order to calculate the gradient of the data misfit, only one (per frequency) additional forward modeling with excitation by the adjoint source u is required.
3. Numerical Implementation
So far, we presented very general derivations, starting from Maxwell’s equations and ending up with the gradient of the penalty function, which is required in gradient-type inversion schemes. These derivations neither depend on the choice of the forward engine (which solves Maxwell’s equations (1)–(2) for a given conductivity model and a given source) nor on the optimization method used to solve the inverse problem. In this section, we specify the model parameterization and the methods we used for the model studies presented in Section 4. The same implementations are planned to be used to analyse actual data of the Swarm satellite mission.
3.1 Forward computations
For forward computations, the 3-D conductivity structure σ is discretized on a regular spherical grid, consisting of n r × nϑ × nφ cells. The conductivity within each elementary volume cell is constant, thus satisfying the condition imposed by Eq. (42). In order to predict electric and magnetic fields generated both by a current source jext and by an adjoint source u, we use a contracting integral equation approach (extensively described in the paper by Kuvshinov and Semenov, 2012).
The most expensive part of the forward solution in terms of computational cost is the calculation of Green’s tensors. This has been implemented in an efficient way within the inversion algorithm. Since the Green’s tensors are independent of the 3-D model (Kuvshinov and Semenov, 2012), their computation has been isolated from the rest of the forward engine and does not need to be repeated in each iteration of the inversion scheme. A parallelization with respect to frequencies ω ϵ Ω has been implemented for a further acceleration of the calculations.
3.2 Inverse parameterization
The inversion domain is divided into Nr layers of possibly variable thicknesses. Since our data are coefficients of the SHE of the magnetic potential, it is most natural to also parameterize the model domain in terms of spherical harmonics, as it has been done previously by e.g. Kelbert et al. (2008). Within each layer, conductivity is thus defined as a finite sum of spherical harmonics up to a cut-off degree L, i.e. the number of model parameters N m is given by N m = N r × (L + 1)2. Note that N r does not necessarily coincide with the number of laterally heterogeneous layers n r relevant for forward modeling, as we might only try to resolve the conductivity structure of specific layers.
We first normalize the conductivity of each cell by defining

where ca > 0 and c b > 0 are chosen such that s ∈ [−1; 1] based on assumptions about minimum and maximum conductivities in the mantle. Note that inverting for s instead of σ also constrains the solution to be positive, since solving Eq. (43) for σ yields

We then write s for each layer as a sum of spherical harmonics,

with p and q being degree and order of the spherical harmonics and  being Schmidt quasi-normalized associated Legendre polynomials. The model vector m is accordingly composed of the coefficients of the SHE,
being Schmidt quasi-normalized associated Legendre polynomials. The model vector m is accordingly composed of the coefficients of the SHE,

Its constituents are easily found by inverting Eq. (45), making use of the orthogonality of the spherical harmonics, i.e.


where  is the squared norm of the associated Legendre polynomial
is the squared norm of the associated Legendre polynomial  .
.
In order to compute the data misfit gradient, the model-dependent term ∂σ j /∂m i needs to be known, cf. Eq. (42). For the model parameterization introduced above, this term is given by



The regularization matrix W introduced in Section 2.2 serves as smoothing operator. Radial smoothing, i.e. regularization across layer boundaries, is applied by a finite difference approximation of the vertical gradient (acting on the respective spherical harmonic coefficients). Within each layer, lateral smoothing consists of down weighting spherical harmonics of higher degrees by multiplication with a factor pβ, where β > 0 is chosen independently from the bulk regularization parameter λ. However, tests have shown that a variation of β is essentially equivalent to a variation of λ; thus fixing β to a moderate value, e.g. β = 0.3, avoids a two-dimensional exploration of the regularization parameter space. Note that this regularization scheme is similar to the scheme previously presented by Kelbert et al. (2008), who however defined the inverse of W.
3.3 Optimization method
To minimize the penalty function given in Eq. (13), we apply the limited-memory quasi-Newton method (LMQN). This method has become a popular tool to solve large 3-D EM inverse problems numerically (e.g. Haber, 2005; Avdeev and Avdeeva, 2009). Our implementation of the method follows Nocedal and Wright (2006). The iterative formula for updating the model vector m is

where H(k ) is an approximation to the inverse Hessian matrix, updated at every iteration k, using the limited-memory Broyden-Fletcher-Goldfarb-Shanno formula. The step length α(k) is computed by an inexact line search.
4. Model Studies
In order to test the performance of our inversion scheme, we generate synthetic data (i.e. time series of internal coefficients) in a test 3-D conductivity model, hereinafter referred to as “target model”, and afterwards recover this model from the data. We introduce the target conductivity model (Section 4.1), describe how we generate the test data (Section 4.2) and finally present the results of our model studies (Section 4.3).
4.1 Target conductivity model
Figure 1 shows the target conductivity model. It consists of a thin surface shell of laterally varying conductance and a layered model, which contains different conductivity anomalies, underneath. The shell conductance is obtained by considering contributions both from seawater and sediments. The conductance of seawater has been taken from Manoj et al. (2006) and accounts for ocean bathymetry, ocean salinity, temperature and pressure. Conductance of the sediments (in continental as well as oceanic regions) is based on the global sediment thicknesses given by Laske and Masters (1997) and calculated by a heuristic procedure similar to that described in Everett et al. (2003). The surface shell is scaled to a thickness of 10 km.
Three local conductors of 0.04 S/m, representing possible mantle plumes and subduction zones, are embedded in a resistive layer of 0.004 S/m that extends from 10 km to 400 km. A deep-seated large-scale structure with conductivity of 1 S/m, describing a hypothetical regional conductor beneath the Pacific plate, is embedded in a layer of 0.04 S/m that extends from 400 km to 700 km. At depths between 700 km and the core-mantle boundary at 2900 km, the target model consists of a uniform conductor of 2 S/m; a perfect conductor representing the core is prescribed beneath. Each spherical sub-layer is discretized laterally in 180 × 90 cells of 2° × 2°. Note that the aim of this model is not to mimic the “true” world, but to provide a test model for our retrieval algorithm.
4.2 Generation of the test data set
Hourly mean time series of external coefficients in a geomagnetic dipole coordinate system (up to degree n = 3 and order m = 1) have been obtained by analysis of 4.5 years of observatory data (July 1998–December 2002), details of the derivation are given in Olsen et al. (2006). These time series are depicted in Fig. 2. The procedure to obtain the time series of internal coefficients in large parts follows the general scheme described in Olsen and Kuvshinov (2004) and Kuvshinov and Olsen (2005). Here, we only summarize the key steps, a more extensive description is given in Kuvshinov et al. (2006).
Time series of the external coefficients  (in nT) that describe the source in our model study. The time (in days) is relative to January 1, 2000. Note that the real coefficients
(in nT) that describe the source in our model study. The time (in days) is relative to January 1, 2000. Note that the real coefficients  shown in this figure are related to the complex coefficients
shown in this figure are related to the complex coefficients  in the following way (cf. Kuvshinov et al., 2006):
in the following way (cf. Kuvshinov et al., 2006):  , and
, and  .
.
-
1)
Fourier transformation of the external coefficients
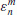 .
. -
2)
Simulation of EM induction by spherical harmonic sources
 , for a set of logarithmically spaced frequencies ω
j
, using a numerical solution (Kuvshinov, 2008) based on a contracting integral equation approach (Pankratov et al., 1995).
, for a set of logarithmically spaced frequencies ω
j
, using a numerical solution (Kuvshinov, 2008) based on a contracting integral equation approach (Pankratov et al., 1995). -
3)
For each frequency ω j , recovery of
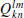 by spherical harmonic analysis of the simulated B
r
(k, l ≤ 15).
by spherical harmonic analysis of the simulated B
r
(k, l ≤ 15). -
4)
Spline interpolation of
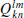 to all frequencies.
to all frequencies. -
5)
Calculation of the time spectra of internal coefficients
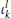 using Eq. (10).
using Eq. (10). -
6)
Inverse Fourier transformation of the recovered
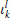 .
.
These data constitute a noise-free input for the 3-D inversion. For these noise-free data, the model covariance matrix C d is represented by the identity matrix. Results of such a test inversion are presented in Section 4.3.
In order to realistically simulate the full processing of Swarm data, we however use  and
and  to predict the mag-netospheric field at orbit altitudes and observatory locations (with a sampling frequency of 1 Hz). Adding the contributions due to different sources (core, lithosphere and ionosphere) yields the magnetic field at orbit altitudes and observatory locations, which is then analyzed by the CI (Sabaka et al., 2013). The external and internal SHE coefficients of the magnetic potential due to magnetospheric sources recovered by the CI constitute a realistic test data set for our inversion scheme. As mentioned in Section 2.2 (cf. Eq. (15)), we use a diagonal model covariance matrix C
d
, containing the squared uncertainties of the internal coefficients
to predict the mag-netospheric field at orbit altitudes and observatory locations (with a sampling frequency of 1 Hz). Adding the contributions due to different sources (core, lithosphere and ionosphere) yields the magnetic field at orbit altitudes and observatory locations, which is then analyzed by the CI (Sabaka et al., 2013). The external and internal SHE coefficients of the magnetic potential due to magnetospheric sources recovered by the CI constitute a realistic test data set for our inversion scheme. As mentioned in Section 2.2 (cf. Eq. (15)), we use a diagonal model covariance matrix C
d
, containing the squared uncertainties of the internal coefficients  , which are also recovered by the CI.
, which are also recovered by the CI.
4.3 Inversion results
Recovered time series of  and
and  are provided by the CI with a sampling rate of 6 hours. The noise-free data are also re-sampled to 6 hours, and internal coefficients with k > 5 are omitted in order to have structurally similar datasets. For each dataset, we perform a Fourier transformation of both external and internal coefficient time series and pick a subset of representative periods. Tests showed that optimum results are obtained for a period range between two days and two months. For the tests presented in this study, we used 20 logarithmically spaced periods in the above-mentioned range.
are provided by the CI with a sampling rate of 6 hours. The noise-free data are also re-sampled to 6 hours, and internal coefficients with k > 5 are omitted in order to have structurally similar datasets. For each dataset, we perform a Fourier transformation of both external and internal coefficient time series and pick a subset of representative periods. Tests showed that optimum results are obtained for a period range between two days and two months. For the tests presented in this study, we used 20 logarithmically spaced periods in the above-mentioned range.
We invert these data to recover the conductivity at depths between 10 km and 1000 km. The surface conductance map describing the distribution of land and sea is scaled to a thickness of 10 km and fixed, i.e. we do not try to recover it, as its contribution to the induced field is assumed to be known. The inversion domain consists of five layers, each having a thickness of 200 km (except for the uppermost layer, which has a thickness of 190 km). This stratification intentionally does not coincide with the stratification of the target model (cf. Section 4.1) in order to account for our limited knowledge of the stratification in Earth’s mantle.
For forward modelling, each layer (including the thin surface shell) is discretized in 72 × 36 cells of 5° × 5°. Since our data consist of internal coefficients of degree k ≤ 5, we also choose L = 5 as cut-off degree for the spherical harmonic representation of the conductivity in each layer. Although the maximum degrees of data and model are not strictly correlated, tests showed that higher L generate small-scale artefacts in the inversion results, but do not increase the resolution of the anomalous structures. As we use an iterative solver (cf. Section 3.3), an initial conductivity model is required. This model consists of the laterally heterogeneous surface shell and a 1-D section underneath, which has been derived from the data by a 1-D inversion algorithm (cf. companion paper by Püthe and Kuvshinov, 2013). The conductivity at depths greater than 1000 km is fixed in subsequent iterations just like the conductivity of the surface shell.
The inversion results are presented in Fig. 3. The first column shows the target model “filtered” by spherical harmonics up to degree 5, thereby representing the most detailed picture we can obtain for each layer with the implemented parameterization. Note that the small-scale anomalies in the upper mantle have disappeared, thus indicating that the resolution of our algorithm is limited to large-scale structures (i.e. structures of continental size).
First column: Target conductivity model filtered by spherical harmonics up to degree p = 5. Second column: Conductivity model recovered from noise-free data. Third column: Conductivity model recovered from data provided by the CI, using signals from all three satellites of the Swarm constellation and observatory measurements. Fourth column: Conductivity model recovered from data provided by the CI, using observatory measurements and signals from only those two satellites of the Swarm constellation that fly side-by-side (Swarm A and B). Note the different stratifications of target model and recovered model, especially in the overlap zone between 600 km and 800 km. Conductivities are in units of S/m.
The second column shows the conductivity structure recovered with noise-free data. The shape of the large-scale anomaly below the Pacific plate is recovered very well in the layer extending from 400 km to 600 km, and conductivities of both anomaly and background match with the filtered target model. The layers extending from 10 km to 200 km and from 200 km to 400 km coincide perfectly well with the (quasi-uniform) filtered target model in this depth range. The same is true for the layer extending from 800 km to 1000 km. The layer extending from 600 km to 800 km samples contributions of two layers of the target model (note the different stratifications). Its conductivity distribution appears very reasonable, since the background has an intermediate conductivity when compared to both layers of the filtered target model, and the Pacific plate anomaly is clearly visible.
The third column shows the conductivity structure recovered with realistic test data, i.e. data provided by the CI, generated by simulating observatory measurements and measurements of the three satellites of the Swarm mission in orbit. The shape of the Pacific plate anomaly is blurred when compared to the results obtained with noise-free data, but its conductivity (as well as the background conductivity) matches with the filtered target model. The recovery of the other layers is very similar to the noise-free case, except for the layer extending from 200 km to 400 km, in which a “ghost effect” of the large-scale anomaly is perceptible. This might indicate that the data in the considered period range contain only limited information on the conductivity at shallow depths.
As a “failure case study”, an additional run of the CI was performed using simulated observatory measurements and measurements of the two satellites of the Swarm mission that are supposed to fly side-by-side (Swarm A and B, cf. Friis-Christensen et al., 2006). Results are shown in the fourth column of Fig. 3. The recovery of the Pacific plate anomaly is comparable to the previous case with data from all three satellites. The recovered model however contains some artefacts in deeper regions. Since the two side-by-side flying satellites are equivalent to a single satellite for mantle conductivity studies, this result indicates that it is possible to obtain a good estimate of the 3-D mantle conductivity structure even with data from the global net of observatories and a single satellite, i.e. also from recent missions as, in particular, CHAMP.
The results presented in Fig. 3 were chosen out of a multitude of results obtained with different regularization parameters λ, cf. Eq. (13). The final result was gained by analysis of the trade-off curve (L-curve) relating data misfit ϕ d and regularization term ϕ s (Hansen, 1992). Figure 4 shows the L-curve for the inversion runs using the realistic data set (with data from all three satellites); the results shown in the third column of Fig. 3 correspond to the point for λ = 20 in the “knee” of the L-curve.
Trade-off curve relating data misfit ϕ d and regularization term ϕ s for the inversion runs using the realistic data set. The results for λ = 20 are depicted in the third column of Fig. 3.
5. Discussion and Conclusions
We have presented a 3-D frequency domain inversion scheme to invert satellite magnetic data for global mantle conductivity. The scheme is based on the analysis of time spectra of the internal (induced) coefficients of the SHE of the magnetic potential due to magnetospheric sources. The efficacy of the inversion is achieved by the implementation of a limited memory quasi-Newton method and the usage of an adjoint approach to calculate the misfit gradient. Par-allelization with respect to frequencies and an efficient implementation of the computation of Green’s tensors further accelerate the calculations. Producing the inversion results presented in this paper only took a few hours on 20 nodes of ETH’s cluster “Brutus”.
We parameterize our model domain in terms of spherical harmonics. This parameterization reflects the nature of the data and allows, compared to a block parameterization, a dramatic reduction of the number of model parameters. This stabilizes the solution, as additional tests have shown. The chosen basis does not permit the recovery of sudden lateral jumps in conductivity (sudden vertical jumps, which are expected to occur in the mantle transition zone, can however be mimicked). But in the considered depth range and due to the diffusive nature of electromagnetic fields, we cannot expect to resolve sudden jumps in conductivity anyway. On the other hand, the chosen parameterization diminishes the number of artefacts in the solution. Considering that with the expected data from Swarm, our algorithm can only resolve structures of continental scale, this advantage outweighs the drawbacks.
The algorithm has been tested by simulating induction due to a realistic magnetospheric source in a realistic 3-D conductivity model and recovering this model from the synthetic data. The data consist of internal SHE coefficients up to degree and order 5 at periods between two days and two months. By using noise-free data, an excellent recovery of the shape and conductivity of an anomalous large-scale structure at mid-mantle depths (400 km–700 km) has been shown to be possible, whereas the resolution of more detailed structures is limited by the available data. The conductivity of the anomalous structure could also be recovered very well with realistic data provided by the CI, though its shape is slightly blurred. The information in the data on conductivity at shallow depths appears to be limited. The good recovery of the target model with realistic test data in retrospect justifies our neglect of interdependencies between the experimental internal coefficients of different degrees and orders by using a diagonal data covariance matrix. We however plan to implement and investigate the use of the full data covariance matrix, which can be provided by the CI, before applying our formalism to real data.
The presented tests show that the inversion algorithm is workable and ready to digest Swarm data, and might even yield reliable estimates of the 3-D mantle conductivity structure with data from recent single satellite missions and the global net of geomagnetic observatories. Further efforts will thus concentrate on the development of a more flexible (modular) structure of the scheme, allowing e.g. the easy insertion of an alternative optimization scheme, such as non-linear conjugate gradients. This flexibility might allow the combination of the inversion scheme presented in this study with similar global inversion algorithms using observatory data (Semenov and Kuvshinov, 2012; Koch and Kuvshinov, 2013) and thus permit a more robust recovery of mantle conductivity, especially at shallow depths.
The development of an alternative 3-D inverse solution is currently in progress. This alternative scheme is not based on internal coefficients  , but on the transfer functions
, but on the transfer functions  , cf. Eq. (10), and thus independent of the source. Another advantage of this scheme is its applicability to patchy time series. The derivation of the elements of the Q-matrix by multivariate analysis and their inversion for mantle conductivity in a similar framework as presented above will be the topic of a forthcoming publication.
, cf. Eq. (10), and thus independent of the source. Another advantage of this scheme is its applicability to patchy time series. The derivation of the elements of the Q-matrix by multivariate analysis and their inversion for mantle conductivity in a similar framework as presented above will be the topic of a forthcoming publication.
References
Avdeev, D. and A. Avdeeva, 3D magnetotelluric inversion using a limited-memory quasi-Newton optimization, Geophysics, 74, 45–57, 2009.
Banks, R., Geomagnetic variations and the electrical conductivity of the upper mantle, Geophys. J. R. Astron. Soc, 17, 457–487, 1969.
Becker, T. and L. Boschi, A comparison of tomographic and geodynamic mantle models, Geochem. Geophys. Geosyst., 3, doi:10.129/2001GC000168, 2002.
Chulliat, A., X. Lalanne, L. R. Gaya-Peque, F. Truong, and J. Savary, The new Easter Island magnetic observatory, Pages 47-53 of: Love, J. (ed), Proceedings of the XIIIth IAGA workshop on geomagnetic observatory instruments, data acquisition and processing, 2009.
Constable, S. and C. Constable, Observing geomagnetic induction in magnetic satellite measurements and associated implications for mantle conductivity, Geochem. Geophys. Geosyst., 5, doi:10.1029/2003GC000634, 2004.
Dorn, O., H. Bertete-Aquirre, J. G. Berryman, and G. C. Papanicolaou, A nonlinear inversion method for 3D electromagnetic imaging using adjoint fields, Inverse Problems, 15, 1523–1558, 1999.
Everett, M. E., S. Constable, and C. G. Constable, Effects of near-surface conductance on global satellite induction responses, Geophys. J. Int., 153, 277–286, 2003.
Friis-Christensen, E., H. Lühr, and G. Hulot, Swarm: A constellation to study the Earth’s magnetic field, Earth Planets Space, 58 351–358, 2006.
Fukao, Y., T. Koyama, M. Obayashi, and H. Utada, Trans-Pacific temperature field in the mantle transition region derived from seismic and electromagnetic tomography, Earth Planet. Sci. Lett., 217, 425–434, 2004.
Haber, E., Quasi-Newton methods for large-scale electromagnetic inverse problems, Inverse Problems, 21, 305–323, 2005.
Hansen, P. C, Analysis of discrete ill-posed problems by means of the L-curve, SIAMRev., 34, 561–580, 1992.
Kelbert, A., G. Egbert, and A. Schultz, Non-linear conjugate gradient inversion for global EM induction: resolution studies, Geophys. J. Int., 173, 365–381, 2008.
Kelbert, A., A. Schultz, and G. Egbert, Global electromagnetic induction constraints on transition-zone water content variations, Nature, 460, 1003–1007, 2009.
Koch, S. and A. Kuvshinov, Global 3-D EM inversion of Sq variations based on simultaneous source and conductivity determination: concept validation and resolution studies, Geophys. J. Int., 195, 98–116, 2013.
Korte, M., M. Mandea, H. J. Linthe, A. Hemshorn, P. Kotze, and E. Ricaldi, New geomagnetic field observations in the South Atlantic Anomaly region, Ann. Geophys., 52, 65–82, 2009.
Koyama, T., A study on the electrical conductivity of the mantle by voltage measurements of submarine cables, Ph.D. thesis, University of Tokyo, 2001.
Koyama, T., H. Shimizu, H. Utada, M. Ichiki, E. Ohtani, and R. Hae, Water content in the mantle transition zone beneath the North Pacific derived from the electrical conductivity anomaly, in Earth’s Deep Water Cycle, edited by Jacobsen, S. and S. van der Lee, AGU Geophys. Monogr. Ser., vol. 168, 171–179, 2006.
Kuvshinov, A., 3-D Global induction in the oceans and solid Earth: recent progress in modeling magnetic and electric fields from sources of mag-netospheric, ionospheric and oceanic origin, Surv Geophys, 29, 139–186, 2008.
Kuvshinov, A., Deep electromagnetic studies from land, sea and space: Progress status in the past 10 years, Surv. Geophys., 33, 169–209, 2012.
Kuvshinov, A. and N. Olsen, Modelling the ocean effect of geomagnetic storms at ground and satellite altitude, in Earth Observation with CHAMP. Results from Three Years in Orbit, edited by Reigber, Ch., H. Lühr, P. Schwintzer, and J. Wickert, 353–358 Springer-Verlag, Berlin Heidelberg, 2005.
Kuvshinov, A. and N. Olsen, A global model of mantle conductivity derived from 5 years of CHAMP, Ørsted, and SAC-C magnetic data, Geophys. Res. Lett., 33, doi:10.1029/2006GL027083, 2006.
Kuvshinov, A. and A. Semenov, Global 3-D imaging of mantle electrical conductivity based on inversion of observatory C-responses I. An approach and its verification, Geophys. J. Int., 189, 1335–1352, 2012.
Kuvshinov, A., T. Sabaka, and N. Olsen, 3-D electromagnetic induction studies using the Swarm constellation: Mapping conductivity anomalies in the Earth’s mantle, Earth Planets Space, 58, 417–427, 2006.
Kuvshinov, A., J. Velímský, P. Tarits, A. Semenov, O. Pankratov, L. Tøffner-Clausen, Z. Martinec, N. Olsen, T. Sabaka, and A. Jackson, Level 2 products and performances for mantle studies withSwarm, Swarm Science Study under ESA contract, final report, 2010.
Laske, G. and G. Masters, A global digital map of sediment thickness, Eos Trans. AGU, 78, F483, 1997.
Manoj, C, A. Kuvshinov, S. Maus, and H. Lühr, Ocean circulation generated magnetic signals, Earth Planets Space, 58, 429–437, 2006.
Martinec, Z. and J. Velímský, The adjoint sensitivity method of EM induction for CHAMP magnetic data, Geophys. J. Int., 179, 1372–1396, 2009.
Matzka, J., N. Olsen, C. Fox Maule, L. Pedersen, A. Berarducci, and S. Macmillan, Geomagnetic observations on Tristan da Cuhna, South Atlantic Ocean, Ann. Geophys., 52, 97–105, 2009.
Nocedal, J. and S. Wright, Numerical Optimization, Springer-Verlag, Berlin Heidelberg, 2006.
Olsen, N. and A. Kuvshinov, Modeling the ocean effect of geomagnetic storms, Earth Planets Space, 56, 525–530, 2004.
Olsen, N., R. Haagmans, T. Sabaka, A. Kuvshinov, S. Maus, M. Purucker, M. Rother, V. Lesur, and M. Mandea, The Swarm End-To-End mission simulator study: Separation of the various contributions to Earth’s magnetic field using synthetic data, Earth Planets Space, 58,359–370,2006.
Pankratov, O. and A. Kuvshinov, General formalism for the efficient calculation of derivatives of EM frequency domain responses and derivatives of the misfit, Geophys. J. Int., 181, 229–249, 2010.
Pankratov, O., D. Avdeev, and A. Kuvshinov, Electromagnetic field scattering in a heterogeneous Earth: A solution to the forward problem, Phys. Solid Earth, 31, 201–209, 1995.
Püthe, C. and A. Kuvshinov, Determination of the 1-D distribution of electrical conductivity in Earth’s mantle from Swarm satellite data, Earth Planets Space, 65, this issue, 1233–1237, 2013.
Romanowicz, B., Global mantle tomography: progress status in the past 10 years, Ann. Rev. Earth Planet. Sci., 31, 303–328, 2003.
Sabaka, T. J., L. Tøffner-Clausen, and N. Olsen, Use of the Comprehensive Inversion method for Swarm satellite data analysis, Earth Planets Space, 65, this issue, 1201–1222, 2013.
Semenov, A. and A. Kuvshinov, Global 3-D imaging of mantle conductivity based on inversion of observatory C-responses C-responses. II, Data analysis and results, Geophys. J. Int., 191, 965–992, 2012.
Shimizu, H. and H. Utada, Ocean hemisphere geomagnetic network: its instrumental design and perspective for long-term geomagnetic observations in the Pacific, Earth Planets Space, 51, 917–932, 1999.
Shimizu, H., H. Utada, K. Baba, T. Koyama, M. Obayashi, and Y. Fukao, Three-dimensional imaging of electrical conductivity in the mantle transition zone beneath the North Pacific Ocean by a semi-global induction study, Phys. Earth Planet. Inter, 183, 262–269, 2010.
Tarits, P. and M. Mandea, The heterogeneous electrical conductivity structure of the lower mantle, Phys. Earth Planet. Inter., 183, 115–125,2010.
Toh, H., Y. Hamano, Y. Goto, and H. Utada, Long-term seafloor electromagnetic observation in the northwest Pacific may detect the vector geomagnetic secular variation, Data Sci. J., 9, IGY100-IGY109, 2010.
Utada, H., T. Koyama, M. Obayashi, and Y. Fukao, A joint interpretation of electromagnetic and seismic tomography models suggests the mantle transition zone below Europe is dry, Earth Planet. Sci. Lett., 281, 249–257, 2009.
Veíimský, J., Electrical conductivity in the lower mantle: Constraints from CHAMP satellite data by time-domain EM induction modeling, Phys. Earth Planet. Inter, 180, 111–117, 2010.
Veíimský, J., Determination of three-dimensional distribution of electrical conductivity in the Earth’s mantle from Swarm satellite data: Time-domain approach, Earth Planets Space, 65, this issue, 1239–1246,2013.
Velímský, J., Z. Martinec, and M. E. Everett, Electrical conductivity in the Earth’s mantle inferred from CHAMP satellite measurements. Data processing and 1-D inversion, Geophys. J. Int., 166, 529–542, 2006.
Acknowledgments
The authors thank Oleg Pankratov and Nils Olsen for discussions on different aspects of the paper. We also thank Mark Everett and an anonymous reviewer for helpful and constructive comments on the manuscript. This work has been supported by the European Space Agency through ESTEC contract No. 4000102140/10/NL/JA, by the Swiss National Science Foundation under grant No. 2000021-140711/1, and in part by the Russian Foundation for Basic Research under grant No. 12-05-00817-a.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Püthe, C., Kuvshinov, A. Determination of the 3-D distribution of electrical conductivity in Earth’s mantle from Swarm satellite data: Frequency domain approach based on inversion of induced coefficients. Earth Planet Sp 65, 1247–1256 (2013). https://doi.org/10.5047/eps.2013.09.004
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.5047/eps.2013.09.004


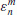 .
. , for a set of logarithmically spaced frequencies ω
j
, using a numerical solution (
, for a set of logarithmically spaced frequencies ω
j
, using a numerical solution (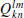 by spherical harmonic analysis of the simulated B
r
(k, l ≤ 15).
by spherical harmonic analysis of the simulated B
r
(k, l ≤ 15).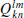 to all frequencies.
to all frequencies. using
using  .
.
