- Article
- Open access
- Published:
Geomagnetic secular variation violating the frozen-flux condition at the core surface
Earth, Planets and Space volume 62, pages 693–709 (2010)
Abstract
We consider a method to extract the part of a given geomagnetic secular variation (SV) model that is not consistent with a frozen-flux condition. This condition is usually derived from the diffusionless radial induction equation at the core-mantle boundary (CMB), and is defined explicitly in the spatial domain: radial flux changes within closed null-flux curves at the core surface are not allowed at any instant. We study here this condition in the spherical harmonic (SH) domain, relying on the SH expansion of the diffusionless equation. SV models at a certain epoch are separated into advective and non-advective parts. The advective (resp. non-advective) part satisfies (resp. does not satisfy) the frozen-flux condition redefined in the SH domain. We show that this separation is not unique. In this work, we achieve a unique separation by assuming the orthogonality of the two parts in terms of the radial SV energy at the CMB. From the recent geomagnetic models, GRIMM and CM4, we find that the non-advective part shows up mainly in the small reverse patches of the radial magnetic field at the CMB. However, non-advective behaviors are also observed outside these patches. As far as no restriction is imposed on core flow configuration, time variations of the non-advective part are not correlated to those of the SV models. However, if the flow is restricted to be tangentially geostrophic, time variations of the SV models have to be partly non-advective. Furthermore, for this flow configuration, the secular decrease of the axial dipole has to be largely non-advective.
1. Introduction
The temporal evolution of the Earth’s core field, generally known as main field (MF), occurs as a result of two different processes taking place in the electrically conducting fluid outer core: advection and diffusion. The advection allows the field to grow by converting kinetic energy of the core fluid flow into electromagnetic energy; the field is reorganized such that magnetic lines of force are fixed to the fluid material (frozen-flux (FF) theorem). The diffusion decays the field through Ohmic dissipation, and magnetic lines of force travel relatively to the material. The field evolution is described by the induction equation (Gubbins and Roberts, 1987)

where B is the magnetic field, v the flow velocity and ηc the magnetic diffusivity of the core fluid ( , with µ being the magnetic permeability of the free space and sc the electric conductivity of the core fluid). The overdot stands for the temporal derivative, and
, with µ being the magnetic permeability of the free space and sc the electric conductivity of the core fluid). The overdot stands for the temporal derivative, and  represents the geomagnetic secular variation (SV). The first and second terms on the right hand side (RHS) of the above equation correspond to the advection and diffusion, respectively.
represents the geomagnetic secular variation (SV). The first and second terms on the right hand side (RHS) of the above equation correspond to the advection and diffusion, respectively.
Timescales of these two processes vary with their spatial scales, the flow velocity and the conductivity. Their relative importance at a given timescale is measured by a set of these three parameters. On timescales from 1 year to some hundred years, typical parameter estimates for the Earth’s fluid core suggest that the observed field variation arises mostly from advective processes near the core surface (Roberts and Scott, 1965). Therefore, the outer core fluid may be reasonably considered as a perfect conductor, and the process generating field variations is described by the induction equation without the diffusion term. The radial component of the diffusionless equation at the spherical core surface (mean radius c = 3485.0 km) is then written as

The subscripts r and H denote the radial and horizontal components, respectively. The above equation describes the assumption that the decadal field variations  r at the core-mantle boundary (CMB) are totally attributed to the advection of the field Br by the horizontal core flow vH at the top of the core (we hereafter refer to it as ‘FF assumption’). This is indeed a good approximation of the decadal SV generation process, as long as its spatial scale is no less than ~ 103 km in both the radial and horizontal directions (Braginsky and Le Mouël, 1993).
r at the core-mantle boundary (CMB) are totally attributed to the advection of the field Br by the horizontal core flow vH at the top of the core (we hereafter refer to it as ‘FF assumption’). This is indeed a good approximation of the decadal SV generation process, as long as its spatial scale is no less than ~ 103 km in both the radial and horizontal directions (Braginsky and Le Mouël, 1993).
The assumption can be examined on the basis of geomagnetic field models downward continued to the core surface. Equation (1) leads to various necessary conditions (we hereafter refer to them as ‘FF conditions’) that have to be satisfied by radial MF and SV at the CMB (Backus, 1968). First, a set of surface integral conditions

can be deduced from Eq. (1) (Backus, 1968). These conditions require that, at every instant, no radial magnetic flux changes occur through every core surface patch Ci closed by a null-flux curve (contour of Br = 0 on the CMB). This condition, particularly referred to as the Backus’ FF condition hereafter, is only necessary and not sufficient for  r to be exclusively generated by advection (Gubbins, 1984). Combining the integrals for all Ci, one can also derive a single necessary condition
r to be exclusively generated by advection (Gubbins, 1984). Combining the integrals for all Ci, one can also derive a single necessary condition

where the integral is over the whole spherical surface of the core with the radius c. This condition describes temporal invariance of the ‘total unsigned flux’ F, or the total number of magnetic line of force across the CMB (Bondi and Gold, 1950; Holme and Olsen, 2006). The other useful form of the necessary condition is obtained by time-integrating Eq. (2) for each Ci. It then follows that, under the temporally continuous FF assumption, magnetic flux for each Ci must be conserved in time. This condition has been used to test magnetic models, showing that they are not consistent with the FF assumption (Bloxham and Gubbins, 1985).
If a given SV model contains elements violating the above conditions, they must be attributed to either or both of two other possible origins. First, the modelled SV at large spatial scales can result from the advection of unmodelled MF at small spatial scales (Eymin and Hulot, 2005; Pais and Jault, 2008). The second origin is diffusion. It has been argued that this is possibly associated with a phenomenon often referred to as flux expulsion, which arises from toroidal field and upwelling core flow below the CMB (Bloxham, 1986; Gubbins, 1996, 2007). The diffusion can even be important for the quasi-steady part of the SV at large scales in space (Love, 1999).
In this study, we propose a method to specify the part of a SV model inconsistent with the FF condition. The method is applied to given magnetic field models for recent years. We do not intend to provide a test of the FF condition, but rather probe the spatial distribution, and time evolution, of a possible diffusion contribution to the model. Indeed, it seems very difficult to perform a conclusive test against the condition, as magnetic models mapped at the CMB are subject to considerable ambiguity. Their morphology at the CMB always has errors due to model variances and truncation of unresolvable components. In particular, both MF and SV models have spectra at the CMB that do not converge, and the integral conditions are sensitive to the truncation level (Holme and Olsen, 2006). Despite this difficulty, there is practically no other way to assess the FF assumption than using or building truncated field models (Gubbins, 1984; Bloxham and Gubbins, 1986; Benton and Celaya, 1991; Constable et al., 1993; O’Brien et al., 1997; Whaler and Holme, 2007; Jackson et al., 2007). Here, we also start with existing truncated field models to extract a SV part not satisfying the FF condition. Again we stress that this part is unexplained by the advection associated with the MF and core flow below their truncation levels. It can still result from the advection associated with the unmodelled MF and core flow at small scales.
Instead of the spatial domain approach investigating the SV flux through each Ci, we adopt a spherical harmonic (SH) domain approach to assess SV models. An expression corresponding to Eq. (1) can be derived in SH domain by expanding the relevant quantities Br,  r and vH (all defined on the spherical surface of the CMB) in a truncated series of the spherical harmonics. The obtained equations are the observation equations often used in estimating core flow models based on magnetic models (Bloxham and Jackson, 1991; Holme, 2007). By making use of these equations, one may be able to find the part of the SV which cannot be related to the core flow for a given truncated MF. This approach requires only an algebraic procedure, without any geometric concern about the domain of integration, such as the null-flux patches Ci. Moreover, the FF condition redefined in the SH domain is likely to be stronger than the Backus’ FF condition, as it turns out in this study. Another technical advantage of the SH domain approach is the facility to incorporate assumptions needed for treating the non-uniqueness issue, when separating the SV parts satisfying and not satisfying the FF condition. We thus consider the SH domain approach worth an investigation, particularly when dealing with magnetic models given in SH coefficients.
r and vH (all defined on the spherical surface of the CMB) in a truncated series of the spherical harmonics. The obtained equations are the observation equations often used in estimating core flow models based on magnetic models (Bloxham and Jackson, 1991; Holme, 2007). By making use of these equations, one may be able to find the part of the SV which cannot be related to the core flow for a given truncated MF. This approach requires only an algebraic procedure, without any geometric concern about the domain of integration, such as the null-flux patches Ci. Moreover, the FF condition redefined in the SH domain is likely to be stronger than the Backus’ FF condition, as it turns out in this study. Another technical advantage of the SH domain approach is the facility to incorporate assumptions needed for treating the non-uniqueness issue, when separating the SV parts satisfying and not satisfying the FF condition. We thus consider the SH domain approach worth an investigation, particularly when dealing with magnetic models given in SH coefficients.
It is also of interest, while easy to perform in the SH domain, to extend the condition so as to incorporate a further condition derived from tangential geostrophy (TG) assumption. This assumption restricts the flow vH only to those in horizontal geostrophic balance (Le Mouël, 1984). The TG flow vH satisfies a constraint

all over the core surface, where θ is the colatitude. The TG assumption has been considered plausible for the Earth’s core surface flow, and often adopted in the flow inversions, either strictly (e.g. Gire and Le Mouël, 1990; Jackson, 1997; Le Huy et al., 2000) or with a small relaxation (Pais et al., 2004). In this paper, we refer to the combined condition of the FF and the strict TG as the ‘FF+TG condition’. Especially, we refer to the integral condition in the spatial domain given by Chulliat and Hulot (2001) as CH’s FF+TG condition. The vorticity constraint, which holds when the mantle is electrically insulating (Gubbins, 1991), is deduced from the CH’s FF+TG condition. It has already been shown that a magnetic model compatible with the FF condition and vorticity constraint can be derived (Jackson et al., 2007). Yet, the compatibility of a given magnetic model with the CH’S FF+TG condition has not been studied with the aim to assess the TG assumption. The SV violating the FF+TG condition can be attributed to either the advection due to the ageostrophic flow (Hulot and Chulliat, 2003) or the diffusion. It can also arise from the advection associated with the unmodelled MF and the TG flow at small scales, when truncated models are considered.
In the next section we introduce the advective and non-advective SV parts and then the essential non-uniqueness of decomposing a given SV into these parts. In Section 3 we outline the SH domain expression of the FF induction equation (1) and describe our method to specify each SV part. We present the magnetic models to be examined in Section 4, and the computation results in Section 5. Geophysical interpretation of the results are discussed in Section 6, and conclusions follow in the last section.
2. Advective and Non-advective SV Contributions and Non-uniqueness of Their Separation
Let us first define the advective and non-advective parts of a given model of the SV  o. Here, the MF model Bo as well as its time variation
o. Here, the MF model Bo as well as its time variation  o are estimated from observations above the Earth’s surface, with its mean radius a = 6371.2 km. We assume that the mantle behaves as an electric insulator on the timescales of decades and longer (Mandea Alexandrescu et al., 1999; Pinheiro and Jackson, 2008); then the models Bo and
o are estimated from observations above the Earth’s surface, with its mean radius a = 6371.2 km. We assume that the mantle behaves as an electric insulator on the timescales of decades and longer (Mandea Alexandrescu et al., 1999; Pinheiro and Jackson, 2008); then the models Bo and  o can be downward continued through the mantle to the CMB, corresponding by one-to-one to distributions of the radial MF, (Bo)r, and the radial SV, (
o can be downward continued through the mantle to the CMB, corresponding by one-to-one to distributions of the radial MF, (Bo)r, and the radial SV, ( o)r over the CMB (r = c), respectively. The part of
o)r over the CMB (r = c), respectively. The part of  o which can result from the core flow vH through Eq. (1) for a given (Bo)r is referred to as ‘advective SV’, and we denote it by
o which can result from the core flow vH through Eq. (1) for a given (Bo)r is referred to as ‘advective SV’, and we denote it by  ad. The radial advective SV, (
ad. The radial advective SV, ( ad)r, at the CMB necessarily satisfies the Backus’ FF condition (2). On the contrary, the SV part,
ad)r, at the CMB necessarily satisfies the Backus’ FF condition (2). On the contrary, the SV part,  na, which does not satisfy the condition (2) and hence cannot be attributed to the advection is referred to as ‘non-advective SV’. We consider that a given SV model
na, which does not satisfy the condition (2) and hence cannot be attributed to the advection is referred to as ‘non-advective SV’. We consider that a given SV model  o consists of these two SV parts,
o consists of these two SV parts,  o =
o =  ad +
ad +  na, above the CMB. A similar partition of
na, above the CMB. A similar partition of  o can be made when the core flow vH is limited to the strict TG flow satisfying the constraint (4). The SV parts,
o can be made when the core flow vH is limited to the strict TG flow satisfying the constraint (4). The SV parts,  ge and
ge and  ng, which can and cannot be generated by the TG flow through Eq. (1) are designated as ‘geostrophic SV’ and ‘non-geostrophic SV’, respectively. The FF+TG condition is thus necessarily met only by the geostrophic SV. The given SV model above the CMB is expressed as
ng, which can and cannot be generated by the TG flow through Eq. (1) are designated as ‘geostrophic SV’ and ‘non-geostrophic SV’, respectively. The FF+TG condition is thus necessarily met only by the geostrophic SV. The given SV model above the CMB is expressed as  o =
o =  ge +
ge +  ng as well. See Table 1 for the summary of the notations introduced here.
ng as well. See Table 1 for the summary of the notations introduced here.
The above decompositions of  o are not unique. There are necessary conditions only, but no sufficient conditions for
o are not unique. There are necessary conditions only, but no sufficient conditions for  o to be
o to be  ad or
ad or  ge. On the other hand, there are only sufficient conditions (i.e. violating the FF or FF+TG condition), but no necessary conditions for
ge. On the other hand, there are only sufficient conditions (i.e. violating the FF or FF+TG condition), but no necessary conditions for  o to be
o to be  na or
na or  ng. It follows that one can always have another decomposition, for example,
ng. It follows that one can always have another decomposition, for example,  , where
, where  and
and  , with being an arbitrary advective SV. It is even possible that
, with being an arbitrary advective SV. It is even possible that  o is totally due to
o is totally due to  na or
na or  ng.
ng.
A criterion is required to extract  na or
na or  ng uniquely from
ng uniquely from  o. This can be provided by defining a scalar product
o. This can be provided by defining a scalar product  of two potential fields, and the associated norm
of two potential fields, and the associated norm  . Then one can uniquely separate into two parts
. Then one can uniquely separate into two parts  ad and
ad and  na, or
na, or  ge and
ge and  ng, such that
ng, such that
-
1)
they are orthogonal with regard to the scalar product:
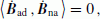 (5)
(5) (6)
(6) -
2)
the square norm
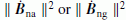 is minimum.
is minimum.
The criterion given by Eq. (5) (resp. Eq. (6)) thus equalizes the square norm of  o and the sum of those of
o and the sum of those of  ad and
ad and  na (resp.
na (resp.  ge and
ge and  ng), i.e.
ng), i.e.  (resp.
(resp.  ).
).
For the definition of the scalar product, we select here

( 1 and
1 and  2 are arbitrary potential SVs for r = c). The square norm
2 are arbitrary potential SVs for r = c). The square norm  then represents the energy of the radial SV,
then represents the energy of the radial SV,  , integrated over the CMB. We thus specify
, integrated over the CMB. We thus specify  na (resp.
na (resp.  ng) whose radial component (
ng) whose radial component ( na)r (resp. (
na)r (resp. ( ng)r)at the CMB has minimum energy and simultaneously makes no energy cancellation with (
ng)r)at the CMB has minimum energy and simultaneously makes no energy cancellation with ( ad)r (resp. (
ad)r (resp. ( ge)r). In the core, however, it is possible that the diffusion and advection cancel each other to a certain extent in generating the SV. In this case, the scalar products in Eqs. (5) and (6) are not zero. Voorhies (1993) suggests that these products are likely to be negative. It is unknown, however, to what extent this cancellation occurs. Here, we simply regard
ge)r). In the core, however, it is possible that the diffusion and advection cancel each other to a certain extent in generating the SV. In this case, the scalar products in Eqs. (5) and (6) are not zero. Voorhies (1993) suggests that these products are likely to be negative. It is unknown, however, to what extent this cancellation occurs. Here, we simply regard  na or
na or  ng obtained this way as the smallest SV part, possibly due to the non-advective contribution.
ng obtained this way as the smallest SV part, possibly due to the non-advective contribution.
The definitions of the SV parts, the non-uniqueness issue and the orthogonal decomposition are made even clearer by introducing a linear space of the general potential SV and its linear subsets (see Appendix A).
3. SH Domain Approach
In this section we describe our method to extract the non-advective or non-geostrophic SV for certain MF and SV models given at a certain epoch. In the SH domain, we find  na by making an algebraic analysis of the FF induction equation expanded in spherical harmonics. A modification of this equation allows us to find
na by making an algebraic analysis of the FF induction equation expanded in spherical harmonics. A modification of this equation allows us to find  ng in the same way.
ng in the same way.
3.1 FF induction equation in the SH domain
Models of the MF and SV are usually represented in terms of the Gauss coefficients (MF and SV coefficients) truncated at certain degrees. Let LMF and LSV denote their truncation degrees, respectively. Because of the assumption of the insulating mantle, their radial components, Br and  r, at the CMB can be written as a linear combination of these Gauss coefficients. Also, the core flow vH is parameterized with the SH coefficients of the toroidal and poloidal scalars defined on the spherical surface of the CMB (Bloxham and Jackson, I99I). Then, the truncated expression of Eq. (1) in the SH domain can be written as the SH domain,
r, at the CMB can be written as a linear combination of these Gauss coefficients. Also, the core flow vH is parameterized with the SH coefficients of the toroidal and poloidal scalars defined on the spherical surface of the CMB (Bloxham and Jackson, I99I). Then, the truncated expression of Eq. (1) in the SH domain can be written as the SH domain,  , may become identical to that in the spatial domain,
, may become identical to that in the spatial domain,  , defined by Eq. (7), i.e.
, defined by Eq. (7), i.e.

where  (with the superscript T denoting the transpose) are the column vectors of the Gauss coefficients for SV. Elements of the matrix A are linear functions of the Gauss coefficients for MF
(with the superscript T denoting the transpose) are the column vectors of the Gauss coefficients for SV. Elements of the matrix A are linear functions of the Gauss coefficients for MF  , and m is the vector of the flow coefficients (Bloxham, 1988). According to the selection rule of the Gaunt and Elsasser integrals in A (Moon, 1979), the highest degree of the flow that can interact with MF in generating SV up to SH degree LMF is LFL = 2LMF. Then, the SV on the left hand side of Eq. (8) has possibly non-zero coefficients up to degree LSV = 3LMF (= LFL + LMF).For a given number of MF coefficients, NMF (= LMF(LMF + 2)), Eq. (8) has the coefficient vectors, m and
, and m is the vector of the flow coefficients (Bloxham, 1988). According to the selection rule of the Gaunt and Elsasser integrals in A (Moon, 1979), the highest degree of the flow that can interact with MF in generating SV up to SH degree LMF is LFL = 2LMF. Then, the SV on the left hand side of Eq. (8) has possibly non-zero coefficients up to degree LSV = 3LMF (= LFL + LMF).For a given number of MF coefficients, NMF (= LMF(LMF + 2)), Eq. (8) has the coefficient vectors, m and  , with their dimensions NFL (= 2LFL(LFL + 2) = 8LMF(LMF + 1)) and NSV (= LSV(LSV + 2) = 3LMF(3LMF + 2)), respectively (Table 2). Note that NSV> NFL for LMF > 2.
, with their dimensions NFL (= 2LFL(LFL + 2) = 8LMF(LMF + 1)) and NSV (= LSV(LSV + 2) = 3LMF(3LMF + 2)), respectively (Table 2). Note that NSV> NFL for LMF > 2.
 .
.The TG assumption can easily be incorporated into Eq. (1) in the SH domain. The TG flow is represented by a combination of the toroidal and poloidal flow basis functions, or the TG basis (Backus and Le Mouël, 1986). The vector w of TG flow coefficients is then related to m as m = Qw, where Q is the matrix with its elements described in Gire and Le Mouël (1990). Substituting this relation into Eq. (8) yields

where Atg = AQ. The dimension of w is reduced to  . In the case with the flow truncation degree LFL = 2LMF, Eq. (9) should have
. In the case with the flow truncation degree LFL = 2LMF, Eq. (9) should have  TG flow coefficients (Table 2). Note that
TG flow coefficients (Table 2). Note that  for any LMF > 0. In order to take criteria (5) and (6) into consideration, we renormalize the SV coefficients as
for any LMF > 0. In order to take criteria (5) and (6) into consideration, we renormalize the SV coefficients as  . The change-of-basis matrix W1/2 is selected so that the scalar product in
. The change-of-basis matrix W1/2 is selected so that the scalar product in

with l denoting the SH degree. Equations (8) and (9) are transformed respectively as  , where
, where  . The choice of the weight Eq. (10) corresponds to the choice of the scalar product (Eq. (7)). Indeed, a different choice of scalar product is associated with a different weight, leading ultimately to a different decomposition into advective and non-advective SVs. As described in the next subsection, the renormalized equations are indeed useful for the orthogonal decomposition with respect to our preferred definition of
. The choice of the weight Eq. (10) corresponds to the choice of the scalar product (Eq. (7)). Indeed, a different choice of scalar product is associated with a different weight, leading ultimately to a different decomposition into advective and non-advective SVs. As described in the next subsection, the renormalized equations are indeed useful for the orthogonal decomposition with respect to our preferred definition of  given by Eq. (7). In the remaining of this paper, the symbol tilde (˜) is omitted, whereas the SV coefficient vectors and matrices are all based on the modified basis, unless otherwise noted.
given by Eq. (7). In the remaining of this paper, the symbol tilde (˜) is omitted, whereas the SV coefficient vectors and matrices are all based on the modified basis, unless otherwise noted.
3.2 Specifying the non-advective and non-geostrophic SVs
The FF and FF+TG conditions in the SH domain are not directly linked to the usual integral conditions in the spatial domain (the Backus’ FF condition or CH’s FF+TG condition). Here, we derive the FF condition by analyzing the matrix A. A singular value decomposition of A is given by

where U and V are the orthogonal matrices with their dimensions NSV and NFL, respectively. A is the diagonal matrix of the singular values of A with its dimension NSV × NFL. We order these values  such that
such that  . The set of orthonormal column vectors uj (j = 1, ···, NSV) constituting
. The set of orthonormal column vectors uj (j = 1, ···, NSV) constituting  (i.e.
(i.e.  ] and
] and  forms a complete basis for an arbitrary SV coefficient vector
forms a complete basis for an arbitrary SV coefficient vector  . Hence, it is expanded uniquely as
. Hence, it is expanded uniquely as  . The scalar coefficients ßj are obtained by
. The scalar coefficients ßj are obtained by  . Similarly, a flow coefficient vector m is expanded as
. Similarly, a flow coefficient vector m is expanded as  , where Vi is the orthonormal column vector of dimension NFL constituting V (i.e.
, where Vi is the orthonormal column vector of dimension NFL constituting V (i.e.  and
and  ). The scalar coefficients aj are obtained by
). The scalar coefficients aj are obtained by  m. Substituting these expansions into
m. Substituting these expansions into  : = Am yields a set of scalar relations ßj = λjaj for j = 1, ..., NFL. If p (1 = p = NFL) is the rank of A, i.e. the largest value of j for which λj is non-zero (λj λ 0 only for 1 = j = p), the bases uj for j = 1, ... , p (resp. uj for j = p + 1, ..., NSV) represent the SV elements related (resp. not related) to m. We 697 refer to uj for j = p + 1, ... , NSV as the null-space SV eigenvectors. Now we can state the FF condition in the SH domain: it is necessary for the advective SV to be independent from all of the null-space SV eigenvectors. On the other hand, it is sufficient for the non-advective SV to be dependent on at least one of the null-space SV eigenvectors. The FF condition in the SH domain does not allow a unique separation of a given SV into the advective and non-advective parts. All of the components of the null-space SV eigenvectors have to be assigned to the non-advective part, but the rest of the components can be assigned to either part. Taking into account the criteria raised in Section 2 for a unique separation, we analyze the input models of MF, Bo, and SV,
: = Am yields a set of scalar relations ßj = λjaj for j = 1, ..., NFL. If p (1 = p = NFL) is the rank of A, i.e. the largest value of j for which λj is non-zero (λj λ 0 only for 1 = j = p), the bases uj for j = 1, ... , p (resp. uj for j = p + 1, ..., NSV) represent the SV elements related (resp. not related) to m. We 697 refer to uj for j = p + 1, ... , NSV as the null-space SV eigenvectors. Now we can state the FF condition in the SH domain: it is necessary for the advective SV to be independent from all of the null-space SV eigenvectors. On the other hand, it is sufficient for the non-advective SV to be dependent on at least one of the null-space SV eigenvectors. The FF condition in the SH domain does not allow a unique separation of a given SV into the advective and non-advective parts. All of the components of the null-space SV eigenvectors have to be assigned to the non-advective part, but the rest of the components can be assigned to either part. Taking into account the criteria raised in Section 2 for a unique separation, we analyze the input models of MF, Bo, and SV,  o, with their coefficient vectors denoted by bo and
o, with their coefficient vectors denoted by bo and  o, respectively. While
o, respectively. While  o itself is an NSV-dimensional vector, we allow it here to have non-zero SV coefficients only up to degree LMF for the sake of its consistency, with bo evolving in time. Let
o itself is an NSV-dimensional vector, we allow it here to have non-zero SV coefficients only up to degree LMF for the sake of its consistency, with bo evolving in time. Let  ad and
ad and  na denote the NSV-dimensional coefficient vectors of
na denote the NSV-dimensional coefficient vectors of  ad and
ad and  na, respectively. Then the decomposition
na, respectively. Then the decomposition  o =
o =  ad +
ad +  na is given by
na is given by  o =
o =  ad +
ad +  na in the SH domain. We obtain
na in the SH domain. We obtain  ad and
ad and  na uniquely by minimizing the square norm
na uniquely by minimizing the square norm  , yielding the SV parts
, yielding the SV parts

where  . Here, the non-advective SV
. Here, the non-advective SV  na consists exclusively of components of the null-space SV eigenvectors. Thus, once both bo and
na consists exclusively of components of the null-space SV eigenvectors. Thus, once both bo and  o are given at a certain epoch, the non-advective SV coefficients
o are given at a certain epoch, the non-advective SV coefficients  na can always be determined, whatever the flow is like. Note that this procedure enables the isolation of
na can always be determined, whatever the flow is like. Note that this procedure enables the isolation of  na while ensuring the criterion (5). Indeed, the orthonormality of uj allows the orthogonality
na while ensuring the criterion (5). Indeed, the orthonormality of uj allows the orthogonality  , which is equivalent to the criterion (5). The square norm of
, which is equivalent to the criterion (5). The square norm of  na is given by
na is given by  . The decomposition
. The decomposition  in the SH domain) under the criterion (6) can be made with the same procedure described above, but with Atg (with the dimension
in the SH domain) under the criterion (6) can be made with the same procedure described above, but with Atg (with the dimension  ) in place of A (with the dimension NSV × NFL). The process of finding
) in place of A (with the dimension NSV × NFL). The process of finding  na and
na and  ng described in this section is a practical implementation of the projection of a given SV onto its specific subspaces (see Appendix A).
ng described in this section is a practical implementation of the projection of a given SV onto its specific subspaces (see Appendix A).
4. Core Field Models
We use GRIMM (Lesur et al., 2008) and CM4 (Sabaka et al., 2004) as the input field models providing the coefficients bo and  o. These recent field models deserve to be investigated, as we believe that they achieve a very high accuracy, particularly in depicting the core field and its time variation. The FF condition is not imposed on either of the two models through their construction. They are both continuous in time, expanded in B-spline function, though with a different order and knot interval of the interpolating functions. One can derive snapshots of MF and SV at any epoch within their supporting time periods.
o. These recent field models deserve to be investigated, as we believe that they achieve a very high accuracy, particularly in depicting the core field and its time variation. The FF condition is not imposed on either of the two models through their construction. They are both continuous in time, expanded in B-spline function, though with a different order and knot interval of the interpolating functions. One can derive snapshots of MF and SV at any epoch within their supporting time periods.
GRIMM is a model constructed with vector magnetic data from the satellite CHAMP and ground-based observatories for the period 2001.0–2006.8. For the present study, we restrict the analysis to the period 2002.0–2005.0 in order to avoid the edge parts of this model, as they can be subject to degraded robustness. The short time span does not necessarily matter, because the test is done epoch by epoch against the FF condition using snapshots of MF and SV. Even for that short duration, the model seems to show remarkable variations, possibly regarded as geomagnetic jerks. It provides SV coefficients up to degree 14, but we consider them reliable only up to SH degree 12. The SV coefficients at degrees 13 and 14 have excessive powers with reference to the trend of the SV power spectrum, and are possibly contaminated by considerable noise. Therefore, we take LMF= 12 as the truncation degree of input models of MF and SV from GRIMM.
The comprehensive model CM4 is a model for a longer period, 1960.0–2002.0. This model is estimated using magnetic data primarily from ground-based observatories, supplemented by satellite measurements. Its accuracy may not compare with that of GRIMM due to the limited quantity and quality of data, but it features the well-known geomagnetic jerks which occurred succesively around the years 1969, 1978, 1991 and 1999 (Sabaka et al., 2004; Chambodut and Mandea, 2005). In our analysis we pay particular attention to the jerks, because we think of these abrupt events as special among all other SVs with respect that they are the core’s magnetic signals observed at the shortest timescale. The core field of CM4 is represented by its coefficients up to degree 14. Unlike GRIMM, the SV model of CM4 is damped at higher degrees. Yet, we take LMF= 13 as the truncation degree of input models of MF and SV from CM4, as the MF model may be affected by the lithospheric contribution at degree 14.
In Table 2, the dimensions of the matrices A and Atg are listed for both GRIMM and CM4 models.
5. Results
In this section, after the singular values of the matrices A and Atg, we present the non-advective and non-geostrophic SVs actually computed with our method. These two SV parts are extracted for the same epochs, at intervals of 0.5 year for GRIMM (2002.0–2005.0) and 1.0 year for CM4 (1960.0–2002.0).
5.1 Non-advective SV
The singular values λj of A for GRIMM at 2003.5 and CM4 at 1980.0 are shown in Fig. 1. We plot only the non-zero singular values λj for j = rank(A) = NFL - NO, where NO is the degree of freedom of the flow and equal to (LMF + 1)2. In the present analysis, we are not so much interested in the trend of λj with j. Instead, it is required to make sure whether these singular values λj(j = NFL - N0) are significantly different from zero in order to appropriately determine the value of p. For this purpose, the variances  of λj due to those of the input MF coefficients bo are estimated. The derivation of
of λj due to those of the input MF coefficients bo are estimated. The derivation of  from the covariance matrix
from the covariance matrix  of bo is described in Appendix B. Here,
of bo is described in Appendix B. Here,  is assumed to be diagonal. Its elements are given by
is assumed to be diagonal. Its elements are given by  , where ∆P (l) is the difference between the powers of two MF models at degree l. As the MF spectra of GRIMM and xCHAOS (Olsen and Mandea, 2008) show the difference somewhat independent of the degree l (Lesur et al., 2008), we let ∆P (l) = 1.0 [nT2] in the computation of
, where ∆P (l) is the difference between the powers of two MF models at degree l. As the MF spectra of GRIMM and xCHAOS (Olsen and Mandea, 2008) show the difference somewhat independent of the degree l (Lesur et al., 2008), we let ∆P (l) = 1.0 [nT2] in the computation of  for GRIMM. Similarly, we let ∆P(l) = 5.0 [nT2] for CM4; this is an ad hoc choice, considering the data set for CM4 as described in Section 4. We find that λj are all significantly greater than the computed singular value errors
for GRIMM. Similarly, we let ∆P(l) = 5.0 [nT2] for CM4; this is an ad hoc choice, considering the data set for CM4 as described in Section 4. We find that λj are all significantly greater than the computed singular value errors  (Fig. 1) and, hence, that they are significantly different from zero. This is confirmed with regard to any of the other epochs for bo from both GRIMM and CM4. We thus let p = NFL - N0 for calculating the non-advective SV (Eq. (11)).
(Fig. 1) and, hence, that they are significantly different from zero. This is confirmed with regard to any of the other epochs for bo from both GRIMM and CM4. We thus let p = NFL - N0 for calculating the non-advective SV (Eq. (11)).
Figure 2 illustrates the snapshots of ( o)r and (
o)r and ( na)r at the CMB for GRIMM at 2003.5 and CM4 at 1980.0. The maps of (
na)r at the CMB for GRIMM at 2003.5 and CM4 at 1980.0. The maps of ( na)r have features with spatial scales smaller than those of (
na)r have features with spatial scales smaller than those of ( o)r, as
o)r, as  na has non-zero coefficients up to the degree LSV, three times as high as the truncation degree LMF of
na has non-zero coefficients up to the degree LSV, three times as high as the truncation degree LMF of  o. Of course, from observational point of view, there is no resolution of SVs on such small scales and hence no point to discussing them. Therefore, we limit ourselves to arguing the location and intensity of the outstanding (
o. Of course, from observational point of view, there is no resolution of SVs on such small scales and hence no point to discussing them. Therefore, we limit ourselves to arguing the location and intensity of the outstanding ( na)r spots. This limitation also applies to the spatial domain studies (e.g. Jackson et al. (2007) use 812 gridding points on the CMB, which are beyond the SV resolution). As is expected from the FF condition, (
na)r spots. This limitation also applies to the spatial domain studies (e.g. Jackson et al. (2007) use 812 gridding points on the CMB, which are beyond the SV resolution). As is expected from the FF condition, ( na)r is apparently pronounced in some of the patches Ci, with single signed flux density changes over each of them. For example, (
na)r is apparently pronounced in some of the patches Ci, with single signed flux density changes over each of them. For example, ( na)r from both models in Fig. 2 is predominantly negative within the smaller reverse patch below the South Atlantic, nearby the Brazilic coast. (
na)r from both models in Fig. 2 is predominantly negative within the smaller reverse patch below the South Atlantic, nearby the Brazilic coast. ( o)r and (
o)r and ( na)r integrated over each Ci are of course the same because their difference (
na)r integrated over each Ci are of course the same because their difference ( o)r - (
o)r - ( na)r, which is equal to (
na)r, which is equal to ( ad)r, satisfies the FF condition (2).
ad)r, satisfies the FF condition (2).
A rather complex configuration of ( na)r is also seen in these results. We find the flux density changes with inhomogeneous distribution, or even with different signs within single patches covering a large area. For example, the maps of (
na)r is also seen in these results. We find the flux density changes with inhomogeneous distribution, or even with different signs within single patches covering a large area. For example, the maps of ( na)r for both GRIMM and CM4 indicate that the northern hemispheric patch has an outstanding area of non-zero (
na)r for both GRIMM and CM4 indicate that the northern hemispheric patch has an outstanding area of non-zero ( na)r localized below Indonesia, where the equatorial null-flux curve is particularly winding. This could not be revealed by allowing for the Backus’ FF condition. It is seen here because the FF condition used in the present work is stronger. It reduces the degree of freedom of B..
na)r localized below Indonesia, where the equatorial null-flux curve is particularly winding. This could not be revealed by allowing for the Backus’ FF condition. It is seen here because the FF condition used in the present work is stronger. It reduces the degree of freedom of B.. ad by NSV - p = 288, while the Backus’ FF condition by
ad by NSV - p = 288, while the Backus’ FF condition by  where
where  is the number of the null-flux patches Ci (the numbers are for the case with GRIMM at 2003.5). No matter what the flow configuration is (up to degree LFL), (
is the number of the null-flux patches Ci (the numbers are for the case with GRIMM at 2003.5). No matter what the flow configuration is (up to degree LFL), ( o)r in the winding null-flux curve below Indonesia cannot be attributed to the advection of the given MF model, though the curve is not locally closed to give a particular integral condition. In fact, the actual flow models have a difficulty in explaining downward continued SV models in this specific region, even if they are consistent with SV observations above the Earth’s surface (Wardinski et al., 2008). The computed (
o)r in the winding null-flux curve below Indonesia cannot be attributed to the advection of the given MF model, though the curve is not locally closed to give a particular integral condition. In fact, the actual flow models have a difficulty in explaining downward continued SV models in this specific region, even if they are consistent with SV observations above the Earth’s surface (Wardinski et al., 2008). The computed ( na)r thus implies that SV models can possibly contain non-advective spots at the CMB which do not violate the Backus’ FF condition (2) locally, in addition to those identified as simple flux density changes within the smaller reverse patches.
na)r thus implies that SV models can possibly contain non-advective spots at the CMB which do not violate the Backus’ FF condition (2) locally, in addition to those identified as simple flux density changes within the smaller reverse patches.
Comparing the time series of  o and
o and  na, we notice that their evolutions do not seem to be well correlated. In fact,
na, we notice that their evolutions do not seem to be well correlated. In fact,  na tends to show no sign of geomagnetic jerks, which are seen in
na tends to show no sign of geomagnetic jerks, which are seen in  o above the Earth’s surface at various epochs (Fig. 3); particularly, the eastward component of
o above the Earth’s surface at various epochs (Fig. 3); particularly, the eastward component of  na is not at all correlated with the well-specified geomagnetic jerks at the Niemegk (NGK) and Hermanus (HER) observatories around the epochs 1970, 1980 and 1991. This suggests that the observed geomagnetic jerks are almost consistent with the FF assumption and that they do not have to be attributed to either the advection of unknown smaller-scale MF or the diffusion. Considering that
na is not at all correlated with the well-specified geomagnetic jerks at the Niemegk (NGK) and Hermanus (HER) observatories around the epochs 1970, 1980 and 1991. This suggests that the observed geomagnetic jerks are almost consistent with the FF assumption and that they do not have to be attributed to either the advection of unknown smaller-scale MF or the diffusion. Considering that  na at the CMB consists of field changes that are very localized (Fig. 2), it may be natural that its upward continuation fails to explain the global-scale geomagnetic jerks above the Earth’s surface. Indeed, little correlation is acknowledged between the individual SV coefficients from
na at the CMB consists of field changes that are very localized (Fig. 2), it may be natural that its upward continuation fails to explain the global-scale geomagnetic jerks above the Earth’s surface. Indeed, little correlation is acknowledged between the individual SV coefficients from  o and
o and  na at lower degrees (Fig. 4). The 1969 geomagnetic jerk appears relatively explicitly in the time series of
na at lower degrees (Fig. 4). The 1969 geomagnetic jerk appears relatively explicitly in the time series of  -component of
-component of  o, but not at all in that component of
o, but not at all in that component of  na. The secular decay of the axial dipole intensity, represented by the positive offset of
na. The secular decay of the axial dipole intensity, represented by the positive offset of  -component of
-component of  o, is partly assigned to the non-advective SV, but not persistently for the whole period covered by CM4 model.
o, is partly assigned to the non-advective SV, but not persistently for the whole period covered by CM4 model.
(a) The vertical downward component of the input SV (black curve) and non-advective SV (gray curve) from GRIMM (2002.0–2005.0) at 34°N, 77°E and 17°S, 107°E, both at 400 km altitude. (b) The eastward component of the input SV (black curve) and non-advective SV (gray curve) from CM4 (1960.0–2002.0) at NGK (52°N, 13°E, 0 km) and HER (34°S, 19°E, 0 km).
5.2 Non-geostrophic SV
The singular values λj of Atg for GRIMM at 2003.5 and CM4 at 1980.0 are shown in Fig. 5. We confirm that all of them are non-zero up to number  , for both GRIMM and CM4 models and all epochs. The estimated errors of λj assure that they are unaffected by the variances of i bo defined as in the previous subsection. Hence, calculation of the non-geostrophic SV coefficients
, for both GRIMM and CM4 models and all epochs. The estimated errors of λj assure that they are unaffected by the variances of i bo defined as in the previous subsection. Hence, calculation of the non-geostrophic SV coefficients  ng is done using Eq. (11) with
ng is done using Eq. (11) with  .
.
The snapshots of radial components of input SV ( o)r and non-geostrophic SV (
o)r and non-geostrophic SV ( ng)r at the CMB are displayed in Fig. 6. They indicate that (
ng)r at the CMB are displayed in Fig. 6. They indicate that ( ng)r has a power noticeably greater than (
ng)r has a power noticeably greater than ( na)r. It is especially notable that (
na)r. It is especially notable that ( ng)r and (
ng)r and ( o)r have a similar magnitude below Eurasia and Central America, where (
o)r have a similar magnitude below Eurasia and Central America, where ( na)r has little power (Fig. 2). This is basically due to the number of the bases uj for
na)r has little power (Fig. 2). This is basically due to the number of the bases uj for  ng, which is by far larger than that for
ng, which is by far larger than that for  na. Indeed, the FF+TG condition used here reduces the degree of freedom of
na. Indeed, the FF+TG condition used here reduces the degree of freedom of  ge (and accordingly increases the dimension of
ge (and accordingly increases the dimension of  ng)byasmanyas NSV - p = 792 (for the case with GRIMM). Note that the CH’s FF+TG condition is even stronger, consisting of an infinite number of integrals defined throughout the CMB (Chulliat and Hulot, 2001).
ng)byasmanyas NSV - p = 792 (for the case with GRIMM). Note that the CH’s FF+TG condition is even stronger, consisting of an infinite number of integrals defined throughout the CMB (Chulliat and Hulot, 2001).
At some areas above the Earth’s surface, the temporal evolution of  ng has a correlation with
ng has a correlation with  o, which is significantly higher than that shown by the evolution of
o, which is significantly higher than that shown by the evolution of  na. At NGK, the eastward component of
na. At NGK, the eastward component of  ng shows fluctuations in phase with the geomagnetic jerks of
ng shows fluctuations in phase with the geomagnetic jerks of  o (Fig. 7), whereas no such fluctuations are seen for that of
o (Fig. 7), whereas no such fluctuations are seen for that of  na (Fig. 3). Similarly, at HER, the fluctuations of the eastward component of
na (Fig. 3). Similarly, at HER, the fluctuations of the eastward component of  o is correlated more highly with that of
o is correlated more highly with that of  ng than that of
ng than that of  na, though no geomagnetic jerk is recognizable for either one around 1970. Thus, the geomagnetic jerks of the input SV models partly require a contribution of non-geostrophic SV. The globalness of this non-geostrophic SV contribution can be confirmed in the individual coefficients of
na, though no geomagnetic jerk is recognizable for either one around 1970. Thus, the geomagnetic jerks of the input SV models partly require a contribution of non-geostrophic SV. The globalness of this non-geostrophic SV contribution can be confirmed in the individual coefficients of  ng at low degrees; some components of
ng at low degrees; some components of  ng and
ng and  o at degrees 1 and 2 are apparently in phase (Fig. 8).
o at degrees 1 and 2 are apparently in phase (Fig. 8).
(a) The vertical downward component of the input SV (black curve) and non-geostrophic SV (gray curve) from GRIMM (2002.0–2005.0) at 34°N, 77°E and 17°S, 107°E, both at 400 km altitude. (b) The eastward component of the input SV (black curve) and non-geostrophic SV (gray curve) from CM4 (1960.0–2002.0) at NGK (52°N, 13°E, 0 km) and HER (34°S, 19°E, 0 km).
The  -component of
-component of  ng shows a remarkable fit to that of
ng shows a remarkable fit to that of  o. This indicates that the secular decay of the axial dipole intensity is mostly inconsistent with the FF+TG condition at the CMB, forming the part of observed SV that is unpredictable by the TG flow. Indeed, TG flow inversions tend to result in models that underfit the
o. This indicates that the secular decay of the axial dipole intensity is mostly inconsistent with the FF+TG condition at the CMB, forming the part of observed SV that is unpredictable by the TG flow. Indeed, TG flow inversions tend to result in models that underfit the  coefficient (Jackson, 1997). Note that these TG flow models can still explain the axial dipole decay to within its error, though our analysis indicates the significant incompatibility of the decay and the FF+TG condition. This comes from the fact that the inversions simply minimize SV misfit only up to the truncation degree of a given SV model, while we consider the FF+TG condition, including all possible SV prediction at the CMB.
coefficient (Jackson, 1997). Note that these TG flow models can still explain the axial dipole decay to within its error, though our analysis indicates the significant incompatibility of the decay and the FF+TG condition. This comes from the fact that the inversions simply minimize SV misfit only up to the truncation degree of a given SV model, while we consider the FF+TG condition, including all possible SV prediction at the CMB.
5.3 Robustness of results
Here, we address questions regarding the robustness of our results before interpreting them in the next section. While no ambiguity has been discovered in selecting p at any epoch and, consequently, in the number of the SV coefficient bases uj forming  na or
na or  ng, several factors still remain in our approach that can subsequently alter our results, including the definition of the scalar product in the spatial domain and the truncation degree LMF of input MF and SV models. Indeed, the results in the previous subsections can be flawed by artifacts, if the assumptions for the choices of the scalar product or the truncation degree are inappropriate for the true core. It is therefore worth investigating alternative choices to identify robust or unrealistic features of the various results.
ng, several factors still remain in our approach that can subsequently alter our results, including the definition of the scalar product in the spatial domain and the truncation degree LMF of input MF and SV models. Indeed, the results in the previous subsections can be flawed by artifacts, if the assumptions for the choices of the scalar product or the truncation degree are inappropriate for the true core. It is therefore worth investigating alternative choices to identify robust or unrealistic features of the various results.
The SV coefficients  have been defined such that the two squared norms,
have been defined such that the two squared norms,  T
T  and
and  , are both equal to the energy of
, are both equal to the energy of  r integrated over the core surface r = c, according to our choice of the scalar product (7). Mathematically, it is possible to take any other kind of scalar quantity for
r integrated over the core surface r = c, according to our choice of the scalar product (7). Mathematically, it is possible to take any other kind of scalar quantity for  . For example, one may take
. For example, one may take  as an alternative definition for Eq. (7), in which case
as an alternative definition for Eq. (7), in which case  represents the total field energy of
represents the total field energy of  integrated over r = c. We have checked, nevertheless, that the results are not significantly changed; the non-advective or non-geostrophic SV are still very similar to those shown in the previous subsections. This is simply because the new weight matrix
integrated over r = c. We have checked, nevertheless, that the results are not significantly changed; the non-advective or non-geostrophic SV are still very similar to those shown in the previous subsections. This is simply because the new weight matrix  , to be used instead of Eq. (10), has elements that differ only by a factor of 1.5 to 2.0 from those given by Eq. (10). We have also made a test with the heat norm using
, to be used instead of Eq. (10), has elements that differ only by a factor of 1.5 to 2.0 from those given by Eq. (10). We have also made a test with the heat norm using  (Gubbins, 1975; Bloxham and Jackson, 1992). The subsequent non-advective SV still shows no siginificant differences, though it has slightly higher (resp. lower) powers at low (resp. high) SH degrees.
(Gubbins, 1975; Bloxham and Jackson, 1992). The subsequent non-advective SV still shows no siginificant differences, though it has slightly higher (resp. lower) powers at low (resp. high) SH degrees.
The weight matrix W1/2 is much more sensitive to the radius r of spherical surface for which the scalar product  is defined, as it is proportional to r raised to the power of (l + 2). We have actually found that the results are seriously affected by the radius r defining the scalar product. If it is defined as
is defined, as it is proportional to r raised to the power of (l + 2). We have actually found that the results are seriously affected by the radius r defining the scalar product. If it is defined as

with the radius r = a' of 400 km altitude (i.e. around satellite altitude), the resulting non-advective SV  (and non-geostrophic SV
(and non-geostrophic SV  ) has a very small magnitude compared with
) has a very small magnitude compared with  o at r = a'. To show the variability of the results, we plot in Fig. 9 the time-averaged power spectra (with respect to r = c and a') of the two non-advective SVs
o at r = a'. To show the variability of the results, we plot in Fig. 9 the time-averaged power spectra (with respect to r = c and a') of the two non-advective SVs  na and
na and  , computed with the scalar products (7) and (12), respectively. Their spectra are very different, whereas both of their total unsigned flux changes
, computed with the scalar products (7) and (12), respectively. Their spectra are very different, whereas both of their total unsigned flux changes  (Eq. (3)) are still equal to that of
(Eq. (3)) are still equal to that of  o. The spectrum of
o. The spectrum of  is unrealistic, with its power concentrated only at the very high degrees. We therefore prefer the definition (7) to (12), considering the spectra of resulting non-advective SVs.
is unrealistic, with its power concentrated only at the very high degrees. We therefore prefer the definition (7) to (12), considering the spectra of resulting non-advective SVs.
Time-averaged spectra of the input SV  o from GRIMM (2002.0–2005.0) (black curve), and the non-advective SVs
o from GRIMM (2002.0–2005.0) (black curve), and the non-advective SVs  na (light gray curve) and
na (light gray curve) and  (dark gray curve) computed with the definitions of scalar products (7) and (12), respectively. Each spectrum is plotted with respect to the mean core radius (solid) and 400 km altitude (dashed).
(dark gray curve) computed with the definitions of scalar products (7) and (12), respectively. Each spectrum is plotted with respect to the mean core radius (solid) and 400 km altitude (dashed).
Changing the truncation degree LMF of input models has an impact on the mapping of the geomagnetic field at the CMB, because the higher degree components are more amplified when downward continued. Indeed, it has been estimated that at the CMB the SV power increases with degrees (Voorhies, 2004; Holme and Olsen, 2006). The results of the present analysis should vary considerably with LMF. To reveal the dependence of our analysis on the selection of LMF, we perform the same analyses of CM4 with different LMF. First,  na and
na and  ng are computed from CM4 truncated at degree LMF = 8 (they are here denoted by
ng are computed from CM4 truncated at degree LMF = 8 (they are here denoted by  and
and  , respectively). We then find similar features between the time evolutions of
, respectively). We then find similar features between the time evolutions of  and
and  . For example,
. For example,  fails to reproduce the geomagnetic jerk signals at NGK, as is the case with
fails to reproduce the geomagnetic jerk signals at NGK, as is the case with  (Fig. 10(a)). Further, time evolutions of the low degree components of
(Fig. 10(a)). Further, time evolutions of the low degree components of  are similar to those of the corresponding components of
are similar to those of the corresponding components of  . All of them are uncorrelated with those of
. All of them are uncorrelated with those of  o; for example, the
o; for example, the  and
and  components of
components of  are shown in Fig. 11(a). The time evolutions of
are shown in Fig. 11(a). The time evolutions of  and
and  are also similar, in that they basically show most of the geomagnetic jerk signals. For example,
are also similar, in that they basically show most of the geomagnetic jerk signals. For example,  has geomagnetic jerk signals at NGK except in 1991 (Fig. 10(b)). Moreover, the
has geomagnetic jerk signals at NGK except in 1991 (Fig. 10(b)). Moreover, the  components of
components of  o and
o and  agree well (Fig. 11(b)).
agree well (Fig. 11(b)).
The eastward component of the input SV (black solid curve) and (a) the non-advective SVs and (b) the non-geostrophic SVs from CM4 (1960.0–2002.0) at NGK. The non-advective and non-geostrophic SVs are computed with the truncation degrees LMF = 8 (light gray curve), 13 (dark gray curve), and 18 (dashed, dotted and dot-dashed curves). For LMF = 18, three results are plotted in accordance with different sets of the synthetic coefficients  and
and  (14 = l = 18) generated using Eqs. (13) and (14), with phase parameters
(14 = l = 18) generated using Eqs. (13) and (14), with phase parameters  selected three times randomly.
selected three times randomly.
The  and
and  components of the Gauss coefficients (not renormalized) for the input SV
components of the Gauss coefficients (not renormalized) for the input SV  o (black solid curve) compared with the same components for (a) the non-advective SV
o (black solid curve) compared with the same components for (a) the non-advective SV  na and (b) the non-geostrophic SV
na and (b) the non-geostrophic SV  ng computed from CM4 for 1960.0–2002.0, with the truncation degrees LMF = 8 (light gray curve), 13 (dark gray curve), and 18 (dashed, dotted and dot-dashed curves). For LMF = 18, three results are plotted in accordance with different sets of the synthetic coefficients
ng computed from CM4 for 1960.0–2002.0, with the truncation degrees LMF = 8 (light gray curve), 13 (dark gray curve), and 18 (dashed, dotted and dot-dashed curves). For LMF = 18, three results are plotted in accordance with different sets of the synthetic coefficients  and
and  (14 = l = 18) generated using Eqs. (13) and (14), with phase parameters selected three times randomly.
(14 = l = 18) generated using Eqs. (13) and (14), with phase parameters selected three times randomly.
The same analysis is done with LMF larger than 13. Since CM4 has zero core field coefficients above degree 13, we supplement the model with synthetic coefficients at those degrees. They are synthesized as


where  represents the conventional Gauss coefficient
represents the conventional Gauss coefficient  or
or  for the core field with l > 13 (not renormalized with W1/2), and t is the time in year.
for the core field with l > 13 (not renormalized with W1/2), and t is the time in year.  is the power spectrum of MF at
is the power spectrum of MF at  is the power ratio of SV to MF as a function of degree l, and
is the power ratio of SV to MF as a function of degree l, and  is an arbitrary phase parameter. This formulation of synthetic coefficients is such that they vary around zero mean with a time constant of (S(l))-1/2 year. The definitions of R(l) and S(l) are consistent with the synthetic coefficients averaged in time; their time-averaged squares,
is an arbitrary phase parameter. This formulation of synthetic coefficients is such that they vary around zero mean with a time constant of (S(l))-1/2 year. The definitions of R(l) and S(l) are consistent with the synthetic coefficients averaged in time; their time-averaged squares,  , give statistical expected variances of
, give statistical expected variances of  in accordance with the power spectrum R(l) (they are assumed to be uncorrelated to one another). For the computation of the synthetic coefficients, we use
in accordance with the power spectrum R(l) (they are assumed to be uncorrelated to one another). For the computation of the synthetic coefficients, we use

with  after Pais and Jault (2008),
after Pais and Jault (2008),

as suggested by Lesur et al. (2008), and  randomly set for each coefficient.
randomly set for each coefficient.
Figures 10(a) and 11(a) show three results of non-advective SV  obtained using three different sets of MF
obtained using three different sets of MF  and SV
and SV  consisting of CM4 and synthetic coefficients up to degree LMF= 18. Their time variations are not really correlated with the geomagnetic jerks, but have amplitudes larger than those of
consisting of CM4 and synthetic coefficients up to degree LMF= 18. Their time variations are not really correlated with the geomagnetic jerks, but have amplitudes larger than those of  and
and  . It is implied that advection on the unresolved scales may contribute to the non-advective SV. Furthermore, the increased amplitude of
. It is implied that advection on the unresolved scales may contribute to the non-advective SV. Furthermore, the increased amplitude of  is not just due to the energy of
is not just due to the energy of  increased by adding the synthetic SV. We linearly decompose
increased by adding the synthetic SV. We linearly decompose  into its parts, each resulting from the original CM4 SV
into its parts, each resulting from the original CM4 SV  (up to SH degree 13) and the synthetic SV
(up to SH degree 13) and the synthetic SV  , to find that the increased amplitude is associated with both parts of
, to find that the increased amplitude is associated with both parts of  . This means that even when the SV model only up to degree 13 is used as an input SV, the amplitude of non-advective SV is increased by the complexity of the radial field map of
. This means that even when the SV model only up to degree 13 is used as an input SV, the amplitude of non-advective SV is increased by the complexity of the radial field map of  at the CMB due to an inclusion of synthetic MF. This seems in contrast with the findings of Gillet et al. (2009), who investigate the source of FF violation using CM4 MF and SV up to degree 13 and synthetic MF at higher degrees. They discuss that the small-scale MF is not the main cause of the FF violation. Their argument is derived from the analysis based on the flow models which are built using a damping of the higher degree components. Our incompatible statement might come from the absence of limitation with regard to the flow. We examine only field models; even flows with physically unacceptable behaviors are considered in our analysis. In addition, our FF condition is stronger in reducing the degree of freedom of
at the CMB due to an inclusion of synthetic MF. This seems in contrast with the findings of Gillet et al. (2009), who investigate the source of FF violation using CM4 MF and SV up to degree 13 and synthetic MF at higher degrees. They discuss that the small-scale MF is not the main cause of the FF violation. Their argument is derived from the analysis based on the flow models which are built using a damping of the higher degree components. Our incompatible statement might come from the absence of limitation with regard to the flow. We examine only field models; even flows with physically unacceptable behaviors are considered in our analysis. In addition, our FF condition is stronger in reducing the degree of freedom of  ad than the ones they study, i.e. the temporal change of flux in a single patch and the temporal change of the total unsigned flux.
ad than the ones they study, i.e. the temporal change of flux in a single patch and the temporal change of the total unsigned flux.
We also compute non-advective SVs  obtained with LMF = 26, and again confirm that their time variations, which are all out of phase with the geomagnetic jerks, have amplitudes similar to those of
obtained with LMF = 26, and again confirm that their time variations, which are all out of phase with the geomagnetic jerks, have amplitudes similar to those of  as presented in Figs. 10(a) and 11(a). Gillet et al. (2009) introduce an exponential law fit to S(l) (as opposed to the power law fit by Lesur et al. (2008)) for extraporating the time constant to the unresolved scales. In such a case, both S(l) and the SV power spectrum at the CMB increase even more rapidly with l above degree 13, with the SV power at these degrees becoming significantly larger than the power of the synthesized SV in this study. Subsequent
as presented in Figs. 10(a) and 11(a). Gillet et al. (2009) introduce an exponential law fit to S(l) (as opposed to the power law fit by Lesur et al. (2008)) for extraporating the time constant to the unresolved scales. In such a case, both S(l) and the SV power spectrum at the CMB increase even more rapidly with l above degree 13, with the SV power at these degrees becoming significantly larger than the power of the synthesized SV in this study. Subsequent  na may even have a larger amplitude varying with shorter timescales. It seems unlikely, nevertheless, that
na may even have a larger amplitude varying with shorter timescales. It seems unlikely, nevertheless, that  na happens to gain a correlation with the successive geomagnetic jerks. We can at least regard it as robust that
na happens to gain a correlation with the successive geomagnetic jerks. We can at least regard it as robust that  na does not have to be correlated with the geomagnetic jerks.
na does not have to be correlated with the geomagnetic jerks.
On the other hand, non-geostrophic SVs  obtained with LMF = 18 evolve in phase with
obtained with LMF = 18 evolve in phase with  o (Figs. 10(b) and 11(b)). They clearly exhibit the features of the geomagnetic jerks. Furthermore, there is again a persistent agreement of the
o (Figs. 10(b) and 11(b)). They clearly exhibit the features of the geomagnetic jerks. Furthermore, there is again a persistent agreement of the  components of
components of  and
and  (Fig. 11(b)). These findings are also seen in
(Fig. 11(b)). These findings are also seen in  obtained with LMF = 26. This indicates that the typical behavior of
obtained with LMF = 26. This indicates that the typical behavior of  ng at the lowest SH degrees is not so sensitive to the unresolved small-scale interactions between the MF and flow, as far as the R(l) and S(l) used here are considered, and MF and SV models have the same truncation degree (at least up to 26). We conclude that the characteristics of
ng at the lowest SH degrees is not so sensitive to the unresolved small-scale interactions between the MF and flow, as far as the R(l) and S(l) used here are considered, and MF and SV models have the same truncation degree (at least up to 26). We conclude that the characteristics of  ng shown in the previous subsection appear to be robust, in a qualitative sense.
ng shown in the previous subsection appear to be robust, in a qualitative sense.
6. Discussion
The non-advective and non-geostrophic SVs extracted from the GRIMM and CM4 models can be indicative of some different core processes. As the potential contribution of unresolved scale advection to the large-scale SV is not negligible (Pais and Jault, 2008), this contribution to the computed non-advective and non-geostrophic SVs cannot be ruled out. Nevertheless, we are here most interested in discussing the possible diffusion contribution to our computation results. The following discussions rely on  na and
na and  ng computed with LMF = 13, whose time variations and spatial distributions are presented in Subsections 5.1 and 5.2.
ng computed with LMF = 13, whose time variations and spatial distributions are presented in Subsections 5.1 and 5.2.
The computed  na suggests that the non-advective SV is localized and makes up only a minor fraction of the whole SV. The local intensive spots of (
na suggests that the non-advective SV is localized and makes up only a minor fraction of the whole SV. The local intensive spots of ( na)r at the CMB, evolving gradually as the null-flux curves nearby change their configuration, may indicate the area of diffusion associated with the flux expulsion (Bloxham, 1986; Gubbins, 2007). The rapid fluctuations of the large-scale components (excluding the axial dipole component) of
na)r at the CMB, evolving gradually as the null-flux curves nearby change their configuration, may indicate the area of diffusion associated with the flux expulsion (Bloxham, 1986; Gubbins, 2007). The rapid fluctuations of the large-scale components (excluding the axial dipole component) of  o, such as the global geomagnetic jerks, are not attributed to those of
o, such as the global geomagnetic jerks, are not attributed to those of  na, which vary rather slowly in time (Fig. 4). This is more or less consistent with the arguments of steady diffusion (Voorhies, 1993; Love, 1999) as well as with the arguments for the primary contribution of the advection to the geomagnetic jerks (Bloxham et al., 2002; Olsen and Mandea, 2008; Wardinski et al., 2008).
na, which vary rather slowly in time (Fig. 4). This is more or less consistent with the arguments of steady diffusion (Voorhies, 1993; Love, 1999) as well as with the arguments for the primary contribution of the advection to the geomagnetic jerks (Bloxham et al., 2002; Olsen and Mandea, 2008; Wardinski et al., 2008).
The axial dipole component of  na behaves in a different way than other components of
na behaves in a different way than other components of  na at low SH degrees, exhibiting relatively rapid variations associated with the amplitude of ~20 nT/yr. This is in contrast with the same component of
na at low SH degrees, exhibiting relatively rapid variations associated with the amplitude of ~20 nT/yr. This is in contrast with the same component of  o representing the secular decay of the axial dipole intensity. The decay is at least of centennial timescales (Finlay, 2008), which apparently applies to the arguments of steady diffusion. However, considering the FF condition alone does not necessarily require that the secular decay be totally due to diffusion (at least for the period of CM4). The decay may be due to both the diffusive process, i.e. the growth of reverse patches in the Southern Hemisphere, and the advective process, i.e. the poleward migration of the reverse patches (Gubbins et al., 2006).
o representing the secular decay of the axial dipole intensity. The decay is at least of centennial timescales (Finlay, 2008), which apparently applies to the arguments of steady diffusion. However, considering the FF condition alone does not necessarily require that the secular decay be totally due to diffusion (at least for the period of CM4). The decay may be due to both the diffusive process, i.e. the growth of reverse patches in the Southern Hemisphere, and the advective process, i.e. the poleward migration of the reverse patches (Gubbins et al., 2006).
The computed  ng suggests that the input models
ng suggests that the input models  o are poorly consistent with the FF+TG condition (as shown in Fig. 6), indicating that (
o are poorly consistent with the FF+TG condition (as shown in Fig. 6), indicating that ( o)r substantially involves (
o)r substantially involves ( ng)r throughout the CMB. The non-geostrophic SV can be due to the advection by the ageostrophic flow in the equatorial regions where TG assumption tends to fail. Most regions at mid- and high latitudes are covered by the ‘geostrophic region’ (Chulliat and Hulot, 2001), so (
ng)r throughout the CMB. The non-geostrophic SV can be due to the advection by the ageostrophic flow in the equatorial regions where TG assumption tends to fail. Most regions at mid- and high latitudes are covered by the ‘geostrophic region’ (Chulliat and Hulot, 2001), so ( ng)r should not arise from the ageostrophic flow. It then follows that, in such regions,
ng)r should not arise from the ageostrophic flow. It then follows that, in such regions,  ng more probably originates in the diffusion processes. It seems physically difficult, nevertheless, to attribute the computed
ng more probably originates in the diffusion processes. It seems physically difficult, nevertheless, to attribute the computed  ng entirely to diffusion. According to the time-series map of (
ng entirely to diffusion. According to the time-series map of ( ng)r over the CMB, its local intensive patterns do not hold for a long duration. They vary on timescales no longer than a decade, possibly in correspondence to the geomagnetic jerk occurences. If these rapid processes are due to diffusion, the field fluctuations should be generated in a thin region close to the core surface, with a thickness equivalent to the skin depth of the order ~104 m. Braginsky and Le Mouël (1993) and Jault and Le Mouël (1994) have examined the effect of such a thin layer in which the flow is driven by a dynamics distinct from that within the underlying volume of the core and claimed that a significant diffusion occurs in response to fluctuations of horizontal flow therein. They have also argued that the resulting SV can still be consistent with the FF condition, if the flow at the very surface of the core is replaced by an averaged flow in the layer. This type of diffusion could thus contribute to
ng)r over the CMB, its local intensive patterns do not hold for a long duration. They vary on timescales no longer than a decade, possibly in correspondence to the geomagnetic jerk occurences. If these rapid processes are due to diffusion, the field fluctuations should be generated in a thin region close to the core surface, with a thickness equivalent to the skin depth of the order ~104 m. Braginsky and Le Mouël (1993) and Jault and Le Mouël (1994) have examined the effect of such a thin layer in which the flow is driven by a dynamics distinct from that within the underlying volume of the core and claimed that a significant diffusion occurs in response to fluctuations of horizontal flow therein. They have also argued that the resulting SV can still be consistent with the FF condition, if the flow at the very surface of the core is replaced by an averaged flow in the layer. This type of diffusion could thus contribute to  ge. It is unlikely that the rapidly fluctuating
ge. It is unlikely that the rapidly fluctuating  ng is explained by the diffusion of the flux expulsion type, unless a turbulence with significant kinetic and magnetic energies is assumed in the thin layer.
ng is explained by the diffusion of the flux expulsion type, unless a turbulence with significant kinetic and magnetic energies is assumed in the thin layer.
Unlike other components of  ng, its axial dipole component does not fluctuate significantly in time. In fact, it agrees very well with the secular decay of the axial dipole (Fig. 8). If the decay arises from the poleward advection of reverse patches (Gubbins et al., 2006), then it has to be caused by the ageostrophic flow. It is not plausible, however, that the ageostrophic flow prevails at higher latitudes. We therefore would attribute the secular decay to the growth of reverse patches, rather than to the poleward migration of the patches.
ng, its axial dipole component does not fluctuate significantly in time. In fact, it agrees very well with the secular decay of the axial dipole (Fig. 8). If the decay arises from the poleward advection of reverse patches (Gubbins et al., 2006), then it has to be caused by the ageostrophic flow. It is not plausible, however, that the ageostrophic flow prevails at higher latitudes. We therefore would attribute the secular decay to the growth of reverse patches, rather than to the poleward migration of the patches.
Our study has focused on investigating the given geomagnetic models, but there is still a possibility of modifying them so that the FF and TG assumptions may hold thoughout the CMB. Once a SV model is allowed to have a certain amount of power due to the non-zero coefficients above degree LMF, there is little difficulty to render the SV model subject to the FF+TG condition. This has already been indicated by  and
and  obtained with the scalar product (12). Because of their insignificance at all degrees at the Earth’s surface or at 400 km altitude (r = a') (see Fig. 9 for the case with
obtained with the scalar product (12). Because of their insignificance at all degrees at the Earth’s surface or at 400 km altitude (r = a') (see Fig. 9 for the case with  at r = a'), the residual parts
at r = a'), the residual parts  and
and  fit to
fit to  o very well there, each still satisfying the FF and FF+TG conditions at the CMB. As a matter of fact, the Gauss coefficients of
o very well there, each still satisfying the FF and FF+TG conditions at the CMB. As a matter of fact, the Gauss coefficients of  and
and  are almost identical to those of
are almost identical to those of  o. The time-averaged rms magnitude of
o. The time-averaged rms magnitude of  , i.e. rms misfit between
, i.e. rms misfit between  and
and  o, from GRIMM at r = a' is only as much as 6.0 × 10-4 nT yr-1. This is by far smaller than the accuracy of GRIMM. Of course,
o, from GRIMM at r = a' is only as much as 6.0 × 10-4 nT yr-1. This is by far smaller than the accuracy of GRIMM. Of course,  is an extreme example of the geostrophic SV, having the unrealistic spectrum with very high powers concentrated at degrees above LMF. Nevertheless, one may be able to create a magnetic model consisting exclusively of the geostrophic SV, by allowing for the ‘unknown SV’ above its truncation degree of the given models, which is associated with significant power at r = c, but observationally insignificant above the Earth’s surface.
is an extreme example of the geostrophic SV, having the unrealistic spectrum with very high powers concentrated at degrees above LMF. Nevertheless, one may be able to create a magnetic model consisting exclusively of the geostrophic SV, by allowing for the ‘unknown SV’ above its truncation degree of the given models, which is associated with significant power at r = c, but observationally insignificant above the Earth’s surface.
7. Conclusions
With the SH domain approach, a snapshot of the part of SV violating the necessary condition of FF or FF+TG assumption can be built over the CMB. We have avoided the non-uniqueness in decomposing the SV into two parts violating and satisfying the necessary condition, by assuming the orthogonality of the two parts in terms of radial SV energy integrated over the CMB. This approach is advantageous in that geometric and topologic constraints, such as number and morphology of the null-flux curves, do not have to be considered for the necessary conditions.
We have revealed that the GRIMM and CM4 core field models, when each is truncated at the same degree for both MF and SV models, evidently involve the non-advective SV violating the FF condition and also the non-geostrophic SV violating the FF+TG condition. The radial component of the non-advective SV emerges mainly within small null-flux patches at the CMB. A local intensive area is also found in the neighborhood of the undulating null-flux curve at the magnetic equator. The time variation of the non-advective SV is not correlated with the geomagnetic jerks, indicating that these short-time events (as described by GRIMM and CM4) do not have to involve the diffusion process. In contrast with the non-advective SV, the radial component of non-geostrophic SV prevails throughout the core surface, for the two investigated models. Of particular interest is that the non-geostrophic SV shows short-term variations correlated with the geomagentic jerks. Further, the most part of the secular decay of the axial dipole field is due to the non-geostrophic SV. These findings are unlikely to depend on the truncation degree of the input field models, as long as both MF and SV models have the same truncation degree (at least up to 18) and moderate trends in their power spectra.
As the core flow is plausibly in the TG balance over a large area of the core surface, a majority of the non-geostrophic SV should not originate from the advection of radial MF by the ageostrophic flow. The diffusion is therefore a possible source of the steadily positive axial dipole component of the non-geostrophic SV, as well as its slowly evolving components which are also seen in the non-advective SV. Yet, the diffusion is practically unlikely to explain the non-geostrophic SV which fluctuates rapidly, producing a part of the observed geomagnetic jerks. This is possibly explained by the presence of fluctuating ageostrophic flow near the geographic equator, just as required for explaining the latest secular variation fluctuations (Olsen and Mandea, 2008). We note, nevertheless, that one cannot discard the possibility of appropriately modifying the SV models to meet the FF+TG condition completely. This can be achieved by allowing the unknown SV at degrees above the truncation degree of the given models to have a dominant power at the CMB.
The method of the present analysis is restricted to a given single epoch. We have examined an instantaneous SV model sequentially for each different epoch against the instantaneous necessary condition for a prescribed MF. We have not studied the MF models. Further, we have not extended our study to examine the entire span of field models at once. The method would then require a huge computation, while it is theoretically feasible if the scalar product we have defined for a certain epoch is somehow extended to involve the total time span. A practical and more comprehensive test of the observed field against the conditions would be to assess simultaneously the existence of reasonable MF, SV and flow models that are temporally continuous and compatible with the FF or FF+TG condition (Lesur et al., 2010). In constructing such a comprehensive field model, the SH domain approach would be an effective alternative to the modelling approaches directly allowing for the surface integral conditions in the spatial domain (Gubbins, 1984; Bloxham and Gubbins, 1986; Constable et al., 1993; O’Brien et al., 1997; Jackson et al., 2007).
References
Backus, G. E., Kinematics of geomagnetic secular variation in a perfectly conducting core, Phil. Trans. R. Soc. Lond. A, 263, 239–266, 1968.
Backus, G. E. and J.-L. Le Mouël, The region of the core-mantle boundary where a geostrophic velocity field can be determined from frozen-flux magnetic data, Geophys. J. R. Astron. Soc., 85, 618–627, 1986.
Benton, E. R. and M. A. Celaya, The simplest, unsteady surface flow of a frozen-flux core that exactly fits a geomagnetic field model, Geophys. Res. Lett., 18, 577–580, 1991.
Bloxham, J., The expulsion of magnetic flux from the Earth’s core, Geophys. J. R. Astron. Soc., 87, 669–678, 1986.
Bloxham, J., The determination of fluid flow at the core surface from geomagnetic observation, in Mathematical Geophysics, A Survey of Recent Developments in Seismology and Geodynamics, edited by V. J. Vlaar et al., pp. 189–208, D. Reodel Publishing Company, Hingham, Massachusetts, 1988.
Bloxham, J. and D. Gubbins, The secular variation of Earth’s magnetic field, Nature, 317, 777–781, 1985.
Bloxham, J. and D. Gubbins, Geomagnetic field analysis—IV. Testing the frozen-flux hypothesis, Geophys. J. R. Astron. Soc., 84, 139–152, 1986.
Bloxham, J. and A. Jackson, Fluid flow near the surface of Earth’s outer core, Rev. Geophys., 29, 97–120, 1991.
Bloxham, J. and A. Jackson, Time-dependent mapping of the magnetic field at the core-mantle boundary, J. Geophys. Res., 97, 19537–19563, 1992.
Bloxham, J., S. Zatman, and M. Dumberry, The origin of geomagnetic jerks, Nature, 420, 65–68, 2002.
Bondi, H. and T. Gold, On the generation of magnetism by fluid motion, Mon. Not. R. Astron. Soc., 110, 607–611, 1950.
Braginsky, S. I. and J. L. Le Mouël, Two-scale model of a geomagnetic field variation, Geophys. J. Int., 112, 147–158, 1993.
Chambodut, A. and M. Mandea, Evidence for geomagnetic jerks in comprehensive models, Earth Planets Space, 57, 139–149, 2005.
Chulliat, A. and G. Hulot, Geomagnetic secular variation generated by a tangentially geostrophic flow under the frozen-flux assumption—I. Necessary conditions, Geophys. J. Int., 147, 237–246, 2001.
Constable, C. G., R. L. Parker, and P. B. Stark, Geomagnetic field models incorprating frozen-flux constraints, Geophys. J. Int., 113, 419–433, 1993.
Eymin, C. and G. Hulot, On core surface flows inferred from satellite magnetic data, Phys. Earth Planet. Inter., 152, 200–220, 2005.
Finlay, C. C., Historical variations of the geomagnetic axial dipole, Phys. Earth Planet. Inter., 170, 1–14, 2008.
Gillet, N., M. A. Pais, and D. Jault, Ensemble inversion of time-dependent core flow models, Geochem. Geophys. Geosyst., 10, 2008GC002290, 2009.
Gire, C. and J.-L. Le Mouël, Tangentially geostrophic flow at the core-mantle boundary compatible with the observed geomagnetic seculat variation: the large-scale component of the flow, Phys. Earth Planet. Inter., 59, 259–287, 1990.
Gubbins, D., Can the Earth’s magnetic field be sustained by core oscillation?, Geophys. Res. Lett., 2, 409–412, 1975.
Gubbins, D., Geomagnetic field analysis—II. Secular variation consistent with a perfectly conducting core, Geophys. J. R. Astron. Soc., 77, 753–766, 1984.
Gubbins, D., Dynamics of the secular variation, Phys. Earth Planet. Inter., 68, 170–182, 1991.
Gubbins, D., A formalism for the inversion of geomagnetic data for core motions with diffusion, Phys. Earth Planet. Inter., 98, 193–206, 1996.
Gubbins, D., Geomagnetic constraint on stratification at the top of the core, Earth Planets Space, 59, 661–664, 2007.
Gubbins, D. and P. Roberts, Magnetohydrodynamics of the Earth’s core, in Geomagnetism, edited by Jacobs, J. A., vol. 2, pp. 249–512, Academic Press, New York, 1987.
Gubbins, D., A. L. Jones, and C. Finlay, Fall in Earth’s magnetic field is erratic, Science, 312, 900–903, 2006.
Holme, R., Large scale flow in the core, in Treatise in Geophysics, Core Dynamics, edited by Olson, P. and G. Schubert, vol. 8, pp. 107–129, 2007.
Holme, R. and N. Olsen, Core surface flow modelling from high-resolution secular variaion, Geophys. J. Int., 166, 518–528, 2006.
Hulot, G. and A. Chulliat, On the possibility of quantifying diffusion and horizontal Lorentz forces at the Earth’s core surface, Phys. Earth Planet. Inter., 135, 47–54, 2003.
Jackson, A., Time-dependency of tangentially geostrophic core surface motions, Phys. Earth Planet. Inter., 103, 293–311, 1997.
Jackson, A., C. G. Constable, M. R. Walker, and R. L. Parker, Models of Earth’s main magnetic field incorprating flux and radial vorticity constraints, Geophys. J. Int., 171, 133–144, 2007.
Jault, D. and J.-L. Le Mouël, Does secular variation involve motions in the deep core?, Phys. Earth Planet. Inter., 82, 185–193, 1994.
Le Huy, M., M. Mandea, J.-L. Le Mouël, and A. Pais, Time evolution of the fluid flow at the top of the core, Earth Planets Space, 52, 163–173, 2000.
Le Mouël, J.-L., Outer-core geostrophic flow and secular variation of Earth’s geomagnetic field, Nature, 311, 734–735, 1984.
Lesur, V., I. Wardinski, M. Rother, and M. Mandea, GRIMM: the GFZ Reference Internal Magnetic Model based on vector satellite and observatory data, Geophys. J. Int., 173, 382–394, 2008.
Lesur, V., I. Wardinski, S. Asari, B. Minchev, and M. Mandea, Modelling the Earth’s core magnetic field under flow constraints, Earth Planets Space, 62, 503–516, 2010.
Love, J. J., A critique of frozen-flux inverse modelling of a nearly steady geodynamo, Geophys. J. Int., 138, 353–365, 1999.
Mandea Alexandrescu, M., D. Gibert, J.-L. Le Mouël, G. Hulot, and G. Saracco, An estimate of average lower mantle conductivity by wavelet analysis of geomagnetic jerks, J. Geophys. Res., 104, 17735–17745, 1999.
Moon, W., Numerical evaluation of geomagnetic dynamo integrals, Comput. Phys. Commun., 16, 267–271, 1979.
O’Brien, M. S., C. G. Constable, and R. L. Parker, Frozen-flux modelling for epochs 1915 and 1980, Geophys. J. Int., 128, 434–450, 1997.
Olsen, N. and M. Mandea, Rapidly changing flows in the earth’s core, Nature Geosci., 1, 390–394, 2008.
Pais, M. A. and D. Jault, Quasi-geostrophic flows responsible for the secular variaion of the Earth’s magnetic field, Geophys. J. Int., 173, 421–443, 2008.
Pais, M. A., O. Oliveira, and F. Nogueira, Nonuniqueness of inverted core-mantle boundary flows and deviations from tangential geosgrophy, J. Geophys. Res., 109, B08105, doi:10.1029/2004JB003012, 2004.
Pinheiro, K. and A. Jackson, Can a 1-D mantle electrical conductivity model generate magnetic jerk differential time delays?, Geophys. J. Int., 173, 781–792, 2008.
Roberts, P. H. and S. Scott, On the analysis of the secular variation. I. A hydrodynamic constant: theory, J. Geomag. Geoelectr., 17, 137–151, 1965.
Sabaka, T., N. Olsen, and M. Purucker, Extending comprehensive models of the Earth’s magnetic field with Ørsted and CHAMP data, Geophys. J. Int., 159, 521–547, 2004.
Voorhies, C. V., Geomagnetic estimates of steady surficial core flow and flux diffusion: unexpected geodynamo experiments, in Dynamics of Earth’s Deep Interior and Earth Rotation, edited by Le Mouël, J.-L., D. E. Smylie, and T. Herring, vol. 72, pp. 113–125, AGU Geophysical Monograph, 1993.
Voorhies, C. V., Narrow-scale flow and a weak field by the top of earth’s core: Evidence from Ørsted, magsat, and secular variation, J. Geophys. Res., 109, doi:10.1029/2003JB002833, 2004.
Wardinski, I., R. Holme, S. Asari, and M. Mandea, The 2003 geomagnetic jerk and its relation to the core surface flows, Earth Planet. Sci. Lett., 267, 468–481, 2008.
Whaler, K. A. and R. Holme, Consistency between the flow the top of the core and the frozen-flux approximation, Earth Planets Space, 59, 1219–1229, 2007.
Acknowledgments
We thank I. Wardinski for a thorough review of the manuscript during its preparation. MM work is IPGP contribution no. 3061.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A. Description of the SV Parts in Terms of Linear Sets
A radial SV distribution  r over the CMB can be regarded as an element of a linear space M of the scalar field over a spherical surface. In a similar manner, a horizontal core flow distribution vH just below the CMB can be regarded as an element of a linear space C of the horizontal vector field over the same spherical surface. Then, Eq. (1) represents a linear mapping T: C → M, inherent to the distribution of radial MF, Br, on the spherical surface. Let Mad denote the image of T, i.e. a subset of M with its elements satisfying the FF condition (2). It is readily noticed from Eq. (1), or the condition (2), that Mad is a linear subspace. All other SV elements that do not meet the condition form a subset Mna. In this paper, the elements of the subsets Mad and Mna are referred to as ‘advective SV’ and ‘non-advective SV’, respectively.
r over the CMB can be regarded as an element of a linear space M of the scalar field over a spherical surface. In a similar manner, a horizontal core flow distribution vH just below the CMB can be regarded as an element of a linear space C of the horizontal vector field over the same spherical surface. Then, Eq. (1) represents a linear mapping T: C → M, inherent to the distribution of radial MF, Br, on the spherical surface. Let Mad denote the image of T, i.e. a subset of M with its elements satisfying the FF condition (2). It is readily noticed from Eq. (1), or the condition (2), that Mad is a linear subspace. All other SV elements that do not meet the condition form a subset Mna. In this paper, the elements of the subsets Mad and Mna are referred to as ‘advective SV’ and ‘non-advective SV’, respectively.
Under the TG assumption, the flow space is limited to its linear subspace Ctg, its elements satisfying a linear constraint (4). Then, T maps Ctg to a SV subset Mge (⊂ M) which is composed of the SV elements necessarily satisfying the FF+TG condition (let Ttg denote this particular mapping). The image Mge of Ttg is a linear subspace, as indicated by the linear properties of  r and vH in Eqs. (1) and (4), as well as by the necessary condition derived by Chulliat and Hulot (2001). All other SV elements that do not meet the condition form a subset Mng. Note that Mna ⊂ Mng ⊂ M, as the FF condition is deduced from the FF+TG condition (Chulliat and Hulot, 2001; Hulot and Chulliat, 2003). The elements of Mge and Mng are referred to as ‘geostrophic SV’ and ‘non-geostrophic SV’, respectively.
r and vH in Eqs. (1) and (4), as well as by the necessary condition derived by Chulliat and Hulot (2001). All other SV elements that do not meet the condition form a subset Mng. Note that Mna ⊂ Mng ⊂ M, as the FF condition is deduced from the FF+TG condition (Chulliat and Hulot, 2001; Hulot and Chulliat, 2003). The elements of Mge and Mng are referred to as ‘geostrophic SV’ and ‘non-geostrophic SV’, respectively.
It should be noted that the total SV space M is not a direct sum of either pair of the subsets, Mad and Mna, or Mge and Mng, as obvious from the fact that only Mad and Mge are subspaces. Accordingly, the decompositions of a given element of M into those of the subsets Mad and Mna, or Mge and Mng, are not unique. Nevertheless, it is possible to perform a unique decomposition, if one lets M be a Euclidean space giving a certain definition of scalar product, such as given by Eq. (7); according to the projection theorem, one can perform an orthogonal decomposition, uniquely dividing an element of a Euclidean space into two projections, each on a certain subspace and its orthogonal complementary space. Thus, Mna (resp. Mng) can be specified as a complement of the subspace Mad (resp. Mge) over M for the given definition of scalar product.
Elements of infinite-dimensioned spaces M and C cannot be expressed by a finite number of parameters. The SH representation of elements of M, with the truncation at degree LSV, is considered to be that of a finite-dimensioned subspace  of M. Its dimension is given by NSV (= LSV(LSV + 2)). Likewise, the expression of elements of C (resp. Ctg) truncated at degree LFL is regarded as that of the subspace
of M. Its dimension is given by NSV (= LSV(LSV + 2)). Likewise, the expression of elements of C (resp. Ctg) truncated at degree LFL is regarded as that of the subspace  of C (resp.
of C (resp.  of Ctg) with the dimension NFL (= 2LFL(LFL + 2)) (resp.
of Ctg) with the dimension NFL (= 2LFL(LFL + 2)) (resp.  ). Now the SH domain vectors of the SV coefficient bb and the flow coefficient m in Eq. (8) are the elements of finite-dimensional real vector spaces
). Now the SH domain vectors of the SV coefficient bb and the flow coefficient m in Eq. (8) are the elements of finite-dimensional real vector spaces  and
and  , which are isomorphic to the spaces
, which are isomorphic to the spaces  and
and  , respectively. In the case with the TG flow limitation, the SV coefficient vector
, respectively. In the case with the TG flow limitation, the SV coefficient vector  and TG flow coefficient vector w in Eq. (9) are the elements of
and TG flow coefficient vector w in Eq. (9) are the elements of  and
and  , which are isomorphic to
, which are isomorphic to  and
and  , respectively. Here, RN is an Euclidean space with its scalar product defined as
, respectively. Here, RN is an Euclidean space with its scalar product defined as  , where the superscript T denotes the transpose (not the mapping T) and f1, f2 ∈ RN.
, where the superscript T denotes the transpose (not the mapping T) and f1, f2 ∈ RN.
The matrix A in Eq. (8) (resp. Atg in Eq. (9)) does not represent T (resp. Ttg) completely, but only the mapping  (resp.
(resp.  ) for the finite dimensions. Of course, there can be an infinite number of matrices representing
) for the finite dimensions. Of course, there can be an infinite number of matrices representing  (resp.
(resp.  ) in accordance with the choice of basis set for the spaces
) in accordance with the choice of basis set for the spaces  (resp.
(resp.  ) and
) and  (resp.
(resp.  ). Nevertheless, the representation matrix A, for example, can be specified uniquely by appropriately selecting the basis sets such that
). Nevertheless, the representation matrix A, for example, can be specified uniquely by appropriately selecting the basis sets such that  and
and  as well as
as well as  and
and  are isomorphic also as Euclidean spaces. This relation between
are isomorphic also as Euclidean spaces. This relation between  and
and  or
or  and
and  is actually established by using the change-of-basis matrix W1/2 defined by Eq. (10).
is actually established by using the change-of-basis matrix W1/2 defined by Eq. (10).
Appendix B. Singular Value Error from Main Field Model Variance
Variances  of the singular values λi of matrix A should arise from those of the Gauss coefficients b, as all elements of A are functions of b, and so are those of its subsequent matrices
of the singular values λi of matrix A should arise from those of the Gauss coefficients b, as all elements of A are functions of b, and so are those of its subsequent matrices  , V and Λ(= diag(λi)), if not described explicitly in terms of b. As shown below, nevertheless,
, V and Λ(= diag(λi)), if not described explicitly in terms of b. As shown below, nevertheless,  can be derived simply from the variances of b, given the covariance matrix Cb about the mean values bo.
can be derived simply from the variances of b, given the covariance matrix Cb about the mean values bo.
Applying Taylor expansion about bo (e.g. A(bo + δb) = A(bo) + δA(bo) + ...) to all matrices in the equation Λ(b) =  T(b) A(b)
T(b) A(b)  (b) and disregarding O(δ2) terms, one has
(b) and disregarding O(δ2) terms, one has

The diagonal components of the first and third terms on the RHS of above equation are always zero because A is the diagonal matrix and δUT U and VTδV are off-diagonal matrices; note, for example, that the identity UT U = | is independent of b, leading to δ(UTU) = δUTU + (δUTU)T = 0. The singular value perturbations are then written as  , where ui and vi are i-th column vectors of U and V, respectively. Since one can write it also as
, where ui and vi are i-th column vectors of U and V, respectively. Since one can write it also as

using the row vector

the variance of singular value λi is derived as

where E [x] denotes the statistical expected value of x.
Rights and permissions
This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Asari, S., Lesur, V. & Mandea, M. Geomagnetic secular variation violating the frozen-flux condition at the core surface. Earth Planet Sp 62, 693–709 (2010). https://doi.org/10.5047/eps.2010.08.004
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.5047/eps.2010.08.004
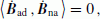

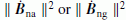 is minimum.
is minimum.
 (gray dots) of the matrix A for the MF models from (a) GRIMM (LMF = 12) at 2003.5 and (b) CM4 (LMF = 13) at 1980.0. The maximum number
(gray dots) of the matrix A for the MF models from (a) GRIMM (LMF = 12) at 2003.5 and (b) CM4 (LMF = 13) at 1980.0. The maximum number  of non-zero singular values is 1079 and 1260 for
of non-zero singular values is 1079 and 1260 for


 and
and  , for the input SV
, for the input SV 
 (gray dots) of the matrix Atg for the MF models from (a) GRIMM (LMF = 12) and (b) CM4 (LMF = 13). The maximum number
(gray dots) of the matrix Atg for the MF models from (a) GRIMM (LMF = 12) and (b) CM4 (LMF = 13). The maximum number  of non-zero singular values is 576 and 676 for GRIMM and CM4, respectively.
of non-zero singular values is 576 and 676 for GRIMM and CM4, respectively.


 and
and  , for the input SV
, for the input SV 

