Earthquake Forecast Testing Experiment in Japan (II)
- Article
- Open access
- Published:
Significant improvements of the space-time ETAS model for forecasting of accurate baseline seismicity
Earth, Planets and Space volume 63, pages 217–229 (2011)
Abstract
The space-time version of the epidemic type aftershock sequence (ETAS) model is based on the empirical laws for aftershocks, and constructed with a certain space-time function for earthquake clustering. For more accurate seismic prediction, we modify it to deal with not only anisotropic clustering but also regionally distinct characteristics of seismicity. The former needs a quasi-real-time cluster analysis that identifies the aftershock centroids and correlation coefficient of a cluster distribution. The latter needs the space-time ETAS model with location dependent parameters. Together with the Gutenberg-Richter’s magnitude-frequency law with location-dependent b-values, the elaborated model is applied for short-term, intermediate-term and long-term forecasting of baseline seismic activity.
1. Introduction
Seismicity patterns vary substantially from place to place, showing various clustering features, though some of the fundamental physical processes leading to earthquakes may be common to all events. Kanamori (1981) postulates that fault zone heterogeneity and complexity are responsible for the observed variations. Such complex features have been tackled in terms of stochastic point-process models for earthquake occurrence. The stochastic models have to be accurate enough in the sense that they are spatio-temporally well adapted to and predict various local patterns of normal activity. The epidemic type aftershock sequence (ETAS) model and its space-time extension have been introduced for such a purpose (Ogata, 1985, 1988, 1993, 1998).
However, their postulate is that the parameter values are assumed to be the same throughout the whole region and time span considered. We learn by experience that the difference of parameter values of the model at different subre-gions becomes more significant as the catalog size increases by lowering the magnitude threshold or as the area of the investigation becomes larger. For example, the p-value of the aftershock decay varies from place to place (Utsu, 1969), besides the background seismicity that obviously depends on the location. If the space-time ETAS model is fitted to such a dataset, the parameter estimates on average are obtained for the seismicity on the whole area, but they lead to biased seismicity prediction in the subregions where the seismicity pattern is significantly different from the one estimated for the whole area (see Ogata, 1988, for example).
Therefore, the best fitted case among the candidates of the space-time ETAS models in Ogata (1998) was extended to the hierarchical version of the model (the hierarchical space-time ETAS model, HIST-ETAS model in short) in which the parameters depend on the location of the earthquakes (Ogata et al., 2003; Ogata, 2004). The software package of the computing programs is in preparation for publishing (Ogata et al., 2010).
Using the present HIST-ETAS model together with Gutenberg-Richter’s magnitude frequency (Gutenberg and Richter, 1944) with the location dependent b-values, we are able to forecast the baseline seismic activity more accurately than ever, and thus we take a part in the Earthquake Forecast Testing Experiment in Japan (EFTEJ) for a short-term, intermediate-term and long-term future in and around Japan (http://www.eic.eri.u-tokyo.ac.jp/ZISINyosoku/wiki.en/wiki.cgi). This manuscript describes a sequence of procedures of pre-treatment (recompiling) of the space-time data, parameter estimation of the HIST-ETAS model as well as estimation of the location dependent b-values to undertake the short-, intermediate- and long-term forecasting.
2. Location Dependent Space-Time ETAS Model
First of all, we are concerned with statistical models for the data of occurrence times and locations of earthquakes whose magnitudes equal to or larger than a certain cut-off magnitude Mc. We define the occurrence rate λ(t, x, yǀH t ) of an earthquake at time t and the location (x, y) conditional on the past history of the occurrences, satisfying the relation

where H t = {(t i , x i , y i , M i ); t i < t} is the history of earthquake occurrence times {t i } up to time t associated with the corresponding epicenters (x i , y i ) and magnitudes {M i }. Thus a space-time probability forecast can be provided by the conditional occurrence rate function as a seis-micity model.
We would like to predict the standard short-term seismic-ity for a region A using the models of the location dependent parameters that reflect different regional and physical characteristics of the earth’s crusts. Namely, we consider a space-time ETAS model whose parameter values vary from place to place depending on the location (x,y). Consider the space-time occurrence rate conditioned on the occurrence history H t up to time t such that

where (x j , y j ) and S j are the aftershock centroid and normalized variance-covariance matrix of spatial clusters, respectively, which are specified in the next section. We are particularly concerned with the spatial estimates of the first two parameters of the model. Namely, μ(x, y) of the background seismicity is useful for long-term prediction of large earthquakes (Ogata, 2008). Also, the model with normalized aftershock productivity K(x, y) could possibly be more useful for immediate aftershock probability forecast than the one implemented in Marzocchi and Lombardi (2009), especially in the case where the anisotropic features are not neglected. The reasons and their utility of the basic structure of the model in (2) are demonstrated in Ogata (1998).
As will be specifically described in Section 5, each of the parameters μ(x, y), K (x, y), α(x, y), p(x, y) and q(x, y) is represented by a piecewise function whose value at any location (x,y) is interpolated by the three values (the coefficients) at the locations of the nearest three earthquakes (Delaunay triangle vertices) on the planed tessellated by epicenters. The coefficients of the parameter functions are simultaneously estimated by maximizing a penalized log-likelihood function that determines the optimum trade-off between the goodness of fit to the data and uniformity constraints of the functions (i.e., facets of each piecewise linear function being as flat as possible). Here, such optimum trade-off is objectively attained by minimizing the Akaike Bayesian Information Criterion (ABIC; Akaike, 1980; see Section 4) that actually evaluates the expected predictive error of Bayesian models based on the data used for the estimation (e.g., Ogata, 2004).
3. Data Processing for Anisotropic Clusters
According to the format required by the EFTEJ, we use the hypocenter catalog of the Japan Meteorological Agency (JMA) for the period 1926-2008 as the original source. Furthermore, we combine the catalog with the Utsu catalog (Utsu, 1982, 1985) for the period 1886–1925, whose magnitudes are consistent with the JMA catalog. Actually, the detection rate of smaller earthquakes is low in early period. Nevertheless, we utilize such large earthquakes as the history in the ETAS model in the precursory period because they are possibly influential to the seismicity in the target period. The accuracy of the hypocenter depth of the JMA catalogue is not satisfactory especially in offshore regions, so that we ignore the depth axis and consider only longitude and latitude for the location of an earthquake restricting ourselves to shallow events down to 100 km depth. Also, we should be sensitive to and avoid the constrained epicenters in such a way that they are subsequently located at the same place or on lattice coordinates because these cause odd or biased estimates of the space-time ETAS models.
We preprocess the data in the original JMA catalog to fit the space-time ETAS model (2) as follows. First of all, to predict a possible anisotropic spatial cluster, we utilize the data of all detected earthquakes with depths shallower than 100 km throughout whole Japan; that is, within the rectangular region bounded by 120° E and 150° E meridians, and 20°N and 50°N parallels. Then, instead of using the epicenter location in hypocenter catalogues that is the location of rupture initiation, we adopt the centroid coordinates of aftershocks for the model (2). Furthermore, we see that aftershocks are approximately elliptically distributed (Utsu, 1969) as represented by a quadratic function using the matrix S j in the model, which reflects the ratio of the length to width of the ruptured fault, its dip angle and the location errors of aftershock epicenters. To determine the matrix S j , we consider each large earthquake as a cluster parent (mainshock) that followed by enough number of clustered events (aftershocks) within a short time span (say, one hour) and within the square domain of side distance 3.33 × 100.5M−2 + 66.6 km centered at the epicenter location, taking the epicenter errors in early days into consideration (see Utsu, 1969; Ogata et al., 1995; hereafter called as the Utsu Spatial Distance). Specifically, for the cluster parents, we consider all earthquakes of M ≥ 5 for short-and intermediate-term and M ≥ 6 for long-term forecast, which are more than one unit larger than the cut-off magnitude (M 4 for short- and intermediate-term and M 5 for long-term as assigned by the EFTEJ). On the other hand, we use all earthquakes located by the JMA for the cluster members for the following analysis. Figure 1 shows several examples of such spatial clusters of earthquakes that took place within an hour.
These panels show aftershocks occurring during the first hour after the mainshock that is indicated by a star. The occurrence date and magnitude of the mainshock are printed. The AIC values of Models 0–3 relative to the largest one (see text) are listed in each panel, where the model of the smallest value is adopted for the forecast of the aftershock cluster anisotropy.
To predict whether the cluster develops in isotropy or anisotropy, we fit a bi-variate Normal distribution to the epicenter coordinates of the aftershocks in each cluster to obtain the maximum likelihood estimate of the average vector  and the covariance matrix with the elements
and the covariance matrix with the elements  and
and  for S
j
in (2) in the form
for S
j
in (2) in the form

Model 0 represents the null model with the original epicenter location with σ1 = σ2 = 1 and ρ = 0. Alternatively, the epicenter coordinates of the cluster parent is replaced by the centroid coordinates  of their immediate aftershocks (Model 1), or the identity matrix is replaced by the normalized variance-covariance matrix (Model 2), or the both are replaced (Model 3). The model of the smallest AIC value is adopted among Models 0–3. All the other events including the cluster members remain the same as the null model (Model 0); namely, the same coordinate as that of the epicenter of the original catalogue associated with the identity matrix for S
j
. This selection procedure is comparable to the projection of the centroid moment tensor solution (Dziewonski et al., 1981) to the surface.
of their immediate aftershocks (Model 1), or the identity matrix is replaced by the normalized variance-covariance matrix (Model 2), or the both are replaced (Model 3). The model of the smallest AIC value is adopted among Models 0–3. All the other events including the cluster members remain the same as the null model (Model 0); namely, the same coordinate as that of the epicenter of the original catalogue associated with the identity matrix for S
j
. This selection procedure is comparable to the projection of the centroid moment tensor solution (Dziewonski et al., 1981) to the surface.
As requested by the EFTEJ, we consider two target periods with different threshold magnitudes for the long- and short-term forecasts, taking the evolution of detection capability of earthquakes by the seismic network of the JMA. The former one is 1926–2008 with threshold magnitude M 5.0, and the latter is 2000–2008 with threshold magnitude M 4.0. These are regarded as almost completely detected throughout the respective target period and the Japan area except for the north-end off-shore and southern end of Izu-Ogasawara (Izu-Bornin) Islands in early years. We use a moderate number of large earthquakes (M 6 or larger) in the precursory period to the target period of the analysis, as the history of the ETAS model. Then, based on this earthquake data, we form the Delaunay tessellation that is necessary to apply the location dependent space-time ETAS model as specified in Section 5.
4. Optimization and Selection of Bayesian Models
We are concerned with statistical models to describe space-time heterogeneity which actually require a large number of parameters. Consider the case where such models with parameters {θ = (θ i ) ∈ Θ} are given by likelihood L(θ ǀ data). To estimate the parameters; we often use the penalized log likelihood (Good and Gaskins, 1971)

where the function Q represents a positive valued penalty function, and τ = (τ1,⋯, τ K ) is a vector of the hyper-parameters that control the strength of some constraints between the parameters θ. The crucial point here is the tuning of τ. From the Bayesian viewpoint, the penalty function is related to the prior probability density π(θǀτ) = e−Q(θǀτ)/ ∫Θe−Q(θǀτ)dθ and the exponential to the penalized log likelihood function R is proportional to the posterior function. For determining suitable values of the hyper-parameters τ, consider the posterior probability density function p(θǀdata; τ) = L(θǀdata)π(θǀτ)/Λ(τǀdata) with normalizing factor

Maximization of this normalizing factor or its logarithm with respect to the hyper-parameters τ is called the method of the Type II maximum likelihood due to Good (1965). Given a set of data, one seeks to compare the goodness-of-fit of Bayesian models that have distinct likelihoods or distinct priors and to search for the optimal hyper-parameter values. For instance, Ogata et al. (1991) compared the use of different priors for isotropic and anisotropic smoothness constraints, which need two and five hyper-parameters, respectively. For such a purpose, Akaike (1980) justified and developed the Good’s method based on the entropy maximization principle (Akaike, 1978) and defined ABIC = −2maxτ lnΛ(τǀdata) + 2dim(τ) for consistent use with the Akaike Information Criterion (AIC; Akaike, 1974). Here, dim(τ) is the number of the hyper-parameters. Both ABIC and AIC are to be minimized for the comparison of Bayesian and ordinary likelihood-based models, respectively, for better fit to the data. The normalizing factor Λ (τ ǀ data) in Eq. (4) is called the likelihood of the Bayesian model with respect to the hyper-parameters τ. The Bayes factor (e.g., O’Hagan, 1994) corresponds to the likelihood ratio of the Bayesian models.
5. Hierarchical Modelling on Tessellated Spatial Region
5.1 Delaunay interpolation functions
Consider the location-dependent space-time ETAS model where the five parameters in (2) are expressed by

Here, the constants  and
and  are baseline parameter values, and the functions ϕ1(x, y), ϕ2(x, y), ϕ3(x, y), ϕ4(x, y) and ϕ5(x, y) are expanded using sufficiently many coefficients. The exponential with respect to each ϕ-function is adopted to avoid negative values of the parameter functions. The two dimensional cubic B-spline expansion could be used as in Ogata and Katsura (1988, 1993) and Ogata et al. (1991). However, the spatial distribution of the epicenters such as shown in Fig. 2(a) appears too highly clustered for a bi-cubic spline function to represent well adapted and locally unbiased estimates of seismicity rate in such active regions. This is even more difficult for the recent data where earthquakes are accurately located.
are baseline parameter values, and the functions ϕ1(x, y), ϕ2(x, y), ϕ3(x, y), ϕ4(x, y) and ϕ5(x, y) are expanded using sufficiently many coefficients. The exponential with respect to each ϕ-function is adopted to avoid negative values of the parameter functions. The two dimensional cubic B-spline expansion could be used as in Ogata and Katsura (1988, 1993) and Ogata et al. (1991). However, the spatial distribution of the epicenters such as shown in Fig. 2(a) appears too highly clustered for a bi-cubic spline function to represent well adapted and locally unbiased estimates of seismicity rate in such active regions. This is even more difficult for the recent data where earthquakes are accurately located.
(a) Epicenter locations (dots) of earthquakes of M ≥ 4.0 in and around Japan for the target period 2000–2008 together with those of M ≥ 6.0 from the period 1885–1999 that are used as the history of the ETAS model, and (b) Delaunay tessellation connecting the epicenters and some points on the boundary.
Therefore, our alternative proposal for the present case is as follows. Consider the Delaunay triangulation (e.g., Green and Sibson, 1978); that is to say, the whole rectangular region A is tessellated by triangles with the vertex locations of earthquakes and some additional points {(x i ,y i ),i = 1,…, N + n}, where N is the number of earthquakes and n is the number of the additional points on the rectangular boundary including the corners. Here, for successfully fulfilling a Delaunay tessellation, we sometimes need very small perturbation of epicenters to avoid lattice structure or duplicated locations in a local domain. Figure 2(b) shows such a tessellation based on the epicenters of the present dataset (Fig. 2(a)) and the additional points on the boundaries.
Then, define the piecewise linear function ϕ(x, y) on the tessellated region such that its value at any location (x, y) in each triangle is linearly interpolated by the three values at the vertices. Specifically, consider a Delaunay triangle and the coordinates of its vertices (x i , y i ), i = 1, 2, 3. Then, for the values ϕ i = ϕ(x i , y i ), i = 1, 2, 3, the function value at any location inside the triangle is given as follows:
Consider the linear equations

to obtain the non-negative solution  and
and  so that we have
so that we have

Such a function suitably represents the variation of the samples on a highly non-homogeneous or clustered point pattern. That is to say, we can estimate detailed changes of rate in a region where the observations are densely populated.
5.2 Spatial ETAS with all parameters constant
Now we have to start with the simplest space-time ETAS model in which all the parameters θ = (μ, K, c, α, p, d, q) in (2) are constant throughout the whole region, equivalently, all the functions ϕ k (x, y) in (5), k = 1, 2,…, 5, are equal to zero. The maximum likelihood estimates (MLE) are obtained by the maximizing the log-likelihood function

for the earthquakes in the target period [S, T], where H t is the history of earthquake occurrences before time t including those from the precursory period [0, S]. We use a quasi-Newton method (e.g., Fletcher and Powell, 1963) for the numerical maximization. When the number of earthquakes is very large, the computing takes substantially long time due to the double sum in the first term of the log likelihood (8). One may be interested in a quicker but approximate computation by only taking the double sum of the earthquake pairs closer than a certain distance, such as 4 times of the Utsu Spatial Distance 3.33 × 100.5M−2 km (cf., Section 3). This restriction considerably lessens the required calculations because the intensity at the location of subsequent events will only be influenced by historical events if the given event is contained within the threshold distance associated with the historical events. We take this restriction for an approximation throughout the present paper although we can perform the computations without the restriction taking the longer c.p.u. time. The MLE for the datasets with magnitude thresholds M 4 and M 5 are given in Tables 1 and 2, respectively. It should be noted here that the space-time ETAS models with constant parameter including μ and K appear to provide biased estimates for other parameters (see Tables 1 and 2, and Section 7). In particular, the p-value of the models are less than 1.0 while the Bayesian models take p > 1 values as obtained below. Nevertheless, the obtained MLE are then used for the initial guess to estimate the restricted HIST-ETAS model as specified in the next section.
5.3 ETAS: Spatially varying μ and K
The obtained MLEs under the constant parameter μ for the background seismicity cause the highly biased MLEs for the baseline estimates  and
and  in (5) as well as c and d. Without appropriately unbiased initial guess of the baseline parameters, it is not easy to stably obtain the converging solution of the five location-dependent parameters in (5) due to the search in very high dimensional coefficient space. Therefore, before applying the model (2) with (5), we use the MLEs
in (5) as well as c and d. Without appropriately unbiased initial guess of the baseline parameters, it is not easy to stably obtain the converging solution of the five location-dependent parameters in (5) due to the search in very high dimensional coefficient space. Therefore, before applying the model (2) with (5), we use the MLEs  of the space-time ETAS model for the initial guess of the baseline parameters of a special version of the model (2) in which we assume that only the background rates
of the space-time ETAS model for the initial guess of the baseline parameters of a special version of the model (2) in which we assume that only the background rates  and aftershock productivity rate
and aftershock productivity rate  are location dependent; namely, other functions ϕ
k
(x, y), k = 3, 4, 5, in (5) are fixed to be zero. Hereafter we call this restricted model as μK-HIST-ETAS model. In order to estimate ϕ
k
(x,y) with each of k = 1, 2, we use more than twice as many coefficients as the number of the earthquake data.
are location dependent; namely, other functions ϕ
k
(x, y), k = 3, 4, 5, in (5) are fixed to be zero. Hereafter we call this restricted model as μK-HIST-ETAS model. In order to estimate ϕ
k
(x,y) with each of k = 1, 2, we use more than twice as many coefficients as the number of the earthquake data.
For stable estimation of such functions, we need to constrain the freedom of the coefficients toward the uniformity, or less variability, of the functions. These requirements lead us to minimize the penalized log-likelihood function (3) where ln L (θ) is the log-likelihood function in (6), Q (θ ǀτ) is a penalty function against the roughness of the ϕ-functions, and τ = (w1, w2) is a set of the weights for tuning parameters (hyper-parameters). The penalty function Q represents the strength of the constraints against the variability in the first derivative of the ϕ-functions as follows:

where the index j runs across all the Delaunay triangles with areas Δ
j
; and  and
and  is the function value of the vertex coordinate
is the function value of the vertex coordinate  and
and  , respectively.
, respectively.
The penalized log-likelihood defines a trade-off between the goodness of fit to the data and the uniformity of each function, namely, the facets of the piecewise linear function being as flat as possible. A smaller weight leads to a higher regional variability of the ϕ-functions. The optimal weights  together with the maximizing baseline parameters (
together with the maximizing baseline parameters ( , c, α, p, d, q) are obtained by a Bayesian principle of maximizing the integrated posterior function (see Appendix). Here note that the baseline parameters
, c, α, p, d, q) are obtained by a Bayesian principle of maximizing the integrated posterior function (see Appendix). Here note that the baseline parameters  are automatically determined by the zero sum constraint of the corresponding ϕ-function. This overall maximization can be eventually attained by repeating alternate procedures of the separated maximizations with respected to the parameters (coefficients) and hyper-parameters (weights) described as follows.
are automatically determined by the zero sum constraint of the corresponding ϕ-function. This overall maximization can be eventually attained by repeating alternate procedures of the separated maximizations with respected to the parameters (coefficients) and hyper-parameters (weights) described as follows.
First of all, we use the obtained MLEs  of the space-time ETAS model for the initial baseline parameter and set ϕ1 (x, y) = ϕ2(x,y) = 0 for the initial coefficients. Then, we implement the maximization of the penalized log-likelihood (3) with respect to the coefficients of the ϕ-functions (see Appendix). For the maximization, we adopt a linear search procedure in conjunction with the incomplete Cholesky conjugate gradient (ICCG) method for 2(N + n) dimensional coefficient vectors by using a suitable approximate Hessian matrix
of the space-time ETAS model for the initial baseline parameter and set ϕ1 (x, y) = ϕ2(x,y) = 0 for the initial coefficients. Then, we implement the maximization of the penalized log-likelihood (3) with respect to the coefficients of the ϕ-functions (see Appendix). For the maximization, we adopt a linear search procedure in conjunction with the incomplete Cholesky conjugate gradient (ICCG) method for 2(N + n) dimensional coefficient vectors by using a suitable approximate Hessian matrix (see Appendix), where N is the number of earthquakes and n is the number of the additional points on the rectangular boundary including the corners (see Fig. 2(b)). This makes the convergence very rapid regardless of the high dimensionality of θ if the Gaussian approximations for the posterior function are adequate.
(see Appendix), where N is the number of earthquakes and n is the number of the additional points on the rectangular boundary including the corners (see Fig. 2(b)). This makes the convergence very rapid regardless of the high dimensionality of θ if the Gaussian approximations for the posterior function are adequate.
Having attained such convergences for given hyper-parameters τ = (w1, w2, c, α, p, d, q), we eventually need to perform the maximization of Λ (τ) defined in (4) with respect to τ by a direct search such as the simplex method in the 7 dimensional space. Such double optimizations are repeated in turn until the latter maximization converges. The whole optimization procedure usually converges when initial vector values for τ are set in such a way that the penalty is effective enough; otherwise, it may take very many steps to reach the solution. After all, assuming unimodality of the posterior function, one can get the optimal maximum posterior solution  for the maximum likelihood estimate
for the maximum likelihood estimate .
.
5.4 ETAS: Spatial variation in 5 parameters
Having obtained the optimal weights  with coefficients of
with coefficients of  and
and  as well as the baseline parameters
as well as the baseline parameters in the μK-HIST-ETAS model, we use these initial inputs to stably estimate the HIST-ETAS model in (2) with five location-dependent parameters in (5) by the same optimization procedure as stated above. Specifically, we first set the initial estimates
in the μK-HIST-ETAS model, we use these initial inputs to stably estimate the HIST-ETAS model in (2) with five location-dependent parameters in (5) by the same optimization procedure as stated above. Specifically, we first set the initial estimates  and
and  obtained in the above and also set ϕ3(x, y) = ϕ4(x, y) = ϕ5(x, y) = 0 with the baseline values
obtained in the above and also set ϕ3(x, y) = ϕ4(x, y) = ϕ5(x, y) = 0 with the baseline values  and
and  of the μK-HIST-ETAS model that are obtained by the above-stated procedure. Then, we consider the penalized log-likelihood function (3) with the extended penalty function
of the μK-HIST-ETAS model that are obtained by the above-stated procedure. Then, we consider the penalized log-likelihood function (3) with the extended penalty function

of τ = (w1,…, w5). Here, the baseline values  and
and  are fixed throughout the region and period. The optimal weights
are fixed throughout the region and period. The optimal weights  are obtained by the similar procedure of maximizing the integrated posterior function (see Appendix) to the procedure that has applied to the μK-HIST-ETAS model in Section 5.3. This maximization can attain sequentially and alternately as follows. First, we implement the maximization of the penalized log-likelihood (3) with respect to the coefficients of the ϕ-functions (see Appendix). For the calculation, we adopt a linear search using the incomplete Cholesky conjugate gradient (ICCG) method for 5(N + n) dimensional coefficient vectors, where N + n is the same number as given in Section 5.3. Alternately, we implement the simplex algorithm in the 5-dimensional space of
are obtained by the similar procedure of maximizing the integrated posterior function (see Appendix) to the procedure that has applied to the μK-HIST-ETAS model in Section 5.3. This maximization can attain sequentially and alternately as follows. First, we implement the maximization of the penalized log-likelihood (3) with respect to the coefficients of the ϕ-functions (see Appendix). For the calculation, we adopt a linear search using the incomplete Cholesky conjugate gradient (ICCG) method for 5(N + n) dimensional coefficient vectors, where N + n is the same number as given in Section 5.3. Alternately, we implement the simplex algorithm in the 5-dimensional space of  to maximize Λ (τ) up until this converges. Here, before the 5-dimensional simplex search, we recommend to firstly make the lattice search of (w3, w4, w5) in the logarithmic orders, such as (10i, 10j, 10k) for possible sets of integers i, j and k to compare the respective ABIC values h, while (w1, w2) remain fixed to
to maximize Λ (τ) up until this converges. Here, before the 5-dimensional simplex search, we recommend to firstly make the lattice search of (w3, w4, w5) in the logarithmic orders, such as (10i, 10j, 10k) for possible sets of integers i, j and k to compare the respective ABIC values h, while (w1, w2) remain fixed to  obtained in Section 5.3. It is a limitation of this procedure that this maximization may not converge for small sets of integers because the convergence relies on the quadratic approximation penalized log likelihood (see Appendix and the ICCG method). From our experience, 2 or 3 or larger can be a choice of the start. Then, using the set of weights with the smallest ABIC value, we can implement the 3 dimensional simplex search of (w3, w4, w5) or even the 5 dimensional simplex search of (w1, w2, w3, w4, w5) for global minimization. Here it is important to make use of the previously converged solutions of parameters (coefficients) for the next initial parameters of such large dimensions.
obtained in Section 5.3. It is a limitation of this procedure that this maximization may not converge for small sets of integers because the convergence relies on the quadratic approximation penalized log likelihood (see Appendix and the ICCG method). From our experience, 2 or 3 or larger can be a choice of the start. Then, using the set of weights with the smallest ABIC value, we can implement the 3 dimensional simplex search of (w3, w4, w5) or even the 5 dimensional simplex search of (w1, w2, w3, w4, w5) for global minimization. Here it is important to make use of the previously converged solutions of parameters (coefficients) for the next initial parameters of such large dimensions.
It is also useful to examine whether or not the characteristic parameters, particularly  and
and  are significantly uniform (i.e., spatially invariant). For this we can calculate the Akaike Bayesian Information Criterion (ABIC; see Appendix) as a byproduct of the above simplex optimization. A model with a smaller ABIC value indicates a better fit. For example, we can compare the ABIC values of the HIST-ETAS model for the optimal weights
are significantly uniform (i.e., spatially invariant). For this we can calculate the Akaike Bayesian Information Criterion (ABIC; see Appendix) as a byproduct of the above simplex optimization. A model with a smaller ABIC value indicates a better fit. For example, we can compare the ABIC values of the HIST-ETAS model for the optimal weights  with the one for (
with the one for ( , 108) to examine whether q-value is location dependent or not.
, 108) to examine whether q-value is location dependent or not.
Figures 3 with Table 1 and 4 with Table 2 provide the optimal estimates of HIST-ETAS model applied to the processed JMA data in Section 3 for the target period of 2000–2008 with threshold magnitude M 4.0, and the data for 1926–2008 with threshold magnitude M 5.0, respectively.
Maximum posterior estimates of respective parameter functions (see text) of the hierarchical space-time ETAS model and b-values of the G-R frequency that are applied to the reprocessed JMA data (see Section 3) with earthquakes of M 4.0 or larger during the target period from 2000–2008; in addition, we use earthquakes of M 6.0 or larger from the precursory period of 1885–1999 as the occurrence history of the space-time ETAS model. The colors represent the estimated coefficient values of the parameter functions μ,K, α, p,q and b-values. The dimension of μ and K is the number of events per degree per day.
The estimated images of the corresponding parameters between Figs. 3 and 4 appear similar to each other in spite of the different target periods and different cutoff magnitudes. Although the considered earthquakes with the cutoff magnitudes are mostly complete, the q-value images in both Figs. 3 and 4 shows apparent artificial feature. Namely, the inverse power q-values for distances between a mainshock and its aftershocks are lower in the margin of Japan islands than those in the interior region. This seems to be attributed to the difference of epicenter location accuracies in the land and the margin. The images of the other parameters seem to be genuine except in the very margin of the region such as in Taiwan and in the southern part of the Ogasawara islands due to the magnitude incompleteness there. Incidentally, we can obtain contour images and color images on the lattice of these parameters covering the whole area by the interpolation (7) of the Delaunay triangles such as shown in Ogata et al. (2003) and Ogata (2004).
Maximum posterior estimates of respective parameter functions of the hierarchical space-time ETAS model and b-values, applied to the reprocessed JMA data with earthquakes of M 5.0 or larger during the period of 1926–2008; in addition, we use earthquakes of M 6.0 or larger from the precursory period from 1885–1925 as the occurrence history of the ETAS model. See Fig. 3 for the additional caption.
6. Modeling the Spatially Varying b-Values
We further consider that the b-value of the Gutenberg-Richter’s magnitude frequency law is location dependent. Historically, based on the moment method, Utsu (1965) proposed the estimator  for the observation of magnitude sequence {M
i
, i = 1,…, N} where Mc is the lowest bound of the magnitudes above which almost all the earthquakes are detected. This is modified by Utsu (1970) to replace Mc by Mc − 0.05 for the unbiased estimate of the b-values in case when the given magnitudes are rounded into values with 0.1 unit, and hereafter we follow this modification for the JMA catalog.
for the observation of magnitude sequence {M
i
, i = 1,…, N} where Mc is the lowest bound of the magnitudes above which almost all the earthquakes are detected. This is modified by Utsu (1970) to replace Mc by Mc − 0.05 for the unbiased estimate of the b-values in case when the given magnitudes are rounded into values with 0.1 unit, and hereafter we follow this modification for the JMA catalog.
Aki (1965) showed that the Utsu’s b-estimator is nothing but the maximum likelihood estimate (MLE) that maximizes the likelihood function  , M
i
> Mc and β = bln 10. Wiemer and Wyss (1997) uses the MLE in ZMAP software to obtain the location dependent b-values using data from moving disk whose radius is adjusted to include the same number of earthquakes. However there remain the issues of optimal selection of the number of earthquakes in the disk and evaluation of significance of the b-value changes.
, M
i
> Mc and β = bln 10. Wiemer and Wyss (1997) uses the MLE in ZMAP software to obtain the location dependent b-values using data from moving disk whose radius is adjusted to include the same number of earthquakes. However there remain the issues of optimal selection of the number of earthquakes in the disk and evaluation of significance of the b-value changes.
We would like to solve these problems by the Bayesian procedure. Here, we assume that the b-value, or coefficient of the exponential distribution of magnitude, is dependent on the location in such a way that β θ (x, y) = b θ (x, y) ln 10 where θ is a parameter vector characterizing the function (Ogata et al., 1991). Then, having observed the magnitude data M i for each hypocenter’s coordinates (x i , y i ) with i = 1,2,…, N, the current likelihood function of θ can be written by

for M
i
> Mc. Since β, or b, is positive valued, we make the re-parameterization of the function  , so that the estimate of the b-values in space is given by
, so that the estimate of the b-values in space is given by  , where the ϕ-function is the piecewise linear on Delaunay tessellation, as given above. For a set of clusters of earthquakes, the Delaunay-based function fits better than the bi-cubic B-spline function that was used in Ogata et al. (1991). The estimation of the coefficients is undertaken by the penalized log-likelihood, where the penalty is tuned by the similar Bayesian procedure based on the ABIC (see Section 4 and Appendix). The last panels in Figs. 3 and 4 together with Table 3 provide the optimal estimates of the b-values applied to the data for the period of 2000–2008 with cutoff magnitude Mc = 3.95, and the one for 1926–2008 with cutoff magnitude Mc = 4.95, respectively. This appears similar on the whole to each other.
, where the ϕ-function is the piecewise linear on Delaunay tessellation, as given above. For a set of clusters of earthquakes, the Delaunay-based function fits better than the bi-cubic B-spline function that was used in Ogata et al. (1991). The estimation of the coefficients is undertaken by the penalized log-likelihood, where the penalty is tuned by the similar Bayesian procedure based on the ABIC (see Section 4 and Appendix). The last panels in Figs. 3 and 4 together with Table 3 provide the optimal estimates of the b-values applied to the data for the period of 2000–2008 with cutoff magnitude Mc = 3.95, and the one for 1926–2008 with cutoff magnitude Mc = 4.95, respectively. This appears similar on the whole to each other.
7. Implications of Tables and Figures
We can compare the AIC and ABIC values among the MLE based models and among the Bayesian models, respectively, although we cannot directly compare the AIC value with ABIC values here because we did not adjust the difference in the normalization factors between AIC and ABIC in the considered models. By the entropy concept from which both AIC and ABIC (Akaike, 1974, 1978, 1980) are derived, we can expect a better forecast among the MLE-based models or among the Bayesian models with a smaller AIC or ABIC, respectively, under the assumption that the stochastic structure of future seismicity will not change from the past as the baseline seismicity.
Thus, Tables 1 and 2 imply several consequences of the present fitting of the models. First, we can say that the fit of the models to the data from the target period associated with the occurrence history of large earthquakes in precursory period will forecast better than those applied to the data during the target period only. Second, the models that take the anisotropic clusters into consideration will forecast better than the models with isotropic clusters only using the original JMA hypocenter data. Third, the five parameter HIST-ETAS models will forecast better than the μK-HIST-ETAS models. Eventually, we expect the best forecasting performance by the 5 parameter HIST-ETAS models that take account of the anisotropic clustering and effect of the history in the precursory periods. Finally, the p < 1 estimate for the uniform background rate μ in space become p > 1 by the location dependent μ estimate. The reason of the p < 1 estimate is that as a compensation of the spatially uniform back ground rate, the time evolution with heavier tailed aftershock decay is easier for the spatial seismicity to concentrate in the active regions.
Figure 5 shows the pair plots between the parameter values of the HIST-ETAS model in addition to the b-value at the same location. First, each parameter of the HIST-ETAS model seems to have little correlation with the b-value. The correlations among the HIST-ETAS parameters are not clear on the whole. It may not make sense to see the correlations throughout the entire Japan region unlike the cases in Guo and Ogata (1996) in which only aftershock sequences are compared among the classified locations of inter- and intra-plate mainshocks. Nevertheless, we may see a weak correlation between μ and K parameters on a logarithmic scale. This is consistent with the observation that the asperity regions and mainshocks are complementary to the regions of high intensity of aftershock productivity (Ogata, 2004, 2008).
Plots of the pairs of parameter values in Figs. 3 and 4 (except for the q-values) at the corresponding locations. The panels in the upper triangle panels (black dots) and the lower triangle panels (gray dots) are from Fig. 3 (M ≥ 4.0) and Fig. 4 (M ≥ 5.0), respectively. The parameters μ and K are on a logarithmic scale while the others are on a linear scale.
8. Forecasting
8.1 Short-term forecast
For the short-term forecast, we first reprocess the JMA data in real time as described in Section 3. Namely, during a certain time span (say, one hour) immediately after a large earthquake, the cluster analysis is automatically implemented while during the same period, we can only to make a real time forecast using the generic (null hypothesis model) procedure with the original JMA epicenter coordinates and the identity matrix for isotropic clustering.
Then the short-term probability forecast is calculated by the joint distribution of the combination given by

where the spatial values of both ETAS coefficient and b-values at any location (x, y) can be obtained by solving the relation in (6) and then interpolated by (7). Incidentally, since the CSEP testing centers, including the EFTEJ, commonly ask us to submit the forecasting probability at each voxel [t, t + A t ) [x, x + A x ) × [y, y + A y ) × [M, M + ΔM) of sizes in time (Δ t = 1 day), space (Δ x = Δ y = 0.1 degree) and magnitude (ΔM = 0.1 magnitude unit). Therefore, we forecast the probability for such a unit time-space-magnitude volume (voxel) by

8.2 Intermediate-term forecast
Suppose that the current time is S, and we forecast the probability during the period till the time T. For a intermediate period [S, T], we forecast probability for each space-magnitude voxel by

where Λ(S,T; x, y) is obtained by the following procedure: (i) calculate the intensity λ(t,x,yǀH
S
) conditioned on the history H
S
up to time S from the HIST-ETAS model; (ii) integrate  over the time span [S, T]; (iii) normalize this by its spatial integration over the whole region; and (iv) multiply this by the average number of earthquakes of M ≥ Mc for the period of the time length T − S. Here the normalization and multiplication in steps (iii) and (iv) are necessary to modify the bias of the forecasting probability because no possible events for the history H
t
, S < t < T, in the integration step (ii) is taken into consideration in the conditional intensity function during the period [S, T].
over the time span [S, T]; (iii) normalize this by its spatial integration over the whole region; and (iv) multiply this by the average number of earthquakes of M ≥ Mc for the period of the time length T − S. Here the normalization and multiplication in steps (iii) and (iv) are necessary to modify the bias of the forecasting probability because no possible events for the history H
t
, S < t < T, in the integration step (ii) is taken into consideration in the conditional intensity function during the period [S, T].
8.3 Long-term forecast
During the period [S, T] for a sufficiently large time span T − S, λ(t, x, yǀH S ) is essentially equal to the background seismicity rate μ(x, y) for any location and time. Therefore, the intermediate-term probability above should take a very similar value for the case where we use the background seismicity rate μ(x, y) in place of λ(t, x, yǀH S ) in the above-stated procedure (i)–(iv). Thus, we adopt this as the probability of the long-term forecast of each space-magnitude voxel per unit time.
Relevantly, Ogata (2008) argues that the background rate appears better long-term forecasting for large earthquakes (M ≥ 6.7,15 years period) than the ordinary average occurrence intensity in space, by the retrospective prediction performance. This is mainly because such large earthquakes mostly occurred at the complementary regions of high K-values (e.g., Ogata, 2004) that substantially contribute to the total intensity λ(t,x,yǀH S ).
9. Concluding Remarks
We applied the hierarchical space-time ETAS (HIST-ETAS) model to the short-, intermediate- and long-term forecast of baseline seismicity in and around Japan. Each parameter of the space-time ETAS model is described by a two dimensional piecewise function whose value at a location is interpolated by the three values at the location of the nearest three earthquakes (Delaunay triangle vertices) on the tessellated plane. Such modeling by using Delaunay tessellation is suited for the observation on highly clustered points with accurate locations, and therefore we can expect locally unbiased probability evaluation there. We are particularly concerned with the spatial estimates of the first two parameters of the space-time ETAS model: namely, μ-values of the background seismicity and aftershock productivity K-values. The former is useful for the long-term prediction of the large earthquakes, and the latter for the short-term aftershock probability forecast immediately after a large earthquake.
It is noteworthy here that there is an extended version from the original space-time ETAS model with the same structure as the HIST-ETAS in (2). It is described such that

using the additional parameter γ (see Ogata and Zhuang, 2006; Zhuang et al., 2005). In principle, we can further extend this to the case where the parameter γ is also location dependent in addition to the five parameters in (5). Although it becomes unstable to obtain the estimates of the 6 location-dependent parameters mainly because of the strong correlation between the parameters α and γ, this could be a challenging task for a better forecasting.
For the joint probability of space-time-magnitude forecast, we have assumed that the sequences of magnitudes are independent from history of the occurrence times while the reverse relation is highly dependent as described by the ETAS model. Furthermore, we have adopted the exponential distribution (Gutenberg-Richter law) for the magnitude frequency. However, I believe these postulates are not always the case. Indeed, the magnitude sequence of the global large earthquakes is not at all independent between them but possesses a long-range autocorrelations (Ogata and Abe, 1989). Furthermore, Ogata (1989) considered a model for magnitude sequence where the b-value varies in time based on both history of magnitudes and occurrence times of earthquakes. Furthermore, we know that magnitude frequency in a local area is not necessarily exponentially distributed as we see in many swarm activity. These anomalies may provide some hints for a better prediction of large earthquakes than the present models for baseline seismicity.
References
Akaike, H., A new look at the statistical model identification, IEEE Trans. Autom. Control, AC-19, 716–723, 1974.
Akaike, H., A new look at the Bayes procedure, Biometrika, 65, 53–59, 1978.
Akaike, H., Likelihood and Bayes procedure, in Bayesian Statistics, edited by J. M. Bernard et al., 1–13, Univ. Press, Valencia, Spain, 1980.
Aki, K., Maximum likelihood estimate of b in the formula log N = a−bM and its confidence limits, Bull. Earthq. Res. Inst., 43, 237–239, 1965.
Dziewonski, A. M., T. A. Chou, and J. H. Woodhouse, Determination of earthquake source parameters from waveform data for studies of global and regional seismicity, J. Geophys. Res., 86, 2825–2852, 1981.
Fletcher, R. and M. J. D. Powell, A rapidly convergent descent method for minimization, Comput. J., 6, 163–168, 1963.
Good, I. J., The Estimation of Probabilities, M. I. T. Press, Cambridge, Massachusetts, 1965.
Good, I. J. and R. A. Gaskins, Nonparametric roughness penalties for probability densities, Biometrika, 58, 255–277, 1971.
Green, P. J. and R. Sibson, Computing Dirichlet tessellation in the plane, Comput. J., 21, 168–173, 1978.
Guo, Z. and Y. Ogata, Statistical relations between the parameters of aftershocks in time, space and magnitude, J. Geophys. Res., 102, 2857–2873, 1996.
Gutenberg, R. and C. F. Richter, Frequency of earthquakes in California, Bull. Seismol. Soc. Am., 34, 185–188, 1944.
Kanamori, H., The nature of seismicity patterns before large earthquakes, in Earthquake Prediction, Maurice Ewing Series, 4, edited by D. Simpson and P. Richards, 1-19, AGU, Washington D.C., 1981.
Kowalik, J. and M. R. Osborne, Methods for Unconstrained Optimization Problems, American Elsevier, New York, 1968.
Marzocchi, W. and A. M. Lombardi, Real-time forecasting following a damaging earthquake, Geophys. Res. Lett., 36, L21302, doi:10. 1029/2009GL040233, 2009.
Mori, M., FORTRAN 77 Numerical Analysis Programming, 342pp., Iwanami Publisher, Tokyo, 1986 (in Japanese).
Murata, Y., Estimation of optimum surface density distribution only from gravitational data: an objective Bayesian approach, J. Geophys. Res., 98, 12097–12109, 1992.
Ogata, Y., Statistical models for earthquake occurrences and residual analysis for point processes, Research Memorandum, No. 288, The Institute of Statistical Mathematics, Tokyo, http://www.ism.ac.jp/editsec/resmemo/resm-j/resm-2j.htm, 1985.
Ogata, Y., Statistical models for earthquake occurrences and residual analysis for point processes, J. Am. Statist. Assoc., 83, 9–27, 1988.
Ogata, Y., Statistical model for standard seismicity and detection of anomalies by residual analysis, Tectonophysics, 169, 159–174, 1989.
Ogata, Y., Space-time modelling of earthquake occurrences, Bull. Int. Statist. Inst., 55, Book 2, 249–250, 1993.
Ogata, Y., Space-time point-process models for earthquake occurrences, Ann. Inst. Statist. Math., 50, 379–402, 1998.
Ogata, Y., Space-time model for regional seismicity and detection of crustal stress changes, J. Geophys. Res., 109(B3), B03308, doi:10. 1029/2003JB002621, 2004.
Ogata, Y., Occurrence of the large earthquakes during 1978~2007 compared with the selected seismicity zones by the Coordinating Committee of Earthquake Prediction, Rep. Coord. Comm. Earthq. Predict., 79, 623–625, 2008 (in Japanese).
Ogata, Y. and K. Abe, Some statistical features of the long term variation of the global and regional seismic activity, Int. Statist. Rev., 59, 139–161, 1989.
Ogata, Y. and K. Katsura, Likelihood analysis of spatial inhomogeneity for marked point patterns, Ann. Inst. Statist. Math., 40, 29–39, 1988.
Ogata, Y. and K. Katsura, Analysis of temporal and spatial heterogeneity of magnitude frequency distribution inferred from earthquake catalogues, Geophys. J. Int., 113, 727–738, 1993.
Ogata, Y. and J. Zhuang, Space-time ETAS models and an improved extension, Tectonophysics, 413, 13–23, 2006.
Ogata, Y., M. Imoto, and K. Katsura, 3-D spatial variation of b-values of magnitude-frequency distribution beneath the Kanto District, Japan, Geophys. J. Int., 104, 135–146, 1991.
Ogata, Y., T. Utsu, and K. Katsura, Statistical features of foreshocks in comparison with other earthquake clusters, Geophys. J. Int., 121, 233–254, 1995.
Ogata, Y., K. Katsura, N. Keiding, C. Holst, and A. Green, Empirical Bayes age-period-cohort analysis of retrospective incidence data, Scand. J. Statist., 27, 415–432, 2000.
Ogata, Y., K. Katsura, and M. Tanemura, Modelling heterogeneous space-time occurrences of earthquakes and its residual analysis, Appl. Statist., 52, 499–509, 2003.
Ogata, Y., K. Katsura, D. Harte, J. Zhuang, and M. Tanemura, Spatial ETAS Program Documentation, in Computer Science Monograph, The Institute of Statistical Mathematics, Tokyo, 2011 (in preparation).
O’Hagan, A., Kendall’s Advanced Theory of Statistics, 2B, Bayesian Inference, 330 pp., Edward Arnold, London, 1994.
Utsu, T., A method for determining the value of b in a formula log n = a − bM showing the magnitude frequency relation for earthquakes, Geophys. Bull. Hokkaido Univ., 13, 99–103, 1965 (in Japanese).
Utsu, T., Aftershocks and earthquake statistics (I): some parameters which characterize an aftershock sequence and their interaction, J. Faculty Sci., Hokkaido Univ., Ser VII (geophysics), 3, 129–195, 1969.
Utsu, T., Aftershocks and earthquake statistics (II): Further investigation of aftershocks and other earthquake sequences based on a new classification of earthquake sequences, J. Faculty Sci., Hokkaido Univ., Ser VII (geophysics), 3, 198–266, 1970.
Utsu, T., Catalog of large earthquakes in the region of Japan from 1885 through 1980, Bull. Earthq. Res. Inst., Univ. Tokyo, 57, 401–463, 1982.
Utsu, T., Catalog of large earthquakes in the region of Japan from 1885 through 1980: Correction and supplement, Bull. Earthq. Res. Inst., Univ. Tokyo, 60, 639–642, 1985.
Wiemer, S. and M. Wyss, Mapping the frequency-magnitude distribution in Asperities: An improved technique to calculate recurrence times?, J. Geophys. Res., 102, 15,115–15,128, 1997.
Zhuang, J., C. Chang, Y. Ogata, and Y. Chen, A study on the background and clustering seismicity in the Taiwan region by using point process models, J. Geophys. Res., 110(B5), B05S18, doi:10. 1029/2004JB003157, 2005.
Acknowledgments
I am very grateful to Koichi Katsura and Jiancang Zhuang for their technical assistances. Comments by Annie Chu, Rick Schoenberg and the anonymous referee were useful clarications. We have used hypocenter data provided by the JMA. This study is partly supported by the Japan Society for the Promotion of Science under Grant-in-Aid for Scientifc Research no. 20240027, and by the 2010 projects of the Institute of Statistical Mathematics and the Research Organization of Information and Systems at the Transdisciplinary Research Integration Center, Inter-University Research Institute Corporation.
Author information
Authors and Affiliations
Corresponding author
Appendix A. Computations of Bayesian Models through Gaussian Approximations
Appendix A. Computations of Bayesian Models through Gaussian Approximations
We are concerned here with the technical procedure to find the optimal weights  in the penalized log-likelihood (3) with the penalty function (9) and also to find the optimal weights
in the penalized log-likelihood (3) with the penalty function (9) and also to find the optimal weights  in the similar form of the penalized log-likelihood in (3) with the penalty function Q in (9). For this purpose, we adopt a Bayesian procedure where the normalized function of exp(−Q) represents a prior density, denoted by π(θǀτ). Since the penalty function in (9) and (10) have a quadratic form with respect to the parameters θ, the prior density is of a multivariate normal distribution, in which the variance-covariance matrix is the inverse of the Hessian matrix HQ consisting of the elements of the negative second order partial derivatives of the penalty function Q. Actually, the Hessian matrix in the present case is a block diagonal matrix of five sub-matrices corresponding to each ϕ
k
-function in (5) such that
in the similar form of the penalized log-likelihood in (3) with the penalty function Q in (9). For this purpose, we adopt a Bayesian procedure where the normalized function of exp(−Q) represents a prior density, denoted by π(θǀτ). Since the penalty function in (9) and (10) have a quadratic form with respect to the parameters θ, the prior density is of a multivariate normal distribution, in which the variance-covariance matrix is the inverse of the Hessian matrix HQ consisting of the elements of the negative second order partial derivatives of the penalty function Q. Actually, the Hessian matrix in the present case is a block diagonal matrix of five sub-matrices corresponding to each ϕ
k
-function in (5) such that since we do not assume any restrictions a priori between the different ϕ
k
-functions. Here, all sub-matrices of
since we do not assume any restrictions a priori between the different ϕ
k
-functions. Here, all sub-matrices of  are sparse and have the same configuration of non-zero elements; specifically, the (i, j) -element is non-zero if and only if the pair of points i and j are vertices of the same Delaunay triangle.
are sparse and have the same configuration of non-zero elements; specifically, the (i, j) -element is non-zero if and only if the pair of points i and j are vertices of the same Delaunay triangle.
Then, for the fixed maximizing hyper-parameters  , the maximized solution
, the maximized solution  of the penalized log-likelihood in (3) is nothing but the optimal maximum posterior estimate, i.e., the mode of the posterior density.
of the penalized log-likelihood in (3) is nothing but the optimal maximum posterior estimate, i.e., the mode of the posterior density.
However, the integration of the posterior function in (4) cannot be analytically carried out since the likelihood function of the point-process model is not normally distributed. Nevertheless, by virtue of the normal prior distribution, normal approximation of the posterior function is useful. That is to say, the penalized log-likelihood is well approximated by the quadratic form

where  , and H
T
(θǀτ) is the Hessian matrix of T (θǀτ) consisting of its negative second-order partial derivatives with respect to θ.
, and H
T
(θǀτ) is the Hessian matrix of T (θǀτ) consisting of its negative second-order partial derivatives with respect to θ.
We further assume that the Hessian matrix in (A.1) is well approximated by a block diagonal matrix of five sub-matrices,  . Namely, we assume independency between the coefficients of the different ϕ
k
-functions in the penalized log-likelihood (3). Thus, the log-likelihood of the present Bayesian model is given by
. Namely, we assume independency between the coefficients of the different ϕ
k
-functions in the penalized log-likelihood (3). Thus, the log-likelihood of the present Bayesian model is given by

where H R and H Q is the block diagonal Hessian matrix of the function R and Q in (3), respectively, and ‘det{.}’ indicates the determinant of the matrices.
To compute the optimal hyper-parameters, we repeat the following steps of (A)–(D):
-
(A)
For a given τ being fixed, set the gradient of the penalized log-likelihood, u = ∂T/∂θ at an initial parameter θ0.
-
(B)
Maximize T in (A.1) with respect to θ that is on the one-dimensional straight line determined by the initial parameter vector θ0 and the gradient vector u (Linear Search; e.g., Kowalik and Osborne, 1968).
-
(C)
Replace the maximizing parameter
 in step (B) by θ0. Then, compute the gradient vector u0 = ∂T/∂θ at θ0. Solve the equation H
T
u = u0 by the Incomplete Cholesky Conjugate Gradient (ICCG) method (e.g., Mori, 1986) to get the vector u for the direction of the next Linear Search in step (B) until the function T attains the maximum overall θ, which is the maximum posterior (MAP) solution for the given τ.
in step (B) by θ0. Then, compute the gradient vector u0 = ∂T/∂θ at θ0. Solve the equation H
T
u = u0 by the Incomplete Cholesky Conjugate Gradient (ICCG) method (e.g., Mori, 1986) to get the vector u for the direction of the next Linear Search in step (B) until the function T attains the maximum overall θ, which is the maximum posterior (MAP) solution for the given τ. -
(D)
Calculate log Λ (τ) using the quadratic approximation in (A.1) around the MAP
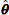 , and go to step (A) with the other τ to maximize log Λ (τ) by the direct-search maximizing method such as the simplex method (e.g., Kowalik and Osborne, 1968; Murata, 1992). The steps (A)–(D) are repeated in turn until log Λ(τ)converges. According to my experience, the convergence rate in step (C) is very fast in spite of the very high dimensionality of θ. This is expected when the quadratic approximations of T are adequate for a region around the MAP solution
, and go to step (A) with the other τ to maximize log Λ (τ) by the direct-search maximizing method such as the simplex method (e.g., Kowalik and Osborne, 1968; Murata, 1992). The steps (A)–(D) are repeated in turn until log Λ(τ)converges. According to my experience, the convergence rate in step (C) is very fast in spite of the very high dimensionality of θ. This is expected when the quadratic approximations of T are adequate for a region around the MAP solution 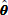 . After all, assuming a uni-modal posterior function, we can get the optimal MAP solution for the maximum likelihood estimate
. After all, assuming a uni-modal posterior function, we can get the optimal MAP solution for the maximum likelihood estimate  of the hyper-parameters. The reader is referred to Ogata and Katsura (1988, 1993) and Ogata et al. (1991, 2000, 2011), which also describe some computational details and related references therein.
of the hyper-parameters. The reader is referred to Ogata and Katsura (1988, 1993) and Ogata et al. (1991, 2000, 2011), which also describe some computational details and related references therein.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ogata, Y. Significant improvements of the space-time ETAS model for forecasting of accurate baseline seismicity. Earth Planet Sp 63, 217–229 (2011). https://doi.org/10.5047/eps.2010.09.001
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.5047/eps.2010.09.001





 in step (B) by θ0. Then, compute the gradient vector u0 = ∂T/∂θ at θ0. Solve the equation H
T
u = u0 by the Incomplete Cholesky Conjugate Gradient (ICCG) method (e.g.,
in step (B) by θ0. Then, compute the gradient vector u0 = ∂T/∂θ at θ0. Solve the equation H
T
u = u0 by the Incomplete Cholesky Conjugate Gradient (ICCG) method (e.g., 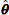 , and go to step (A) with the other τ to maximize log Λ (τ) by the direct-search maximizing method such as the simplex method (e.g.,
, and go to step (A) with the other τ to maximize log Λ (τ) by the direct-search maximizing method such as the simplex method (e.g., 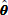 . After all, assuming a uni-modal posterior function, we can get the optimal MAP solution for the maximum likelihood estimate
. After all, assuming a uni-modal posterior function, we can get the optimal MAP solution for the maximum likelihood estimate  of the hyper-parameters. The reader is referred to
of the hyper-parameters. The reader is referred to