- Full paper
- Open access
- Published:
Dynamic precise orbit determination of Hayabusa2 using laser altimeter (LIDAR) and image tracking data sets
Earth, Planets and Space volume 72, Article number: 85 (2020)
Abstract
The precise orbit of the Hayabusa2 spacecraft with respect to asteroid Ryugu is dynamically determined using the data sets collected by the spacecraft’s onboard laser altimeter (LIght Detection And Ranging, LIDAR) and automated image tracking (AIT). The LIDAR range data and the AIT angular data play complementary roles because LIDAR is sensitive to the line-of-sight direction from Hayabusa2 to Ryugu, while the AIT is sensitive to the directions perpendicular to it. Using LIDAR and AIT, all six components of the initial state vector can be derived stably, which is difficult to achieve using only LIDAR or AIT. The coefficient of solar radiation pressure (SRP) of the Hayabusa2 spacecraft and standard gravitational parameter (GM) of Ryugu can also be estimated in the orbit determination process, by combining multiple orbit arcs at various altitudes. In the process of orbit determination, the Ryugu-fixed coordinate of the center of the LIDAR spot is determined by fitting the range data geometrically to the topography of Ryugu using the Markov Chain Monte Carlo method. Such an approach is effective for realizing the rapid convergence of the solution. The root mean squares of the residuals of the observed minus computed values of the range and brightness-centroid direction of the image are 1.36 m and 0.0270°, respectively. The estimated values of the GM of Ryugu and a correction factor to our initial SRP model are 29.8 ± 0.3 m3/s2 and 1.13 ± 0.16, respectively.

Introduction
Hayabusa2 is an asteroid-sample return mission that is being conducted by Japan Aerospace Exploration Agency (JAXA). The spacecraft was launched in December 2014, performed an Earth swing-by utilizing Earth gravity in December 2015, and arrived at the target asteroid Ryugu in June 2018. Subsequent to its arrival at Ryugu, Hayabusa2 performed various observations and experiments, such as remote-sensing observations using onboard instruments, releases of a small rover and lander, ejection of the impactor, and sample collection from the surface and subsurface of Ryugu.
Some papers have been published on the results of the remote-sensing observations of Hayabusa2. Watanabe et al. (2019) discussed the formation process and evolution of the rotation of Ryugu based on the shape model and the standard gravitational parameter, i.e., the product of the gravitational constant (G) and mass of Ryugu (M). Kitazato et al. (2019) analyzed the spectrum absorption in the 3-μm-wavelength band obtained from the near-infrared spectrometer (NIRS3) observation and found that water was present in the form of hydrous minerals on the surface of Ryugu. Sugita et al. (2019) estimated the parent body of Ryugu on the basis of the spectral type of Ryugu that was determined from the data obtained by the optical navigation camera (ONC) and the data of thermal infrared imager (TIR) and laser altimeter (light detection and ranging, LIDAR). The evolution process from the parent body to Ryugu was also discussed based on the surface topography, spectrum, and thermal properties of Ryugu.
In these studies, the precise orbit of the spacecraft is indispensable to map the acquired remote-sensing data on the surface of Ryugu. In general, the spacecraft orbit is initially determined using radiometric observation data acquired at ground stations on the Earth. However, the precision of the orbit determination using radiometric data only is insufficient for mapping purpose (see “Orbit determination using LIDAR and AIT data sets” section) and should be improved with respect to the target body. Onboard instrument data—in case of Hayabusa2, the range data from the LIDAR and image data from the ONC—are useful for this purpose. Watanabe et al. (2019) performed a dynamic orbit determination and determined the GM of Ryugu using the LIDAR range, the automated image tracking (AIT) and the ground-control-point navigation (GCP-NAV) data besides of radiometric observation data, i.e., Doppler, range, and delta-differential one-way ranging (Delta-DOR) data. AIT data are a time series of the coordinates of the brightness centroid of the ONC images. GCP-NAV is an optical navigation technique used mainly during the special operations to determine the position and velocity of the spacecraft based on ONC-observed feature points on the asteroid surface (Terui et al. 2013).
Matsumoto et al. (2020) developed a simple method to improve the Hayabusa2 trajectory for the landing-site selection of the mission. They used LIDAR range data and a shape model of Ryugu that was developed using ONC images and determined the trajectory of Hayabusa2 using the Markov Chain Monte Carlo (MCMC) method such that temporal variations of the range observations geometrically fit the topographic fluctuations of Ryugu. They showed that the Hayabusa2 trajectory was greatly improved on using the LIDAR data. The advantage of this method is that the trajectory can be determined even outside the period of special operations if LIDAR data is available. LIDAR also performs range observations during the periods other than special operations, although the sampling frequency may vary (see “LIDAR range data” section). However, they first approximated the three-dimensional coordinates of the spacecraft using polynomials before the geometrical fitting to the topography. Owing to the use of such a non-dynamical approach, the velocities and other parameters, such as the GM of Ryugu, cannot be determined using this method.
In this study, we determine the orbit by dynamical approach, to improve the trajectory determined by Matsumoto et al. (2020) (MCMC orbit). In order to obtain a more precise orbit, in addition to the initial state vectors of the orbit, two parameters, i.e., the GM of Ryugu and a correction factor of the Hayabusa2 solar radiation-pressure (SRP) model, are also estimated. To estimate these parameters precisely, we use the data of multiple arcs with different altitudes, including the ones of the period when GCP-NAV data is unavailable. We use the AIT data as well as the LIDAR data. In principle, the AIT data are automatically calculated onboard at all times, although the data availability depends on whether the telemetry data are downlinked at that time. Our approach and software are independent of those used by Watanabe et al. (2019), and hence, our obtained GM value of Ryugu is useful for validating their results.
This paper is organized as follows. In “Data sets” section, we present the orbit arcs and details of the data sets used in this study. The method of orbit determination as well as software improvement is presented in “Orbit determination” section. In “Results and discussion” section, the results of the estimation of the Hayabusa2 orbit, GM of Ryugu, and correction factor of the Hayabusa2 SRP model are presented along with the corresponding discussion, and finally, the conclusion of this study is presented in “Conclusion” section.
Data sets
Hayabusa2 orbit and selection of arcs
The Hayabusa2 spacecraft is not orbiting Ryugu, but simply remaining around it, i.e., it is usually hovering at the home position (HP), which is 20 km above Ryugu and facing the sub-Earth direction (Tsuda et al. 2013). In the case of observations obtained at higher latitudes and low-altitude, or special events such as a gravity measurement, touch down, and ejection of a rover, lander, or impactor, Hayabusa2 starts from the HP, changes its position, and returns to the HP after the operation is completed.
In this study, we aim to determine not only the initial state vectors of the trajectory, but also the GM of Ryugu and a correction factor for the Hayabusa2 SRP model. The arcs used for the orbit determination are selected such that they are suitable for estimating these parameters. We use long, multiple, and different-altitude arcs in order to obtain a stable solution via the least-squares method (LSM). The use of multiple different-altitude arcs is advantageous for effectively separating the gravity and SRP forces (see “Estimation of the correction factor of the Hayabusa2 SRP model”section). Furthermore, it is preferable to include low-altitude arcs in the arc selection for a precise estimation of the GM of Ryugu. Table 1 presents the 14 arcs used for the orbit determination in this study.
LIDAR range data
The Hayabusa2 LIDAR is a pulse radar that comprises a YAG laser that produces a wavelength of 1064 nm (Mizuno et al. 2017). The pulse energy of each shot is 15 mJ, and the pulse width is 7 ns. LIDAR is used to measure the distance between the spacecraft and a target based on the measurement of the time duration between the transmission and reception of the laser pulse. The resolution of the time interval counter of the LIDAR is 3.33 ns, which corresponds to 0.5 m of the one-way distance. The LIDAR has two telescopes for detection of laser light (Far and Near) to meet the dynamic range requirement of the Hayabusa2 (30 m to 25 km). Under the Automatic Gain Control (AGC) operation mode, the optical-range mode is automatically switched from Far to Near when the distance between the spacecraft and the target is less than 1 km. The fields of view of the Far and Near optical telescope modes are 1.5 mrad and 20.4 mrad, respectively.
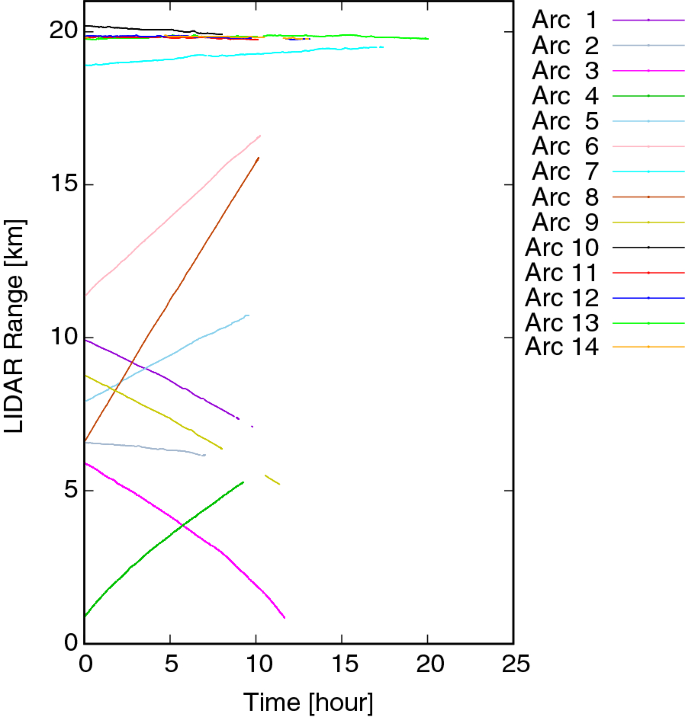
In this study, we use the LIDAR time-series range data provided by the Hayabusa2 LIDAR team. The data contains the LIDAR-measured range and related telemetry data derived from the Hayabusa2 science data packets called “AOCSM”. The time resolutions of the range data are 1 Hz for scientific mapping and special operation periods, e.g., gravity measurement operations, and 1/32 Hz for other periods. Figure 1 shows the temporal changes of the LIDAR-range observations used in this study.
Temporal change of LIDAR-observed altitude for each arc. Arc numbers are listed in Table 1
Image tracking data
The Hayabusa2 ONC system consists of three charge-coupled-device (CCD) cameras—telescopic nadir view (ONC-T), wide-angle nadir view (ONC-W1), and wide-angle slant view (ONC-W2)—of focal length 120.50 mm, 10.22 mm, and 10.34 mm, respectively (Kameda et al. 2017; Suzuki et al. 2018; Tatsumi et al. 2019). In this study, we use AIT data generated on board from an ONC-W1 image. The AIT data contains the time series of XONC (XONC, YONC) and AONC. As Hayabusa2 is facing the sub-Earth direction, except for the conjunction period, when Ryugu is on the other side of the Sun to the Earth, the daylight hemisphere of Ryugu can always be observed by the spacecraft. XONC is a two-dimensional center coordinate of the brightness of the ONC-W1 image, i.e., centroid coordinates. The illumination condition of the pixels on each image depends not only on the shape of Ryugu’s limb, but the shadow produced by the surface topography. AONC is the number of the bright pixels used for the centroid-coordinate calculation and can be converted to the approximate distance between the center of Ryugu and Hayabusa2 (see “Software” section) when the whole image of Ryugu is captured by ONC-W1. ONC-W1 has a 1024 × 1024 detector array with a pixel size of 0.013 mm, and the field of view (FOV) is 69.71° × 69.71°. That is, 1 pixel corresponds to 0.06808° (1.1882 mrad). On the other hand, 0 ≦ XONC ≦ 512, 0 ≦ YONC ≦ 512, and 0 ≦ AONC ≦ 512 × 512, because the 1024 × 1024 image array is binned to 512 × 512 in the onboard data processing. Thus, 1 pixel of the AIT data corresponds to 0.13616° (2.3764 mrad). The time resolution of the data is between 1/2048 Hz and 1/16 Hz for the arcs used in this study (Table 1). Figure 2 shows the time series of XONC for each arc.
Temporal change in image-tracking-data coordinate for the duration of each arc. Arc numbers are listed in Table 1
Ancillary data
The precise boresight coordinate of the LIDAR instrument with respect to the center of the Hayabusa2 spacecraft was determined by Noda et al. (2019), and we use it in this study. As for the coordinate of the ONC-W1 instrument with respect to the center of the spacecraft, we use that in the Hayabusa2 Science Data Archives (JAXA 2019). The attitude of the Hayabusa2 spacecraft is also obtained from the archives, and the precision is better than 0.03°. The temporal mass-change data of the Hayabusa2 spacecraft are provided by JAXA.
Orbit determination
Software
We use the orbit determination software c5 ++ (Otsubo et al. 2016; Hattori and Otsubo 2019) that was originally developed for the data analysis of satellite laser ranging (SLR) between ground stations on the Earth and SLR satellites. This study presents the first case of the software being applied to an interplanetary spacecraft. Various features of the software are reorganized or newly developed for the orbit determination in this study as follows.
Improvement to use SPICE kernel format data in c5 ++
SPICE is a framework used for handling ancillary space-science data and has been developed by the Navigation Ancillary Information Facility of the Jet Propulsion Laboratory (Acton 1996; Acton et al. 2018). In the Hayabusa2 project, the auxiliary data of the spacecraft, such as attitude and clock, are released in the SPICE kernel format as well as the physical parameters and ephemeris of Ryugu and other bodies. We are required to implement the transformations of various reference frames and, therefore, extend c5 ++ such that it can use the data of the SPICE kernel format.
Development of a function for analyzing LIDAR data
LIDAR range data (ρLIDAR) is the observed value of the distance between the Hayabusa2 spacecraft and the surface of Ryugu. For the orbit determination, it is necessary to compute the corresponding range value in the software. The range ρc is given by the following equation:
where x (x, y, z) is a position vector of the Hayabusa2 spacecraft at laser emission time. x0 (x0, y0, z0) is a position vector of the footprint of the LIDAR laser beam on the surface of Ryugu. x0 is determined by applying corrections of change of the Ryugu position as seen by the spacecraft and rotation of Ryugu during the travel time of the light. The origin of these vectors is set to the center of Ryugu.
In principle, a footprint position can be calculated as the interception of a LIDAR laser beam and the surface of Ryugu. However, especially at the initial stage of the orbit determination, the footprint calculated using such a method may depart from the actual footprint because there exists a large uncertainty in the spacecraft position. In order to derive a more realistic footprint position, in c5++, the method applied by Matsumoto et al. (2020) is integrated into the footprint estimation procedure. The footprint is re-estimated using the improved orbit obtained at each iteration step, and we obtain the final solution after two to three iterations.
Development of a function for analyzing the centroid coordinate in the AIT data
A centroid coordinate XONC (XONC, YONC) (refer to “Image tracking data” section) and the focal length of the ONC-W1 camera rf are represented using a spacecraft-fixed centroid direction vector at the focal point xONCs (xONCs, yONCs, zONCs), as presented in the following equations:
where Xpix (Xpix, Ypix) is the pixel size of the ONC-W1 camera, and Xshift (Xshift, Yshift) is a shift value of the defined origin of the ONC-W1 coordinate from the center of the image. In Eq. (2), the known parameters are Xpix, Xshift and rf. For Xpix and rf, we use in-flight calibrated values obtained by Suzuki et al. (2018) and Tatsumi et al. (2019). The value of Xshift is (−256, −256) since the pixel values of XONC start from the upper left corner of the 512 × 512-pixel array, not from the center.
We derive xONCs from each XONC observation using Eq. (2) and then convert it into a centroid direction vector in the spacecraft-centered inertial frame xONCi by multiplying a coordinate transformation matrix. Finally, right ascension αONC and declination δONC of the centroid direction in the spacecraft-centered inertial frame, which are the observation values input into c5++, are derived from xONCi using the following equations:
The corresponding computed right ascension αc and declination δc of the centroid direction in the spacecraft-centered inertial frame are derived as follows. We define Xv (Xv, Yv) as a coordinate of a projection of each vertex of the Ryugu shape model onto the image plane as obtained from ONC-W1. Furthermore, the following two inner products are introduced: β is an inner product of a vector from the center of Ryugu to a vertex and a vector from the spacecraft to the vertex, and γ is an inner product of a vector from the center of Ryugu to a vertex and a vector from the Sun to the vertex. For a vertex to be photographed by ONC-W1, the following three conditions should be satisfied: (1) the projected vertex coordinate should be in the field of view of ONC-W1, i.e., 0 ≦ Xv ≦ 512, and 0 ≦ Yv ≦ 512; (2) the vertex should be visible from ONC-W1, i.e., β ≦ 0; and (3) the vertex should be illuminated by the Sun, i.e., γ ≦ 0. We check these conditions for all the vertices of the shape model of Ryugu at each time of obtaining the AIT observations and obtain the projected image coordinates Xv of the vertexes that could be photographed by ONC-W1.
In a real ONC-W1 image, the distortion in the peripheral areas of the field of view was non-negligible. Suzuki et al. (2018) presented an equation for converting a distorted image into a non-distorted image. In our study, the inverse transformation equation, i.e., the equation that provides a distorted image from a non-distorted image, is required. We prepare the inverse transformation equation in the same manner as that of the transformation equation presented by Suzuki et al. (2018). The coefficients in the equation are estimated via the LSM and using distorted and non-distorted test data bases on the study of Suzuki et al. (2018). The maximum error of the conversion is 0.5 pixels. Using the inverse transformation equation, we reproduce a distorted ONC-W1 image coordinate Xv′ from the non-distorted one Xv. Finally, all Xv′ are stored in 512 × 512 pixel bins to obtain data of the same resolution as that of the observed AIT. The computed centroid coordinate Xc is derived as follows:
where Xij is the center coordinate of each bin of the pixel. aij is an index that indicates whether the pixel is illuminated; aij = 1 if the pixel is illuminated, and aij = 0 otherwise. For each bin, the average value of γ of all of the contained vertexes is calculated. If this average value is −0.5 or less, we assume that the pixel is illuminated and set aij as 1; otherwise aij is set as 0. Before Xc is fed into c5++, it is converted to computed right ascension αc and declination δc as the same way of observed values.
Development of a function for analyzing the number of pixels in the AIT data
AONC in “Image tracking data” section reflects the size of Ryugu as observed from ONC-W1 and can be used to approximate the distance between the center of Ryugu and Hayabusa2 (dONC), although it is only valid when the whole of Ryugu is captured within the field of view of ONC-W1; all the arcs used in this study satisfied this condition.
We obtain dONC from AONC using the following equation:
where C and n are constants, the values of which depend on the conditions of illumination and rotation of Ryugu at the observed time. For example, in the case of arc No. 3 in Table 1, C = 339043 [m pixeln], and n = 0.59. C and n are derived by fitting a power function to the model of the dONC—AONC plot, which is derived from a calculation that comprises the use of a shape model of Ryugu. Furthermore, the computed distance dc between the center of Ryugu and Hayabusa2 is calculated based on the spacecraft position and Ryugu’s ephemeris in c5++.
Force models
The motion of Hayabusa2 that is disturbed by various perturbing forces is described in the Ryugu-centered reference frame in this study. Figure 3 shows the magnitude of the accelerations caused by several significant forces. The altitudes of the arcs used in this study range from 0.849 to 20.2 km (Table 1). At the altitude of the HP (20 km), the SRP force causes the most significant acceleration. The accelerations caused by the GM force of Ryugu gradually increase as the altitude decreases and become the dominant acceleration at altitudes less than 16.5 km. The effects of the GM and SRP forces are particularly significant as perturbing forces for the arcs we used, and precise modeling of these forces is essential for improving the precision of orbit determination. Thus, we estimate the GM of Ryugu and a correction factor for the Hayabusa2 SRP model.
The GM of Ryugu is initially set as 30.0 m3/s2 based on the study conducted by Watanabe et al. (2019). This value is estimated and updated in the orbit-determination process. For the calculation of the SRP force, the spacecraft mass is required because the magnitude of the SRP force is inversely proportional to the spacecraft mass. The spacecraft mass is constantly losing mass while it is in orbit. During the 8-month period considered in this study (Table 1), Hayabusa2 executed various events, and its mass decreased owing to its fuel consumption and the release of payloads. Therefore, we use the realistic spacecraft-mass-change data, as mentioned in “Ancillary data” section for obtaining an accurate estimation of the SRP force. In the case of this study, mass decrease due to fuel consumption within each arc is slight. However, after some events, most notably, the operations of Minerva-II1 rover and MASCOT lander releases performed on September 20–21 and October 2–4 2018, respectively, the spacecraft significantly loses the mass.
Models of the spacecraft shape and surface reflectivity are also required for the SRP-force calculation. As an initial Hayabusa2 shape model, we use a model comprising two solar panels and one cube spacecraft of dimensions 4.23 × 1.36 m2 and 1.00 × 1.60 × 1.25 m3, respectively. The initial specular and diffuse reflectivity are set as 0.01 and 0.08 for the solar panels (Ono et al. 2016) and 0.375 and 0.255 for the cube spacecraft (typical values for general spacecraft), respectively. The SRP force is initially calculated using the aforementioned simple spacecraft shape and reflectivity models, the mass-change data and the incidence angle on each panel of the spacecraft shape model, which is obtained from the position of the Sun with respect to the spacecraft and the attitude data, and updated by estimating a correction coefficient in the orbit determination.
As shown in Fig. 3, the accelerations due to other perturbing forces are not as significant as the ones due to the GM of Ryugu and the SRP forces. In the Ryugu-centered reference frame, the acceleration from the Sun represents the most significant third-body perturbation. At the HP it is approximately two orders of magnitude smaller than the acceleration resulting from SRP and decreases as the altitude decreases. Accelerations caused by the C20 and C40 terms of Ryugu’s gravity field, which are the second- and third-largest gravity-field terms after GM, increase as the altitude decreases, although they are one-to-three orders of magnitude smaller than the GM acceleration even below an altitude of 1 km. We consider these forces as perturbing forces in the orbit integration, but did not estimate the related parameters. The three-body forces from the Sun and other solar system planets and higher terms of the gravity field of Ryugu up to degree and order 10 are considered in the orbit integration. The Sun, planetary, and Ryugu ephemerides used for the calculation of the three-body forces are presented in “Shape model and rotation parameters of Ryugu, and ephemerides of Sun, planets, and Ryugu” section. The model of the higher degree and order of the Ryugu gravity field are obtained from the spherical harmonic expansion of the shape model based on the assumption of the globally constant density of 1.19 g/cm3 (Watanabe et al. 2019) and shown in Additional file 1: Table S1.
Shape model and rotation parameters of Ryugu, and ephemerides of Sun, planets, and Ryugu
We use Ryugu’s shape model of the version SHAPE_SPC_3M_v20181109, an updated version of the model SHAPE_SPC_3M_v20180829 developed by Watanabe et al. (2019). This model comprises 3,145,728 facets and 1,579,014 vertexes. The model was developed with the stereo-photo-clinometric (SPC) technique using hundreds of images. To estimate the error magnitudes of the SPC model, Watanabe et al. (2019) compared the topographic cross sections derived from the shape model and LIDAR measurements at some of the selected boulders and reported that the observed differences were less than 2 m.
The orientation parameters of Ryugu, which is required for the coordinate transformation between Ryugu-fixed and inertial frames, were also determined as by-products of the shape model production, and we used them. The ecliptic longitude and latitude of the pole direction are 179.3° and −87.44°, respectively, and the rotation period is 7.63262 ± 0.00002 h. The Sun and planet positions and velocities are derived from DE430 ephemerides provided by JPL (Folkner et al. 2014), and the ones of Ryugu are obtained from the Ryugu ephemeris provided by JAXA (see “Shape model and rotation parameters of Ryugu, and ephemerides of Sun, planets, and Ryugu” section.
Orbit determination
We estimate the initial state vector of each arc, which is an arc-specific parameter, the GM of Ryugu and the coefficient of the Hayabusa2 SRP model, which are global parameters and common to all the arcs. In the real situation, it is empirically known that an SRP coefficient temporally changes the value by other unmodelled factors, as will be discussed in “Estimation of the correction factor of the Hayabusa2 SRP model” section. However, we do not incorporate these multiple factors into the SRP model as additional model parameters because the estimation becomes more unstable. As another approach, it is also possible to estimate the SRP coefficient of each arc as an arc-specific parameter. However, in that case, separation of the effects of GM and SRP forces by using different altitude arcs could be achieved insufficiently, and the uncertainties of the estimated parameters could become larger. Therefore, in this study, the SRP coefficient is estimated as one of the global parameters. We first perform orbit determination for each arc with global parameters fixed and obtain the improved arc-specific parameters. Subsequently, using the improved arc-specific parameters as the initial parameter values, orbit determination is performed again to estimate the global parameters (and further improved arc-specific parameters). Such a two-step approach is practical for realizing the fast convergence of the solution, in the case that the error of the initial arc-specific parameters is much greater than that of the initial global parameters.
Figure 4 shows the overview of the orbit determination in this study.
In c5++, (1) the orbit of each arc is first generated using force models. As the starting value of the initial state vector of each arc, we use that of the MCMC orbit in the solution of Matsumoto et al. (2020). The initial value of the GM of Ryugu is set as 30.0 m3/s2, as mentioned in “Force models” section. The SRP coefficient is initially set as 1.0. The computed observables (LIDAR range, centroid direction, and/or distance between the center of Ryugu and the spacecraft) for each observed time are then obtained from the generated orbit. In order to derive the computed LIDAR range value in this orbit determination process, the coordinates of the LIDAR footprint are required in addition to the spacecraft position, as shown in Eq. (1). In principle, the footprint can be estimated from the spacecraft position and attitude information. However, in this method, especially at the initial stage of iterations, such a footprint estimation provides an inaccurate value because of the significantly inaccurate orbit. As a more reasonable footprint coordinate, we use the LIDAR footprint coordinates generated using the MCMC method in the process of trajectory estimation presented by Matsumoto et al. (2020). The footprint coordinates are obtained in the process of estimating the MCMC orbit such that the topography obtained from the shape model and the LIDAR observation data are geometrically consistent.
Then, (2) the unknown parameters are estimated using the LSM, in order to minimize the difference between the observed and computed observables. In the LSM, the LIDAR footprints are fixed and not estimated. We introduce the weight w of ρLIDAR, XONC, or AONC for the LSM as follows:
where ε is the error in the observation. The errors of ρLIDAR and XONC were assumed to be 1.5 m and 0.1°, respectively. The error in AONC is given as an apparent angle of view of the Ryugu body as observed from Hayabusa2, which is assumed to be 2.0°. It is converted in c5++ into the error in the distance to make it consistent with dONC.
(3) The estimated values of the initial state vectors, the GM of Ryugu, and the SRP coefficient derived based on the LSM are improved by some iterations (the shaded part in Fig. 4).
(4) The updated orbit is generated from these estimated parameters.
(5) Using the updated orbit as a new initial input orbit, the LIDAR footprint coordinates and spacecraft positions are re-estimated using the MCMC method and used for the LIDAR range calculation in the next iteration step. The iterations outside the shaded part in Fig. 4 are repeated 2–3 times to obtain the final estimated values of the initial state vectors, the GM of Ryugu and the SRP coefficient.
Results and discussion
Orbit determination using LIDAR and AIT data sets
As mentioned in “Introduction” section the Hayabusa2 orbit can be determined by radiometric observation from the Earth. In general, the precision of radiometric sciences is about 0.03 mm/s for 60 s integration time, 1–2 m and 2.5 nrad for Doppler, range and DDOR observations, respectively (Turyshev 2011). 2.5 nrad corresponds to about 600 to 750 m at the surface of Ryugu, as Hayabusa2 is about 250 to 300 million km away from the earth during the rendezvous phase with Ryugu. Considering that the mean diameter of Ryugu is about 900 m, it is difficult to obtain local positions on the surface of Ryugu by only using this orbital information. Thus, orbit determination with respect to Ryugu is desired.
We first perform orbit determination using the LIDAR range data only. In the case of an orbiter of a body, an initial state vector (three-dimensional initial position and velocity vectors) of the spacecraft can be determined from the range data by using LSM, if the number of range observations is sufficiently large. However, as mentioned in “Hayabusa2 orbit and selection of arcs” section , Hayabusa2 does not orbit Ryugu, but hovered above it. This means that Hayabusa2 does not move actively with respect to Ryugu, and thus, a separation of the three direction components (line-of-sight direction of the range observation and the other two orthogonal directions) is insufficient for stable orbit determination. In particular, the correlation between the two directions orthogonal to the ranging direction is significantly high. Thus, a three-dimensional solution cannot be obtained. If strong constraints are provided for the other two directions, we can obtain the radial components of the state vector, which correspond to the direction of LIDAR range observation. However, in this case, the other two components are hardly improved because of the strong constraints.
Next, orbit determination is performed using only AIT data. As stated in “Image tracking data” section, the AIT data include AONC and XONC, which can be converted into the distance between the center of Ryugu and Hayabusa2, and the right ascension and declination angles of the centroid direction in the spacecraft-centered inertial frame, respectively. By using these observation values corresponding to the radial directions and the other two directions orthogonal to it, it is possible to obtain all of the six components of the initial state vector stably. Figure 5a shows the error ellipsoid derived from the solution covariance matrix. The case of the orbit determination of arc No. 3 is presented as an example. The root-mean-squares of the residual of the observed minus computed ((O − C) RMS) values of the distance between the center of Ryugu and Hayabusa2 and the centroid direction are 29.4 m and 0.0333°, respectively. As shown in Fig. 5a, in this approach, the error of the obtained solution is significantly greater in the ranging direction than that in the other two directions orthogonal to it. The AIT data are based on the two-dimensional camera image data, which has less sensitivity in the radial direction. Furthermore, the observed value of AONC is provided as an integer value. As a result, the resolution of dONC is insufficient for representing a small change in the distance.
Error ellipsoids derived from solution covariance matrices. a The cases of orbit determinations of arc No. 3 in Table 1 using centroid direction and number of bright pixels of AIT data (blue) and using both centroid direction of AIT data and LIDAR range data (red). Green arrow indicates the direction of the center of Ryugu. b Enlarged view of a
To compensate for defects in the two approaches above, we finally perform orbit determination using the LIDAR data and XONC of the AIT data. The solution can be solved stably because the observed data corresponding to the three directions are available. Furthermore, by replacing AONC of the AIT data with the LIDAR range data, the accuracy in the radial direction is significantly improved, as shown in Fig. 5a and b. The (O − C) RMSs of the range and centroid direction are 2.34 m and 0.0329°, respectively, for arc No. 3.
Estimation of LIDAR footprint using MCMC method
In the case of the range observation from ground stations, such as SLR, the ground station coordinates can be estimated as one of the global parameters in orbit determination by using LSM. Such an estimation is only possible when there are multiple range observations for each ground station. In contrast, in the case of the Hayabusa2 LIDAR, in principle, the footprint coordinates can be derived if the spacecraft position and attitude are known for each observation time. However, in actuality, it is impossible to obtain precise footprint coordinates using such a method if inaccurate spacecraft orbit data is used. Furthermore, in contrast to SLR, there is only one range observation corresponding to each footprint, and thus, the LSM approach cannot be used for the footprint coordinate estimation. Therefore, as shown in Fig. 4, we do not estimate footprint coordinates as one of the estimated parameters of the LSM, but leave it to MCMC method outside the LSM. This approach is useful for realizing quick convergence of the solution as compared to that in the case of the direct footprint calculation from the updated orbit and attitude data. The updated orbit determined using the LSM is based on the footprints obtained by MCMC method in the initial/previous iteration step. If there exists a significant error in the footprints, the updated orbit is not always closer to the correct solution than that before the update. As a result, the direct footprint calculation from the updated orbit and attitude data requires a number of iterations to provide the final converged solution, and it sometimes diverges during the iteration. In contrast, only a few iterations are required to obtain converged footprints in the case of the footprint estimation using the MCMC method. The iteration is stopped when the differences between footprints estimated using the MCMC method and those calculated using the orbit and attitude data are small. Figure 6a shows the residuals of the observed LIDAR range of arc No. 3 and the corresponding computed range obtained from the finally determined footprint and the spacecraft orbit, after removing the long-wavelength variation by fitting quartic equations. On removing the long wavelength components, the small variations become more significant. The small variations correspond inversely to the surface fluctuation of the topography. Figure 6b shows the difference between the observed and computed ranges and Fig. 6c shows the difference between the observed and computed centroid directions, respectively.
a Residuals of LIDAR range of arc No. 3 in Table 1 (blue) and the corresponding computed range (red) after removing long-wavelength components via quadratic equation fitting. b The difference between the observed and computed ranges for arc No. 3. c The difference between observed and computed right ascension (blue) and declination (red) angles of the centroid directions viewed from the Hayabusa2 spacecraft for arc No. 3
Estimation of the correction factor of the Hayabusa2 SRP model
In some cases of Earth-orbiting geodetic satellites, the surface area and surface reflection characteristics of the spacecraft are examined before the launch for precise modeling of the SRP force for highly precise applications. However, generally such a model is not constructed. In the case of Hayabusa2, a generalized sail dynamics model was developed by Ono et al. (2016) in order to model the transitional and rotational motion of the spacecraft induced by the SRP force. In this study, we consider a simple SRP model, as shown in “Force models” section, and estimate the correction factor as one of the global parameters of the orbit determination. This factor is a constant that corrects the errors of the surface area and surface reflection characteristics of the spacecraft.
As shown in Fig. 3, the magnitude of the accelerations on the spacecraft due to the SRP force and GM force of Ryugu exhibit different behaviors for the altitude change. The magnitude of the acceleration due to the GM force of Ryugu is inversely proportional to the square of the distance from Ryugu. In contrast, magnitude of the acceleration due to the SRP force does not depend on the distance from Ryugu. It depends on the solar incident angle to the spacecraft surface and the mass of the spacecraft. In this study, we use multiple arc data comprising different altitudes, as shown in Table 1. It is helpful to separate the effects of the two forces in the orbit determination and derive more plausible values of the two parameters, i.e., the GM of Ryugu and the correction factor of the Hayabusa2 SRP model. The obtained value of the correction factor is 1.13. In actuality, it is empirically known that an SRP coefficient is not constant and temporally varies due to various environmental factors (e.g., Hattori and Otsubo 2019). In the case of Hayabusa2, for example, the effect of variation of the temperature distribution of the spacecraft depending on which onboard instruments the internal heater is assigned to for each phase, the effect of holes in the structure of the spacecraft, which are made after the release of payloads, and the effect of the secular degradation of the surface material are considered as some of the factors. Therefore, the SRP coefficient derived in this study is an average value for the 14 arcs. In the real situation, the SRP coefficient is not a fixed value, but temporally variable. We estimate the SRP coefficient for each of the 14 arcs by fixing the GM of Ryugu to the value shown in “Estimation of the GM value of Ryugu” section. The results (Table 2) show that the range of the variation is ± 0.16.
Estimation of the GM value of Ryugu
Watanabe et al. (2019) estimated the GM in their orbit determination. The estimated GM value is 30.0 ± 0.4 m3/s2. As mentioned in “Introduction” section, the time-series data of ONC image landmark coordinates (i.e., GCP-NAV) is involved in this determination. It is useful to fix the relative position of Hayabusa2 at each time with respect to the feature points on the surface of Ryugu. The GCP-NAV has the advantages of high spatial resolution (1024 × 1024) and small uncertainties in the intercept coordinates of the line-of-sight direction of ONC and Ryugu’s surface. Thus, a precise orbit determination is expected, especially in the two directions orthogonal to the ranging directions. However, the availability of GCP-NAV data is limited mainly to the arcs for special operations. In this study, we use multiple arcs with different altitudes for obtaining a precise estimation of the correction factor of the SRP model. The majority of these arcs used in this study are not the arcs of a special operation period when GCP-NAV data are available. We only use the AIT and LIDAR data and do not use the GCP-NAV data. We estimate the coordinate of the LIDAR footprint on the surface of Ryugu at each observation time by the MCMC method. As stated in “Estimation of LIDAR footprint using MCMC method” section, although several iterations are required to obtain a plausible footprint coordinate by the method, our approach is useful to fix the relative position of Hayabusa2 with respect to a footprint point on the surface of Ryugu at each time. Thus, our approach enables precise orbit determination even for the arcs where GCP-NAV is unavailable.
The estimated GM value of Ryugu in our study is 29.8 ± 0.3 m3/s2, which is consistent with the one presented by Watanabe et al. (2019). The uncertainty of the estimated value is caused by the uncertainty of the SRP coefficient (see “Estimation of the correction factor of the Hayabusa2 SRP model” section). The density calculated using the GM and the volume of the used shape model (0.379 km3) is 1.18 g/cm3. We also estimate the GM using only the descending (arc No. 3) or ascending arc (arc No. 4) of the gravity measurement operation by fixing the SRP coefficient to 1.13. These two arcs contribute most to the determination of the GM because of the low altitude. The results are 29.79 m3/s2 and 29.84 m3/s2 for the descending and ascending arcs, respectively.
Comparison of the determined orbit with MCMC orbit
The initial state vector of each arc is finally estimated using the correction factor of the SRP model and the GM of Ryugu determined in “Estimation of the correction factor of the Hayabusa2 SRP model” section and “Estimation of the GM value of Ryugu” section . Table 3 shows the (O − C) RMSs of the range and centroid direction, respectively. The (O − C) RMSs derived from the corresponding MCMC orbits are also presented for the purpose of comparison. The averaged (O − C) RMSs of range and centroid direction for the 14 arcs are 1.95 m and 0.143° for the MCMC orbits, while 1.44 m and 0.0231° for the orbits determined in this study, respectively.
The uncertainty of attitude data limits the precision of orbit determination. As stated in “Ancillary data” section, the nominal precision of attitude data is better than 0.03°. The effect of attitude uncertainty on the MCMC orbit determination is relatively small because the footprint size of LIDAR is 0.086°, which is larger than attitude uncertainty. On the other hand, as shown in Additional file 2: Table S2, the XONC is given in units of pixels with better precision than four decimal places. Since 1 pixel of the XONC data corresponds to 0.13616° (see “Image tracking data” section), the precision corresponds to better than 1.3616 × 10−5°, which is much smaller than the uncertainty of attitude data. Thus, in the orbit determination in this study, the uncertainty of the attitude is one of the factors which limits the orbit precision of the direction perpendicular to LIDAR-beam direction. From another point of view, in principle, there is a way to adjust pointing from the image data, since the precision of the data is better than the attitude knowledge. This could also help improve attitude knowledge of the spacecraft.
The error in the shape model is also a factor to limit the precision of orbit determination. The shape model in this study consists of about 3 million facets and the surface area of each of the facets is less than 1 m2 on average. Topographic features smaller than each facet are not represented in the model. However, this effect on the orbit determination in the LIDAR-beam direction is small because the surface LIDAR footprint size is about 30 m in diameter when the spacecraft altitude is 20 km, which is larger than the mean facet area of the model. The finite number of facets and vertexes of the shape model also affects the calculation of the computed centroid coordinates (see “Software” section, which is calculated based on the projection of the shape model on the image plane, although the magnitude of the error cannot be estimated.
There are two essential differences between the orbit determination in this study and that performed by Matsumoto et al. (2020). The first is that our orbit is not determined geometrically but dynamically. Therefore, we can estimate all the six components of the initial state vector (three-dimensional position and velocity components) for each arc, and also GM of Ryugu and the correction factor of the SRP model, while only the position coordinates for each LIDAR observation time can be estimated using the method of Matsumoto et al. (2020).
The second difference between our method and that of Matsumoto et al. (2020) is that we used AIT data for the orbit determination in addition to the LIDAR data. As shown in Table 3, the (O − C) RMS of the centroid direction obtained in our study is improved by approximately one order of magnitude as compared to that of the MCMC orbit. This means that the orbit is largely improved in the two directions orthogonal to the ranging direction. As a result, the footprint coordinates of the range observation obtained using the two methods exhibit a difference. The magnitude of this discrepancy depends on the arc (Fig. 7). Despite the large change in the footprint coordinates, the (O − C) RMSs of the range are of almost the same order of magnitude in the two methods, and in the case of some arcs, our result was worse than that of the MCMC orbit. The results show that there are multiple similar topographic profiles that fit well geometrically with the LIDAR-range variation of each arc and it is difficult to determine a unique trajectory if only LIDAR data is used. Figure 8 shows the topographic profiles of the Ryugu shape model along with the LIDAR footprints derived from our estimated orbit and the MCMC orbit. For example, the figure of arc No. 1 shows that the two profiles are very similar, although the geographical latitude and longitude of the footprints are different from each other, as shown in Fig. 7. The introduction of the AIT data helped to decrease the uncertainty of geometric LIDAR data fitting by providing the observations of the two directions orthogonal to the ranging directions. However, it should be noted that, even in our estimation, the MCMC method of Matsumoto et al. (2020) is used to estimate and improve the footprint coordinates in each iteration step, as stated in “Estimation of LIDAR footprint using MCMC method” section. This is useful for realizing a quick convergence of the solution for the orbit determination.
Comparison of computed LIDAR footprint coordinates derived using the MCMC method presented by Matsumoto et al. (2020) (red) and this study (blue). The hourly footprint position is indicated by a dot representing the longitudinal position differences. The background shows the topographic height of the Ryugu shape model measured from the center of Ryugu
Topographic profiles of the Ryugu shape model along with the LIDAR footprints of the MCMC orbit presented by Matsumoto et al. (2020) (red) and our determined orbit (blue)
In the study of Matsumoto et al. (2020) and this study, the same attitude data are used. Therefore, the footprint discrepancies between the two methods shown in Fig. 7 directly correspond to the latitudinal and longitudinal differences of the orbits. The error in the latitudinal direction of the orbit has a greater effect on the estimation of Ryugu’s GM than that of the longitudinal direction. The 0-order term of the gravity force is expressed as GM/r2, where r is the distance between Ryugu’s center and the spacecraft. As the shape of Ryugu is not a sphere but a spin-top shape, the displacement of the orbit in the latitudinal direction is directly linked to the difference in r, which results in a change in the value of the gravity force. Therefore, the introduction of the AIT data is also important from the viewpoint of GM estimation.
Conclusion
The MCMC orbits determined by Matsumoto et al. (2020) are improved to dynamically estimated precise ones by using the AIT data as well as LIDAR range data. By dynamic orbit determination, we are able to solve all six components of the initial state vector of each arc. The (O − C) RMSs of the LIDAR range and the centroid direction are 1.36 m and 0.0270° on average for all the arcs. By using the AIT data, we can correct the misfit of LIDAR range data to geometrically similar topography caused in the MCMC orbit determination. Thus, the AIT data contributes significantly to the improvement of the MCMC-orbit error by providing information regarding the directions orthogonal to the ranging direction. By dynamic approach, we can also estimate the GM of Ryugu and a correction factor of the Hayabusa2 SRP model in order to obtain a more precise orbit. The estimated value of the correction factor of the SRP model is 1.13 ± 0.16 with respect to our initial SRP model. The GM of Ryugu obtained in this study is 29.8 ± 0.3 m3/s2. This value is consistent with the results of Watanabe et al. (2019) estimated using a different method and software. We do not use GCP-NAV data, which is available for limited number of arcs. For example, when Hayabusa2 is hovering at the HP during several arcs at altitudes of about 20 km shown in Table 1 (arc No. 7, 10, 11, 12, 13 and 14), GCP-NAV navigation is not performed. Our orbit-determination method is applicable not only to special operation arcs, but also to such non-special arcs.
Our approach provides added values, for example, to the orbit determination of the following cases:
(1) A case that it is difficult to separate each of three direction components of the orbit. More concretely, a case when the spacecraft does not actively move with respect to the target body, such as rendezvous.
(2) A case that orbit determination is required to use many arc data including not only special operation arcs, but also non-special arcs. For example, a case of estimating long-period variable components of the orientation parameters of the target body.
(3) A case that it is required to map remote-sensing data even outside of the special operation periods.
Thus, our method will be useful not only for Hayabusa2 mission, but also for future small body missions as one of the methods to obtain a precise orbit.
Availability of data and materials
The use of Hayabusa2 LIDAR time-series range data, and the use of SPICE kernels including precise boresight coordinate of LIDAR instrument, the coordinate of ONC-W1 instrument with respect to the spacecraft, attitudes of the spacecraft, the orientation parameters of Ryugu, ephemeris of Ryugu and the shape model of Ryugu will be released in public by the end of 2020 and will be available from the following URL.
LIDAR time-series range data:
http://darts.isas.jaxa.jp/pub/hayabusa2/lidar_bundle/browse/
SPICE kernels:
http://darts.isas.jaxa.jp/pub/hayabusa2/spice_bundle/document/spiceds_v001.html
The AIT data are provided as a supplementary online material of this manuscript (Additional file 2: Table S2).
The temporal mass-change data of the spacecraft is not open in public because it is part of confidential information related to the technical condition of the spacecraft. The use is strictly restricted to the mission members only.
Abbreviations
- AGC:
-
Automatic Gain Control
- AIT:
-
Automated image tracking
- CCD:
-
Charge-coupled-device
- Delta-DOR:
-
Delta-differential one-way ranging
- GCP-NAV:
-
Ground-control-point navigation
- HP:
-
Home position
- LIDAR:
-
Light detection and ranging laser altimeter
- LSM:
-
Least-squares method
- MCMC:
-
Markov Chain Monte Carlo
- NIRS3:
-
Near-infrared spectrometer
- (O − C) RMS:
-
Root mean squares of the difference between the observed and computed values
- ONC:
-
Optical navigation camera
- ONC-T:
-
Optical navigation camera for telescopic nadir view
- ONC-W1:
-
Optical navigation camera for wide-angle nadir view
- ONC-W2:
-
Optical navigation camera for wide-angle slant view
- RMS:
-
Root mean squares
- SRP:
-
Solar radiation pressure
- SLR:
-
Satellite laser ranging
- SPC:
-
Stereo photo clinometry
- TIR:
-
Thermal infrared imager
- YAG:
-
Yttrium aluminum garnet
References
Acton CH (1996) Ancillary data services of NASA’s navigation and Ancillary Information Facility. Planet Space Sci 44:65–70. https://doi.org/10.1016/0032-0633(95)00107-7
Acton C, Bachman N, Semenov B, Wright E (2018) A look towards the future in the handling of space science mission geometry. Planet Space Sci 150:9–12. https://doi.org/10.1016/j.pss.2017.02.013
Folkner WM, Williams JG, Boggs DH et al (2014) The planetary and lunar ephemerides DE430 and DE431. Interplanet Netw Prog Rep 196:42–196
Hattori A, Otsubo T (2019) Time-varying solar radiation pressure on Ajisai in comparison with LAGEOS satellites. Adv Sp Res 63:63–72. https://doi.org/10.1016/j.asr.2018.08.010
JAXA (2019) Hayabusa2 Science Data Archives. https://www.darts.isas.jaxa.jp/planet/project/hayabusa2/. Accessed 20 Jan 2020
Kameda S, Suzuki H, Takamatsu T et al (2017) Preflight calibration test results for optical navigation camera telescope (ONC-T) onboard the Hayabusa2 Spacecraft. Space Sci Rev 208:17–31. https://doi.org/10.1007/s11214-015-0227-y
Kitazato K, Milliken RE, Iwata T et al (2019) The surface composition of asteroid 162173 Ryugu from Hayabusa2 near-infrared spectroscopy. Science 364:272–275. https://doi.org/10.1126/science.aav7432
Matsumoto K, Noda H, Ishihara Y et al (2020) Improving Hayabusa2 trajectory by combining LIDAR data and a shape model. Icarus 338:113574. https://doi.org/10.1016/j.icarus.2019.113574
Mizuno T, Kase T, Shiina T et al (2017) Development of the laser altimeter (LIDAR) for Hayabusa2. Sp Sci Rev. https://doi.org/10.1007/s11214-015-0231-2
Noda H, Matsumoto K, Senshu H, Namiki, N (2019) Alignment Determination of the Hayabusa2 Laser Altimeter (LIDAR). In: Abstracts of 16th Annual Meeting of Asia Oceania Geosciences Society, Suntec Singapore Convention & Exhibition Centre, 28 July–2 Augst 2019
Ono G, Tsuda Y, Akatsuka K et al (2016) Generalized attitude model for momentum-biased solar sail spacecraft. J Guid Control Dyn. 39(7):1491–1500. https://doi.org/10.2514/1.g001750
Otsubo T, Matsuo K, Aoyama Y et al (2016) Effective expansion of satellite laser ranging network to improve global geodetic parameters. Earth Planets Space 68:65. https://doi.org/10.1186/s40623-016-0447-8
Sugita S, Honda R, Morota T et al (2019) The geomorphology, color, and thermal properties of Ryugu: implications for parent-body processes. Science 364:eaaw0422. https://doi.org/10.1126/science.aaw0422
Suzuki H, Yamada M, Kouyama T et al (2018) Initial inflight calibration for Hayabusa2 optical navigation camera (ONC) for science observations of asteroid Ryugu. Icarus 300:341–359. https://doi.org/10.1016/j.icarus.2017.09.011
Tatsumi E, Kouyama T, Suzuki H et al (2019) Updated inflight calibration of Hayabusa2’s optical navigation camera (ONC) for scientific observations during the cruise phase. Icarus 325:153–195. https://doi.org/10.1016/j.icarus.2019.01.015
Terui F, Ogawa N, Mimasu Y et al (2013) Guidance, navigation and control of hayabusa2 in proximity of an asteroid. Adv Astronaut Sci 149:651–663
Tsuda Y, Yoshikawa M, Abe M et al (2013) System design of the hayabusa 2-asteroid sample return mission to 1999 JU3. Acta Astronaut 91:356–362. https://doi.org/10.1016/j.actaastro.2013.06.028
Turyshev, VG (2011) NASA’s deep space network: current status and the future. http://lnfm1.sai.msu.ru/~turyshev/lectures/lecture_10.1-DSN-Present-Future.pdf. Accessed 15 April 2020
Watanabe S, Hirabayashi M, Hirata N et al (2019) Hayabusa2 arrives at the carbonaceous asteroid 162173 Ryugu—A spinning top–shaped rubble pile. Science 364:268–272. https://doi.org/10.1126/science.aav8032
Acknowledgements
We would like to thank the two anonymous reviewers for their constructive comments. The comments have helped us significantly improve our paper.
Funding
This study was supported by Japan Society for the Promotion of Science (JSPS) Core-to-Core program “International Network of Planetary Sciences”.
Author information
Authors and Affiliations
Contributions
Preparation of the manuscript: KYa. Data analysis: KYa, KM. Software development: TO. Methodology: KM, TO, HT. Interpretation: KYa, KM, TO, HT, HI, MY. Administration of LIDAR science team: NN. LIDAR operation: KYa, KM, HN, NN, HI, HS, TM, NH, RY, YI, HA, SA, FY, AH, SS, SO, STs, KA, MS. Critical operation of the spacecraft: NO, GO, YM, KYo, TT, YT, AF, TY, SK. Science operation of the spacecraft: HT, YY, TY. Administration of Hayabusa2 project: MY, SW, STa, FT, SN, TS, YT. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Additional file 1: Table S1.
Fully normalized spherical harmonic coefficients of the gravity field model of Ryugu up to degree and order 10 obtained from the shape model SHAPE_SPC_3M_v20181109 based on the assumption of the globally constant density.
Additional file 2: Table S2.
The AIT data used in this study.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yamamoto, K., Otsubo, T., Matsumoto, K. et al. Dynamic precise orbit determination of Hayabusa2 using laser altimeter (LIDAR) and image tracking data sets. Earth Planets Space 72, 85 (2020). https://doi.org/10.1186/s40623-020-01213-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-020-01213-2