Earthquake Forecast Testing Experiment in Japan (II)
- Article
- Open access
- Published:
Statistical forecasts and tests for small interplate repeating earthquakes along the Japan Trench
Earth, Planets and Space volume 64, pages 703–715 (2012)
Abstract
Earthquake predictability is a fundamental problem of seismology. Using a sophisticated model, a Bayesian approach with lognormal distribution on the renewal process, we theoretically formulated a method to calculate the conditional probability of a forthcoming recurrent event and forecast the probabilities of small interplate repeating earthquakes along the Japan Trench. The numbers of forecast sequences for 12 months were 93 for July 2006 to June 2007, 127 for 2008, 145 for 2009, and 163 for 2010. Forecasts except for 2006–07 were posted on a web site for impartial testing. Consistencies of the probabilities with catalog data of two early experiments were so good that they were statistically accepted. However, the 2009 forecasts were rejected by the statistical tests, mainly due to a large slow slip event on the plate boundary triggered by two events with M 7.0 and M 6.9. All 365 forecasts of the three experiments were statistically accepted by consistency tests. Comparison tests and the relative/receiver operating characteristic confirm that our model has significantly higher performance in probabilistic forecast than the exponential distribution model on the Poisson process. Therefore, we conclude that the occurrence of microrepeaters is statistically dependent on elapsed time since the last event and is not random in time.
1. Introduction
Earthquake periodicity and seismic gaps have been used for long-term forecasts of large earthquakes in various regions (e.g., Imamura, 1928; Sykes, 1971; Kelleher, 1972; Kelleher et al., 1973; McCann et al., 1979; Working Group on California Earthquake Probabilities (WGCEP), 1988, 1990, 1995, 2003; Nishenko, 1991; Earthquake Research Committee (ERC), 2001; Matsuzawa et al., 2002; Field, 2007; Field et al., 2009). McCann et al. (1979) gave forecasts for specified ranked categories of earthquake potentials for most of the Pacific Rim. Nishenko (1991) presented the first global probabilities of either large or great interplate earthquakes in 97 segments of simple plate boundaries around the circum-Pacific region during the next 5, 10, and 20 years, in terms of conditional probability based on elapsed time since the last event and mean recurrence time with a lognormal distribution model. Rigorous tests of Nishenko’s forecasts were conducted by Kagan and Jackson (1995) for 5 years and by Rong et al. (2003) for 10 years by using the seismic catalogs of the Preliminary Determination of Epicenters (PDE) of the U.S. Geological Survey and the Harvard Centroid Moment Tensor (CMT). They statistically rejected Nishenko’s forecasts with the number test (N-test), the likelihood test (L-test), and the likelihood ratio test (R-test). The predicted events in both periods were too numerous to result from random variation. As reasons for failure, they suggested biasing of the estimated earthquake rate and excluding effects of open intervals before the first event and after the last event.
Davis et al. (1989) indicated that parameter uncertainties affect seismic potential estimates strongly for some distributions (e.g., the lognormal) and weakly for the Poisson distribution. The method used by Nishenko is too crude to reflect the parameter estimation errors derived from the small number of samples on the probabilities. Official forecasts by WGCEP and ERC have not yet been tested statistically, as the forecast periods are not yet over.
In this paper, we study the predictability of recurrent earthquakes, applying sophisticated methods based on the Bayesian approach or small sample theory with lognormal distribution. The small repeating earthquakes (SREs) used in this study occur on the plate boundary in the same condition for large interplate earthquakes. The SRE data is much more suitable than large recurrent event data for experiments of prospective probabilistic forecasts for three reasons: (1) events are objectively qualified and accurate in time; (2) the recurrence intervals are short; and (3) the catalog of events is compiled based on a stable observation network and contains many sequences to test forecasts statistically.
More than 1000 characteristic sequences or clusters of SREs with nearly identical waveform have been found near the east coast of NE Japan since 1984 (36.5–41.5 deg. N) or 1993 (41.5–43.5 deg. N and 34.5–36.5 deg. N) (Igarashi et al., 2003; Uchida et al., 2003). These repeaters in a cluster are assumed to occur on the same small asperity surrounded by an aseismic creeping zone on the plate boundary. The forecast bin specifying an event may be smaller in volume of location and in focal mechanism, but the magnitude range for a sequence may be larger than those for Regional Earthquake Likelihood Models (RELM) by Schorlemmer et al. (2007) and for the Collaboratory for the Study of Earthquake Predictability (CSEP, Jordan, 2006). We estimated the probabilities for repeaters in the forecast period of a year using a Bayesian model with lognormal distribution. There were 93 sequences for July 2006 to June 2007, 127 for 2008, 145 for 2009, and 163 for 2010 that were selected for the forecast. The repeaters occurred from 1993 until the forecast time were used to calculate the forecast probability. The forecast sequences consisted of five events or more. With the exception of the results of the first experiment (2006–2007), those probabilities were posted on a web site for impartial forecast and testing.
Comparing forecasts with a seismic catalog on repeater data, we tested probabilities with not only N- and L-tests but also with the test of Brier score (Brier, 1950). We pay attention to whether the next qualifying event in the sequence will occur in the forecast period or not, regardless the event timing within the forecast period. Alternative forecasts were computed with the lognormal distribution model based on the small sample theory and the exponential distribution model based on the Poisson process. The three models were compared using the R-test and the test of difference in Brier scores.
2. Theory
We assume that (n + 1) events of a sequence have occurred, separated by n time intervals T i , and that the time elapsed since the last event is T p . The unknown recurrence interval from the last event to the upcoming one is denoted as T n +1.
In the lognormal distribution model on a renewal process, the common logarithms of recurrence interval, X
i
= ln(T
i
), follow a normal distribution, N(µ, σ2). Symbols and probability density functions (PDFs) of some distributions are listed in Table 1. The sample mean,  , and sample variance,
, and sample variance,  , are determined from observed data at the forecasting time (T
p
).
, are determined from observed data at the forecasting time (T
p
).
If population parameters are known, it is very easy to calculate the probability, P q (T p , T p + ΔT), for the event in the forecast period with the conditional probability,

where F N is the cumulative distribution function (CDF) of a normal distribution, ΔT is the length of the forecast period, x p = ln(T p ), and x f = ln(T p + ΔT). However, it is actually very difficult to find the accurate parameters for a population from small samples, and it is better to regard them as unknown parameters.
2.1 Bayesian approach
Maximum likelihood estimates may be biased when there are few samples and a wide range of values are consistent with the observation (Davis et al., 1989). We will not determine the parameters with the maximum likelihood method or the least square method. Instead, we directly estimate the conditional probabilities, P q , in Eq. (1) by the Bayesian approach.
The likelihood function including the open-ended interval is given as

According to Bayes’ theorem, the PDF for parameters, h(µ, σ2), is given as

where π(µ,σ2) is the prior distribution for parameters. Here, P q is not a specified value but a random variable. The CDF for P q is given as

Where 0 ≤ p ≤ 1. Integration of this formula is remarkably complicated; thus, we use the average of conditional probability,  , as the probability of a qualifying event, written as
, as the probability of a qualifying event, written as


Let us consider here the prior distribution. We adopted the uniform prior distribution for parameter µ since it varies in an infinite interval, −∞ <µ< ∞.For σ2 varying in a semi-infinite interval, 0 <σ2< ∞, two types were studied. One is a natural conjugate prior distribution, inverse gamma, Γ R (ϕ,ζ), and the other is the non-informative prior distribution, inverse of σ2, proposed by Jeffreys (1961). Parameter ϕ indicates shape and ζ indicates scale for inverse gamma.
By using an inverse gamma prior distribution, Eq. (5) is written as

As terms of f
N
and f
R
are PDFs of the normal and inverse gamma distributions, they become unity with integration of µ and σ2 over the whole interval. The probability,  ,in Eq. (4) is finally given as
,in Eq. (4) is finally given as

This formula means that the variable  follows t -distribution with n + 2ϕ − 1 degrees of freedom, and conditional probability is given by Eq. (1) for this variable.
follows t -distribution with n + 2ϕ − 1 degrees of freedom, and conditional probability is given by Eq. (1) for this variable.
For the prior distribution of (σ2)−m for σ2,  is calculated as
is calculated as

Jeffreys’ non-informative prior distribution corresponds to m = 1 (Jeffreys, 1961), and we expect that the variable of  obeys t-distribution with n − 1 degrees of freedom.
obeys t-distribution with n − 1 degrees of freedom.
2.2 Small sample theory
Suppose n + 1 random variables X
i
= ln(T
i
), i= 1,…, n + 1 obey a normal distribution N(µ, σ2) and take the variables for mean and variance of n variables,  and
and  . The following properties are well-known in statistics (e.g., Wilks, 1962).
. The following properties are well-known in statistics (e.g., Wilks, 1962).
-
(1)
The variable
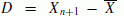 follows N (0,(n + 1)σ2n).
follows N (0,(n + 1)σ2n). -
(2)
The variable nS2/σ2 follows a chi-squared distribution with n − 1 degrees of freedom.
-
(3)
The variable
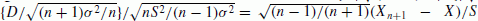 follows a t-distribution with n − 1 degrees of freedom.
follows a t-distribution with n − 1 degrees of freedom.
At forecasting time, we have n data, and the mean and variance of samples,  and s2, corresponding to
and s2, corresponding to  and S2, can be calculated. Thus, we naturally expect that the variable
and S2, can be calculated. Thus, we naturally expect that the variable  follows a t-distribution with n − 1 degrees of freedom. Therefore, the probability based on the small sample theory (exact sampling theory) is calculated by the Bayesian approach with Jeffreys’ noninformative prior distribution.
follows a t-distribution with n − 1 degrees of freedom. Therefore, the probability based on the small sample theory (exact sampling theory) is calculated by the Bayesian approach with Jeffreys’ noninformative prior distribution.
2.3 Exponential distribution model
If the event occurs uniformly and randomly, the probability of an event does not depend on the elapsed time since the last event, and the recurrence interval between successive events is distributed exponentially. Conditional probability is given by  , where
, where  is the average of observed recurrence intervals.
is the average of observed recurrence intervals.
3. Small Repeating Earthquakes
It has been pointed out that SREs are caused by the repeated rupture of small asperities within the creeping zone of a fault plane (e.g., Nadeau et al., 1995; Igarashi et al., 2003; Uchida et al., 2003). We use the waveform similarity of earthquakes with a magnitude of 2.5 or larger to identify repeaters in the subduction zone between the Japan Trench and the east coast of NE Japan. Maximum magnitude is practically about 5 mainly owing to the employed waveform similarity threshold that is applicable for small earthquakes. The SRE was objectively selected by the threshold of waveform coherence in a 40-second waveform that contains both P and S phases. Details of the methods for identifying SRE and for compiling the SRE catalog are described by Uchida et al. (2009).
SREs are more suitable for the prospective forecasts than previous studies (e.g., Nishenko, 1991), because the events are objectively identified, the occurrence times are accurate, the recurrence intervals are much shorter, and many sequences have been found. We applied three criteria for SRE sequences for forecasting: (1) five or more events occurred from 1993 until the forecast time, (2) the averaged magnitude is 2.75 or larger and less than 4.5, and (3) the number of possible aftershocks of the 2003 Off Tokachi earthquake (September 26, 2003; M 8.0) and the 1994 Off Sanriku earthquake (December 28, 1994; M 7.6) are less than one third of the events in the sequence. Aftershock activity includes many SREs (Uchida et al., 2003, 2009; Chen et al., 2010), but the physical conditions for the earthquake occurrence for the period are thought to be complicated and unstable due to the existence of afterslip or stress interactions. We regarded SREs as possible aftershocks that occurred in the areas of “Off Tokachi” in the period from the main shock through March 31, 2005 and “Off Sanriku” in the period from the main shock through January 31, 1996 (Fig. 1). These three criteria were chosen considering the stability of seismic observation, the lower magnitude limit of clear waveform records for offshore events, and the influence of nearby earthquakes that cause changes in the loading rate. In this study, small repeaters are thought to occur by the same process as large interplate earthquakes. Exclusion of aftershocks can exclude repeaters under the strong effect of nearby much larger earthquake that is not expected for large earthquakes.
Distribution of the SRE clusters. The colored symbols indicate sequences of the 2010 forecast, but the gray ones are not used, due to the criteria discussed in the main text. The area of “OFF TOKACHI” denotes the possible aftershock area for the 2003 Off Tokachi earthquake (September 26, 2003, M 8.0), and that of “OFF SANRIKU” denotes the possible aftershock area for the 1994 Off Sanriku earthquake (December 28, 1994, M 7.6). The stars denote the epicenters of the main shocks.
Ninety-three sequences satisfied the above criteria for the forecast on July 1, 2006; 127 for that on January 1, 2008; 145 for that on January 1, 2009; and 163 for that on January 1, 2010. Figure 1 presents the distribution of SRE clusters having four or more events from 1993 to 2009 with an average of M 2.5 or larger. Clusters with colored symbols (except small gray symbols) were used for the 2010 forecast. The SREs are distributed in the subduction zone off Kanto to Hokkaido. The averaged magnitudes of forecast sequences are between 2.75 and 4.26. Figure 2 presents the frequency distribution of the number of events in each sequence for the 2010 forecast. Two-thirds of the 163 sequences have seven SREs or less, which is fairly small for statistical estimation of probability. The range of averaged sequence recurrence interval is from 0.83 to 3.84 years and the coefficient of variations, ratio of standard deviation to averaged interval, is 0.47 in average and less than 0.5 for about 60 percents of sequences for 2010.
4. Forecasts and Observations
We tried to estimate the probabilities of SRE sequences on the plate boundary along the Japan Trench. Their locations are indicated in Fig. 1. The fundamental values of forecasts (e.g., the number of sequences) are listed in Table 2. The prospective forecast probabilities for one year were posted on the web site1 in July of 2008, April of 2009, and March of 2010 for impartial testing.
We used the following three models for calculating probabilities and statistical testing.
-
LN-Bayes: A Bayesian approach for lognormal distribution of the recurrence interval with an inverse gamma prior distribution. The probability forecast by this model is given by Eq. (6). The parameters of inverse gamma were ϕ = 2.5 and ζ = 0.44 (Okada et al., 2007) for the two earlier trials. They were changed to ϕ = 1.5 and ζ = 0.15 for the two later trials, based on the R-test result for the 2008 probabilities calculated by LN-Bayes and by LN-SST. Determination of these parameters is briefly explained in Appendix.
-
LN-SST: Lognormal distribution model based on the small sample theory. The probability forecast by this model is given by Eq. (7). This is an alternative model to determine consistency with LN-Bayes.
-
EXP: Exponential distribution model based on the Poisson process. The probability of an event is independent of the elapsed time since the last event. This is the alternative model to compare with the two time-dependent models, LN-Bayes and LN-SST.
The prospective probabilities for SREs in 2008 are indicated in Fig. 3(a), and qualifying events are indicated in Fig. 3(b). The red circles denote earthquake occurrence, and the blue circles represent the non-occurrence of earthquake. There are many sequences with high probability near the east coast of northern Honshu, Japan, and most of them included qualifying events during the forecast period. There is a gap of SRE sequences southeast off Hokkaido, since we removed the clusters in which one-third or more events are regarded as possible aftershock of the 2003 Off Tokachi earthquake and the 1994 Off Sanriku earthquake, as explained earlier.
For 2009 forecasts (Fig. 4), as many as 23 qualifying repeaters occurred to the south of 38°N, which is remarkably more than the number expected from prospective probabilities (17.1) for the region. In this area, the rate of SRE sequences with low probability increased in the 2010 forecasts (Fig. 1), because probability just after an earthquake in a sequence is low for the lognormal distribution based on the renewal process.
5. Forecast Verification
Three tests (N-, L-, and R-tests) were applied by Kagan and Jackson (1995) and Rong et al. (2003) to the probabilistic forecasts by Nishenko (1991). Those tests are a fundamental procedure to evaluate the rates of earthquakes forecast by various models submitted to the Regional Earthquake Likelihood Models Center (Schorlemmer et al., 2007). Moreover, we use different verification methods presented by Jolliffe and Stephenson (2003) for the probabilistic forecasts of binary events. In the following sections, we assume that events are independent from seismic activities in other clusters.
5.1 Reliability and resolution
We examined the reliability and resolution of the forecasts by the LN-Bayes, LN-SST, and EXP models. Those forecasts are divided into ten classes depending on the probability. Figure 5 depicts resulting frequencies and probabilities that are summed for the three 12-month forecasts from 2006 to 2009. The total expectation of events (gray bars) and the observed number of qualifying SREs (black bars) are comparable for the three models.
Frequencies of forecast sequences (left white bars), the expected number of sequences filled with qualifying events (the sum of forecast probabilities, central gray bars), and the actual number of observed qualifying events (right black bars) for every 10% range of probabilities for three trials (forecast period: 2006–2007, 2008, and 2009) for the LN-Bayes (top), the LN-SST (middle), and the EXP (bottom) models. Ns: the number of all forecast sequences, Nq: the number of all sequences filled with qualifying event, E(Nq): sum of all probabilities (expectation of Nq), MLL: mean of log-likelihood, and BS: Brier score.
The reliability (Rel) and resolution (Res) are defined as follows (Toth et al., 2003);

where K is the number of classes, and n
k
,  and
and  are the number of forecasts, the averaged probability and the rate of event occurrence for k-th class, respectively, and
are the number of forecasts, the averaged probability and the rate of event occurrence for k-th class, respectively, and  is event occurrence rate for all forecasts. The smaller the reliability is, the better the forecast is. And the larger the resolution is, the better the forecast is. The resolution is independent of reliability.
is event occurrence rate for all forecasts. The smaller the reliability is, the better the forecast is. And the larger the resolution is, the better the forecast is. The resolution is independent of reliability.
The values of reliability are 0.00091 for LN-Bayes, 0.00105 for LN-SST, and 0.0019 for EXP. And the resolutions are 0.0590 for LN-Bayes, 0.0616 for LN-SST, and 0.0254 for EXP. These results indicate that forecast probabilities by those models are not so biased and that their reliability may be fairly good. The forecast by the LN-Bayes model is slightly better in reliability but worse in resolution than those by the LN-SST model. The gray bars in the top panel in Fig. 5 are slightly more consistent with the black ones and are more concentrated than those in the middle panel. The EXP model is much lower in resolution than others, as shown in bottom panel in Fig. 5 the probabilities are apt to gather in some ranges.
5.2 Relative/Receiver Operating Characteristic
The Relative/Receiver Operating Characteristic (ROC) is a signal detection curve over a range of different probability decision thresholds (e.g., Jolliffe and Stephenson, 2003). Suppose that we issue an alarm for every case of probability higher than the threshold. The hit rate is the ratio of the number of hit alarms and all SRE sequences with a qualifying event, and the false alarm rate is the ratio of the number of false alarms and all sequences without a qualifying event. Both rates increase from 0 to 1 as the threshold probability changes from 1 to 0. In Fig. 6, the horizontal axis indicates the false alarm rate, and the vertical axis indicates the hit rate for the three 12-month forecasts from 2006 to 2009. The curve located in the upper left zone indicates better forecasts, and that near the diagonal line corresponds to random forecasts. This figure confirms that forecasts by the EXP model are better than random forecasts, as the model uses information on the average of observed recurrence interval. The LN-Bayes and LN-SST models are comparable in predictability and are remarkably better than the EXP model.
(a) ROC curves for all probabilistic forecasts (i.e., 365 forecasts) produced by the three models in the trials of 2006–2007, 2008, and 2009. The black diagonal line indicates the forecasts by random distribution, the purple curve denotes those by the EXP model, the green curve denotes those by the LN-SST model, and the red curve denotes those by the LN-Bayes model.
5.3 Consistency test
We use three scores and related tests, based on the total number of qualifying events (N-test), the likelihood score (L-test), and the Brier score (BS-test) (Brier, 1950). For the consistency test, the score of observation data is compared with the theoretical score distribution that is computed from the forecast probabilities. Those scores and the test results are summarized in Table 2.
The theoretical distribution of the frequency of sequences with qualifying event, N q is numerically calculated with the iteration formula

where p
n
+1 is the probability of the qualifying event of the (n + 1)-th forecast, and Pr( ) is the probability for k of n + 1 sequences to include qualifying events.
) is the probability for k of n + 1 sequences to include qualifying events.
Scores of log-likelihood, LL, and Brier, BS, for n forecasts for binary events are given as

where p i is the forecast probability that the i-th sequence will include a qualifying event; c i is equal to 1 if the event occurs, and is zero otherwise.
The theoretical distribution of LL is also numerically calculated with the iteration formula

, where i = 1 corresponds to a qualifying event, i = 0 to otherwise, and j = 0, 1, …, jmax, x0,n+1 = ln(1 − p n +1), and x1,n+1 = ln(p n +1). The number of score values, jmax, for n forecasts may rapidly increase as fast as 2n. When x j,n and x k,n are equal or very close to each other and their probabilities are very small, we replace them by a weighted mean of two, x l,n , to decrease the number:

The theoretical distribution of BS is numerically calculated by a similar procedure for the LL score.
The expected frequency (number of events) of 56.1 for 2008 determined by the Bayesian model is very close to that of observed qualifying events (56), but is somewhat smaller than the actual frequency for other periods. The other two models estimated a smaller number than the LN-Bayes model. Figure 7 presents an example of the N-test, which compares the theoretical distribution for the 365 forecasts of the three trials with the observed frequency (177 qualifying events, vertical dashed line). The observed number corresponds to 0.984 in theoretical CDF. This result means that the expected number, E(N), is too small to accept those forecasts, and they are rejected statistically at a significance level of 0.95 but accepted at a level of 0.99.
N-test for 365 forecasts of three trials by the LN-Bayes model. The black curve indicates the theoretical distribution of the frequency of qualifying events calculated from forecast probabilities, and the vertical dashed line indicates the observed frequency of qualifying events. Ns is the number of forecast sequences and Nq is the number of sequences filled with qualifying event in the forecast period.
Examples of the L-test and BS-test are depicted in Figs. 8 and 9 for the forecasts of three experiments from 2006 to 2009, respectively. Our probabilities are accepted at the 0.95 significance level. We denote the mean of log-likelihood for a single forecast with MLL (= LL/n). For better forecasts, the scores of LL and MLL are larger, while the BS score is smaller. The result of the test with the MLL score is the same as that of the L-test. The MLL and BS scores produced by the LN-Bayes model, listed in Table 2 for three trials, are close to those produced by the LN-SST model and are remarkably better than those by the EXP model. The scores for the 2009 forecasts are somewhat worse than the former two trials (Table 2).
L-test for 365 forecast probabilities of three trials produced by the LN-Bayes model. The curved line denotes the theoretical distribution of the total log-likelihood, LL, and the vertical dashed line denotes its observed score. The horizontal lines indicate the points of 0.05 and 0.95 of the cumulative probability used for testing. Ns is the number of forecasts.
The scores of MLL and BS may be used to compare the forecasts with those in a different number or type. For example, Fig. 10 compares our forecasts for SREs with those for precipitation at Tokyo produced by the Japan Meteorological Agency. Their precipitation forecast is similar to ours if we replace earthquake with precipitation. The forecast is the probability of rain (earthquake) and the result is whether it rained (earthquake occurred) or not. The scores of SRE forecasts for 2006–2007 and 2008 were comparable to those for precipitation several day forecasts, but the 2009 forecasts were worse than the weather forecasts.
5.4 Comparison test
We statistically compare the forecasting model (H1) and the alternative model (H0) by the R-test, which is based on the differences in LL, and the dBS-test, which is based on the differences in BS. Theoretical score distributions used for these tests are numerically computed by a procedure similar to that applied for LL.
Figure 11 presents the results of the R-test for the LN-Bayes model (H1) and the EXP model (H0) for 365 forecasts of three trials from 2006 to 2009. If H0 is correct, the difference of the log-likelihood, R = LH1 − LH0, is theoretically distributed as the blue curve. However, it does not fit the observed value of R = 34.5, therefore, H0 (EXP model) is statistically rejected. In contrast, the theoretical distribution for H1 fits the observed value; thus, H1 is statistically accepted. Hence, the forecast model H1 is considered to be significantly better than the alternative model H0 at a significance level of 0.95.
The results of the R-test for the LN-Bayes model (H1) and the LN-SST model (H0) are depicted in Fig. 12. Both models are rejected at a significance level of 0.95 but accepted at a level of 0.99. Figure 13 presents the result of the dBS-test, in which the LN-Bayes model is statistically better than the LN-SST model, though the difference in scores is very small.
All results of R- and dBS-tests for the three trials are summarized in Table 3. Here, AC indicates that the score is accepted by N-, L-, or BS-test at a significance level of 0.95; RJ indicates that it is rejected at the 0.99 level; and UD indicates that it is rejected at the 0.95 level but accepted at the 0.99 level. As a whole, the EXP model is quite significantly worse than the other two models.
6. Discussion
To evaluate the prospective forecasts, we consider the following four sets of forecasts: (1) 93 probabilities for the first trial (July 2006 to June 2007), (2) 127 probabilities for the second trial (2008), (3) 145 probabilities for the third trial (2009), and (4) 365 combined probabilities for all three trials. The results of the fourth trial (2010) are not available for evaluation because the forecast period was not over at the time of the submission of this paper. Among these sets, (1), (2), and (4) were accepted by consistency tests, the L-test, and the BS-test (Table 2). However, the forecasts of (3) were rejected statistically, as we will discuss later.
The recurrence interval itself is important for forecast. If the interval is less than the forecast period, the probability for the repeater is inevitably high. The ROC in Fig. 6 shows that the EXP model based on Poisson process taking the averaged sequence recurrence interval into account is better than the random forecast. Results of R- and dBS-tests (Fig. 11 and Table 3) indicate that the LN-Bayes and LN-SST models dependent on elapsed time since the last event are significantly better than the EXP model. The ROC curves depicted in Fig. 6 also suggest that these models have much higher performance than the EXP model for estimating probabilities (Figs. 5 and 6 and Tables 2 and 3). Therefore, the repeaters on the plate boundary along the Japan Trench are significantly dependent on elapsed time since the last event and are not random in time. However, it is presumed that the inverse gamma prior distribution used in the LN-Bayes model is slightly more effective for forecast repeaters, since the differences between the consistency scores of the LN-Bayes and the LN-SST models are very small.
Missing event, especially last one, has significant effect on the forecast probability for the relevant sequence. We collected the SRE by comparing waveform of events recorded at the same station which were listed in the catalog maintained by the Japan Meteorological Agency for 2.5 or larger in magnitude. Nanjo et al. (2010) estimated that the completeness magnitude, Mc, for recent event was 1.5 or smaller in the coastal zone and between 2.0 and 2.5 in the offing area near Japan Trench. Mc before the deployment of modern dense observation network in 2002 for the northeastern Japan was about 0.5 larger than the recent one. The ratio of signal to noise is smaller for the events in the distant offing than the coastal zone and the fluctuation of noise level also affect the detectability of the small repeating earthquake. Therefore we assume that some older events near the Japan Trench might be missed from our SRE catalog. However the most sequences in coastal zone seem to be nearly complete and our results are considered to be in high quality as a whole as shown in the data quality estimation at off Sanriku region (Uchida et al., 2005).
The forecasts by Nishenko (1991) for large characteristic interplate earthquakes around the circum-Pacificregion were rigorously tested by Kagan and Jackson (1995) and Rong et al. (2003), and were statistically rejected. They suggested two reasons, the biasing of rate and the effects of excluding open intervals. We also assume that the model in the previous study is too crude for the small number of data. The SRE and the models employed in this study can adequately deal with these problems. The SRE selected on the basis of waveform similarity excludes bias by the selection of sequence; the models using the Bayesian approach and small sample theory adapt fairly well to small samples and the open-ended interval. We also suggest that the common variance parameter, σ = 0.215, used by Nishenko is probably too small. In our Bayesian model, the mean of prior distribution for σ2 is close to 0.3, and the expectation of σ exceeds 0.215 for most sequences.
As the SREs occur in the same geophysical condition for the large/great interplate earthquakes, it is likely that our method is applicable for those recurrent events. A preliminary prior distribution for large events has been proposed by Okada et al. (2007). However it is fairly difficult to test the prospective forecasts for the large/great earthquake due to much longer time interval and small number of recurrent events for each sequence. Moreover we have to pay attention to the uncertainty and errors of old data derived from historical documents or geological surveys. Therefore it might be fruitful to perform the prospective forecast experiments for the moderate recurrent earthquakes with 4 to 7 in magnitude recorded with seismological instruments and to test them with observation data in advance of the experiment for large events.
Next we discuss why the consistency tests rejected our forecasts of 2009. The distribution patterns of clusters in Figs. 1, 3, and 4 in the northern part are somewhat different from those in the southern part. The SRE sequences are crowded near the coast in the northern part and widely distributed in the southern part. In the northern part to the north of 38°N, the score of MLL is −0.614 and that of BS is 0.218 for 97 sequences of the 2009 forecasts, and the expected number of qualifying events of 44.1 is close to the observation of 47. In the southern part, for 48 sequences the score of MLL is as bad as −0.715 and that of BS is as bad as 0.247. Furthermore, the expected number of 17.1 is considerably smaller than the observed 23. Consistency scores for the southern part are considerably worse than those for the northern part.
We assume that worse results in consistency for the southern part are due to a large and long-term slow slip event that is not considered in the present model. In 2008, M 7.0 and M 6.9 interplate earthquakes occurred on the plate boundary of the southern part of the study area (Fig. 14). The Geographical Survey Institute (2010) estimated from GPS observation that the M 7.0 earthquake on May 8, 2008, had triggered a wide and long-term aseismic slip in this district corresponding to 6 to 12 cm/year (Fig. 14). The afterslip area was much wider than the co-seismic slip area of the M 7.0 event, 25 km × 25 km (Nagoya University, 2008) and the foreshock and aftershock area extended 40 km × 90 km. Co-seismic slip was estimated to be 1.7 m in maximum. This is one of the largest earthquakes in the last 80 years in the rectangle part drawn with a red dotted line in Fig. 14. Mishina et al. (2009) observed a strain change related to the afterslip of the M 6.9 earthquake on July 19, 2008, using a coastal borehole strain meter. Uchida et al. (2008) applied cumulative slip analysis for SRE sequences and suggested that the aseismic slip was about 3 cm/year before the M 7.0 event and accelerated in a 300 km-long region near the Japan Trench, which encompasses both the M 7.0 and M 6.9 earthquakes. Therefore, we assume that the slow slip in the large area must be related to the high activities of SREs as well as the occurrence of several M 6+ earthquakes in that part.
Activities of SRE in the southern part in 2009. The circles indicate that the qualifying SRE occurred in the forecast period of 2009, and the triangles indicate that none occurred in 2009. The stars denote large earthquakes of M 6.0 and larger. The black contour lines indicate the main slip part from January 19 through March 19, 2009, estimated from GPS observation (Geographical Survey Institute, 2010). The 2008 Off Ibaraki earthquake of M 7.0 is one of the largest events in the rectangle part drawn with the red dotted line.
We also must pay more attention to regional differences and clustering of SRE activities. The frequency of qualifying events within every six months from 1993 to 2009 is 36.0 on average for the 163 sequences used for the 2010 forecasts, and their variance is 68.9, which is much larger than that of Poisson distribution with a mean of 36.0. It is plausible that some variation in SRE activity is caused by the coherent occurrence of repeaters among characteristic sequences, the effects of which are neglected in our models not only for forecast but also testing.
The Brownian Passage Time (BPT) distribution model is frequently used for recurrence interval as a physically based model (e.g., Ellsworth et al., 1999; ERC, 2001; Matthews et al., 2002; WGCEP, 2003). Matthews et al. (2002) discuss the characteristic of Brownian relaxation oscillator and BPT distribution in detail and show the physical interpretation of parameters and the effect of stepwise stress change on recurrence time. But it was rather difficult for us to apply Bayes’ theorem to this distribution. We tried to estimate probabilities, using parameters determined by the maximum likelihood method from the observed data. We failed to obtain the conditional probabilities for some sequences. In several sequences, the open interval from the last event was so long that the CDF was abnormally high. When the sequence contained a doublet (earthquakes with very short interval), the parameters could not be determined by using likelihood with an open-ended interval denoted by Eq. (2). In one case, we could not calculate CDF for a BPT distribution due to an overflow in computation. The BPT distribution may be suitable for forecast based on the declustered data. We also tried to forecast probabilities with other distributions for the recurrence interval (e.g., Weibull and gamma on the large sample theory); however, the probability for some sequences could not be computed normally, due to the difficulties mentioned above. The probabilities by these models exclusive of abnormal cases were worse than those by LN-Bayes and LN-SST. Therefore, we did not use those distributions in present study, just lognormal and exponential distributions, for forecasting probabilities.
7. Conclusion
We theoretically formulated a method to calculate the conditional probability of a forthcoming recurrent event, using the Bayesian approach of a lognormal distribution model with the uniform prior distribution for the mean of the logarithm of recurrence interval and inverse gamma for its variance (LN-Bayes), and the model on the small sample theory (LN-SST). The probabilities forecast by both models are given by simple equations including t-distribution function.
The probabilities forecast by the LN-Bayes model for SREs in the subduction zone along the Japan Trench are estimated for 12 months in 2006–07, 2008, and 2009. The results indicate that all forecasts except that for 2009 were so good that they passed the N- L- and BS-tests statistically. The 2009 forecasts were rejected by the L- and BS-tests, probably due to a large and long-term afterslip event on the plate boundary triggered by M ∼ 7 earthquakes in 2008. The MLL and BS scores of the SRE forecasts of two former experiments were comparable to those for precipitation several day forecasts at Tokyo, but the 2009 SRE forecasts were worse than the weather forecasts.
Comparison tests, the R-test and dBS-test, for all 365 forecasts in the three experiments indicate that the LN-Bayes model based on the renewal process had significantly higher performance than the EXP model based on the Poisson process. The ROC curve also indicates that the LN-Bayes model is remarkably better than the EXP model. Therefore, we conclude that the SREs on the plate boundary are statistically dependent on elapsed time since the last event and are not random in time. However, we assume that the inverse gamma prior distribution for variance used in the LN-Bayes model is slightly more effective than the LN-SST model, although the consistency scores of our experiments are fairly close for the two models.
References
Brier, G. W., Verification of forecasts expressed in terms of probability, Month. Weather Rev., 78, 1–3, 1950.
Chen, K. H., R. Buergmann, R. M. Nadeau, T. Chen, and N. Lapusta, Postseismic variations in seismic moment and recurrence interval of repeating earthquakes, Earth Planet. Sci. Lett., 299, 118–125, doi:10.1016/j.epsl.2010.08.027, 2010.
Davis, P. M., D. D. Jackson, and Y. Y. Kagan, The longer it has been since the last earthquake, the longer the expected time till the next?, Bull. Seismol. Soc. Am., 79, 1439–1456, 1989.
Earthquake Research Committee, Regarding methods for evaluating longterm probability of earthquake occurrence, 48 pp, 2001 (in Japanese).
Ellsworth, W. L., M. V. Matthews, R. M. Nadeau, S. P. Nishenko, P. A. Reasenberg, and R. W. Simpson, A physically-based earthquake recurrence model for estimation of long-term earthquake probabilities, U.S. Geol. Surv., Open-File Rept., 99–522, http://geopubs.wr.usgs.gov/openfile/of99-522/of99-522.pdf, 1999.
Field, E. H., A summary of previous working groups on California earthquake probabilities, Bull. Seismol. Soc. Am., 97, 1033–1053, doi:10.1785/0120060048, 2007.
Field, E. H., T. E. Dawson, K. R. Felzer, A. D. Frankel, V. Gupta, T. H. Jordan, T. Parsons, M. D. Petersen, R. S. Stein, R. J. Weldon II, and C. J. Wills, Uniform California earthquake rupture forecast, version 2 (UCERF 2), Bull. Seismol. Soc. Am., 99, 2053–2107, doi:10.1785/0120080049, 2009.
Geographical Survey Institute, Crustal movements in the Tohoku district, Rep. Coord. Comm. Earthq. Predict., 83, 59–81, 2010 (in Japanese).
Igarashi, T., T. Matsuzawa, and A. Hasegawa, Repeating earthquakes and interplate aseismic slip in the northeastern Japan subduction zone, J. Geophys. Res., 108 (B5), 2249, doi:10.1029/2002JB001920, 2003.
Imamura, A., On the seismic activity of central Japan, Jpn. J. Astron. Geophys., 6, 119–137, 1928.
Jeffreys, H., Theory of Probability, third ed., 459 pp, Oxford Univ. Press, 1961.
Jolliffe, I. T. and D. B. Stephenson, eds., Forecast Verification, 240 pp, Chichester, England, John Wiley & Sons, 2003.
Jordan, T. H., Earthquake predictability, brick by brick, Seismol. Res. Lett., 77, 3–6, 2006.
Kagan, Y. Y. and D. D. Jackson, New seismic gap hypothesis: five years after, J. Geophys. Res., 100, 3943–3959, 1995.
Kelleher, J. A., Rupture zones of large South American earthquakes and some predictions, J. Geophys. Res., 77, 2087–2103, 1972.
Kelleher, J., L. Sykes, and J. Oliver, Possible criteria for predicting earthquake locations and their application to major plate boundaries of the Pacific and the Caribbean, J. Geophys. Res., 78, 2547–2585, 1973.
Matsuzawa, T., T. Igarashi, and A. Hasegawa, Characteristic small-earthquake sequence off Sanriku, northeastern Honshu, Japan, Geophys. Res. Lett., 29, 11, doi:10.1029/2001GL014632, 2002.
Matthews, M. V., W. L. Ellsworth, and P. A. Reasenberg, A Brownian model for recurrent earthquakes, Bull. Seismol. Soc. Am., 92, 2233–2250, 2002.
McCann, W. R., S. P. Nishenko, L. R. Sykes, and J. Krause, Seismic gaps and plate tectonics: Seismic potential for major boundaries, Pure Appl. Geophys., 117, 1082–1147, 1979.
Mishina, M., K. Tachibana, and S. Miura, Postseismic deformation associated with off Fukushima earthquakes as inferred data of borehole strain-meters, Geophys. Bull. Hokkaido Univ., 72, 287–298, 2009 (in Japanese with English abstract).
Nadeau, R. M., W. Foxall, and T. V. McEvilly, Clustering and periodic recurrence of microearthquakes on the San Andreas fault at Parkfield, California, Science, 267, 503–507, 1995.
Nagoya University, Source process of Off-Ibaraki earthquake on May 8, 2008 (Mj6.4, 7.0), Rep. Coord. Comm. Earthq. Predict, 80, 108–110, 2008 (in Japanese).
Nanjo, K. Z., T. Ishibe, H. Tsuruoka, D. Schorlemmer, Y. Ishigaki, and N. Hirata, Analysis of the completeness magnitude and seismic network coverage of Japan, Bull. Seismol. Soc. Am, 100 (6), 3261–3268, doi:10.1785/0120100077, 2010.
Nishenko, S. P., Circum-Pacific seismic potential: 1989–1999, Pure Appl. Geophys., 135, 169–259, 1991.
Okada, M., H. Takayama, F. Hirose, and N. Uchida, A prior distribution of the parameters in the renewal model with lognormal distribution used for estimating the probability of recurrent earthquakes, Zisin 2, 60, 85–100, 2007 (in Japanese with English abstract).
Rong, Y., D. D. Jackson, and Y. Y. Kagan, Seismic gaps and earthquakes, J. Geophys. Res., 108, 2471, doi:10.1029/2002JB002334, 2003.
Schorlemmer, D., M. C. Gerstenberger, S. Wiemer, D. D. Jackson, and D. A. Rhodes, Earthquake likelihood model testing, Seismol. Res. Lett., 78, 17–29, 2007.
Sykes, L. R., Aftershock zone of great earthquakes, seismicity gaps, and earthquake prediction for Alaska and the Aleutians, J. Geophys. Res., 76, 8021–8041, 1971.
Toth, Z., O. Talagrand, G. Candille, and Y. Zhu, Probability and ensemble forecasts, in Forecast Verification, a Practitiner’s Guide in Atmospheric Science, edited by Jolliffe and Stephenson, 137–163, John Wiley & Sons, 2003.
Uchida, N., T. Matsuzawa, A. Hasegawa, and T. Igarashi, Interplate quasi-static slip off Sanriku, NE Japan, estimated from repeating earthquakes, Geophys. Res. Lett., 30, 1801, doi:10.1029/2003GL017452, 2003.
Uchida, N., T. Matsuzawa, A. Hasegawa, and T. Igarashi, Recurrence intervals of characteristic M4.8+/−0.1 earthquakes off Kamaishi, NE Japan—Comparison with creep rate estimated from small repeating earthquake data, Earth Planet. Sci. Lett., 233, 155–165, 2005.
Uchida, N., M. Mishina, and T. Matsuzawa, Afterslip of the 2008 off Ibaraki (M7.0) and off Fukushima (M6.9) earthquakes estimated from small repeating earthquakes, ASC meeting, Tsukuba, November, 2008, Program & Abstracts, X-038, 210, 2008.
Uchida, N., J. Nakajima, A. Hasegawa, and T. Matsuzawa, What controls interplate coupling?: Evidence for abrupt change in coupling across a border between two overlying plates in the NE Japan subduction zone, Earth Planet. Sci. Lett., 283, 111–121, doi:10.1016/j.epsl.2009.04.003, 2009.
Wessel, P. and W. H. F. Smith, New version of the generic mapping tools released, Eos Trans. AGU, 76 (33), 329, 1995.
Wilks, S. S., Mathematical Statistics, 644 pp, John Wiley & Sons, 1962.
Working Group on California Earthquake Probabilities, Probabilities of large earthquakes occurring in California on the San Andreas fault, U.S. Geol. Surv., Open-File Rept., 88–398, 1988.
Working Group on California Earthquake Probabilities, Probabilities of large earthquakes in the San Francisco bay region, California, U.S. Geol. Surv, Circular 1053, 51 pp, 1990.
Working Group on California Earthquake Probabilities, Seismic hazards in southern California: probable earthquakes, 1994 to 2024, Bull. Seismol. Soc. Am., 85, 379–439, 1995.
Working Group on California Earthquake Probabilities, Earthquake probabilities in the San Francisco bay region: 2002–2031, U.S. Geol. Surv., Open-File Rept., 03-214, http://pubs.usgs.gov/of/2003/of03-214/, 2003.
Acknowledgements
We are indebted to two anonymous referees for helpful comments to suggest many improvements in the content and presentation of this report. We thank the members of the Research Center for Prediction of Earthquakes and Volcanic Eruptions, Tohoku University, for valuable discussions and suggestions. We are especially grateful to Prof. T. Matsuzawa, Drs. K. Nanjo, and H. Tsuruoka for their kind encouragement. The digital waveform data from the seismic stations of Hokkaido University, Tohoku University, and University of Tokyo were used in compiling the SRE catalog. We used the software coded by Mr. H. Takayama, which uses the GMT program package developed by Wessel and Smith (1995). The first author has been staying at the Meteorological Research Institute as a guest researcher and was helped by many members, especially Drs. Y. Hayashi, K. Maeda, A. Katsumata, M. Hoshiba, and S. Yoshikawa.
Author information
Authors and Affiliations
Corresponding author
Appendix A. Parameters in Inverse Gamma Prior Distribution Γ R (φ, ζ) for σ2
Appendix A. Parameters in Inverse Gamma Prior Distribution Γ R (φ, ζ) for σ2
The parameters of inverse gamma were given by Okada et al. (2007). We briefly mention here how to determine these parameters from observation data.
Suppose n random variables X
i
= ln(T
i
), i = 1, …, n obey a normal distribution N(µ, σ2) and take the variables for mean of n variables and sum of squared residual from mean,  and
and  , respectively. The variable Y/σ2 follows a chi-squared distribution with n − 1 degrees of freedom (e.g., Wilks, 1962) and Y obeys a gamma distribution Γ((n − 1)/2, 2σ2). Therefore the PDF of Y with a prior of π(σ2) is given as
, respectively. The variable Y/σ2 follows a chi-squared distribution with n − 1 degrees of freedom (e.g., Wilks, 1962) and Y obeys a gamma distribution Γ((n − 1)/2, 2σ2). Therefore the PDF of Y with a prior of π(σ2) is given as

If we adopt an inverse gamma prior distribution G R (ϕ,ζ) for σ2, the PDF for unbiased variance V = Y/(n − 1) is written as follow;

. Since the likelihood for Q sequences is defined as

where υ i of x i = ln(T i ) and n i are unbiased variance and the number of time interval data for the i-th sequence, respectively. Using the sequence unbiased variances of observed x i = ln(T i ) for many repeater sequences, we can estimate values of the parameters, ϕ and ζ, in inverse gamma prior distribution with a conventional maximum likelihood method.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Okada, M., Uchida, N. & Aoki, S. Statistical forecasts and tests for small interplate repeating earthquakes along the Japan Trench. Earth Planet Sp 64, 703–715 (2012). https://doi.org/10.5047/eps.2011.02.008
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.5047/eps.2011.02.008

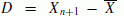 follows N (0,(n + 1)σ2n).
follows N (0,(n + 1)σ2n).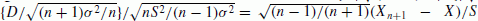 follows a t-distribution with n − 1 degrees of freedom.
follows a t-distribution with n − 1 degrees of freedom.












